《算法4》最短路径问题笔记

一、最短路径的定义：

在一幅加权有向图中，从顶点s到顶点t的最短路径是所有从s到t的路径中的权重最小者。

二、最短路径树

一幅加权有向图中，以s为起点的一颗最短路径树是图的一个子图，包含了s和从s可达的所有顶点。该有向树的根节点为s，树的每条路径都是有向图中的一条**最短路径。**即我们可以找到从s到达图中任何顶点的最短路径。

三、加权有向边

public class DirectedEdge {

    /**
     * 边的起点
     */
    private final int v;
    /**
     * 边的终点
     */
    private final int w;

    /**
     * 边的权重
     */
    private final double weight;

    public DirectedEdge(int v, int w, double weight) {
        this.v = v;
        this.w = w;
        this.weight = weight;
    }

    public double weight(){
        return weight;
    }
    public int from(){
        return v;
    }
    public int to(){
        return w;
    }

    @Override
    public String toString() {
        return String.format("%d->%d %.2f",v,w,weight);
    }
}

四、加权有向图

同前面讲图一样，我们在这里实现所需的加权有向图的类：

public class EdgeWeightedDigraph {
    private static final String NEWLINE = System.getProperty("line.separator");
	//顶点数
    private final int V;
    //边数
    private int E;
    //顶点v的入度
    private int[] indegree;             // indegree[v] = indegree of vertex v

    private Bag<DirectedEdge>[] adj;

    public EdgeWeightedDigraph(int v){
        this.V=v;
        this.E=0;
        this.adj=new Bag[V];
        this.indegree = new int[V];

        for (int i = 0; i < V; i++) {
            adj[i]=new Bag<>();
        }
    }
 
	//添加一条有向边
    public void addEdge(DirectedEdge edge) {
        int from = edge.from();
        validateVertex(from);
        int to = edge.to();
        validateVertex(to);
        adj[from].add(edge);
        indegree[to]++;
        E++;
    }
    //顶点v的邻边，即由v发出的边
    public Iterable<DirectedEdge> adj(int v) {
        validateVertex(v);
        return adj[v];
    }

    /**
     * 顶点v的出度
     * @param v
     * @return
     */
    public int outdegree(int v) {
        validateVertex(v);
        return adj[v].size();
    }

    /**
     * 顶点v的入度
     * @param v
     * @return
     */
    public int indegree(int v) {
        validateVertex(v);
        return indegree[v];
    }
    public int V() {
        return V;
    }
    public int E() {
        return E;
    }
	//返回所有的边
    public Iterable<DirectedEdge> edges(){
        Bag<DirectedEdge>bag=new Bag<>();
        for (int v = 0; v < V; v++) {
            for (DirectedEdge edge:adj[v]){
                bag.add(edge);
            }
        }
        return bag;
    }
    private void validateVertex(int v) {
        if (v < 0 || v >= V)
            throw new IllegalArgumentException("vertex " + v + " is not between 0 and " + (V-1));
    }
    public String toString() {
        StringBuilder s = new StringBuilder();
        s.append(V + " " + E + NEWLINE);
        for (int v = 0; v < V; v++) {
            s.append(v + ": ");
            for (DirectedEdge e : adj[v]) {
                s.append(e + "  ");
            }
            s.append(NEWLINE);
        }
        return s.toString();
    }
}

五、最短路径的数据结构

1. 最短路径树中的边
   和前面讲的DFS、BFS以及Prim算法一样，这里使用DirectedEdge[] edgeTo数组来保存最短路径树中的边。其中edgeTo[v] 表示 树中连接v和其父节点的边（也是从s到v的最短路径上的最后一条边）
2. 任意一个顶点v和起点s的距离
   使用edgeTo[] 数组保存起点s到任意顶点v的已知最短路径长度

同时做以下约定：
对于起点s： edgeTo[s]= null; distTo[s] =0.0
如果v从s不可达：distTo[v] = Double.POSITIVE_INFINITY

六、最短路径的求解思路

边的松弛

要想求得最短路径，每加入一个新的边，都必须对边进行“松弛”操作。
先看如下示例：

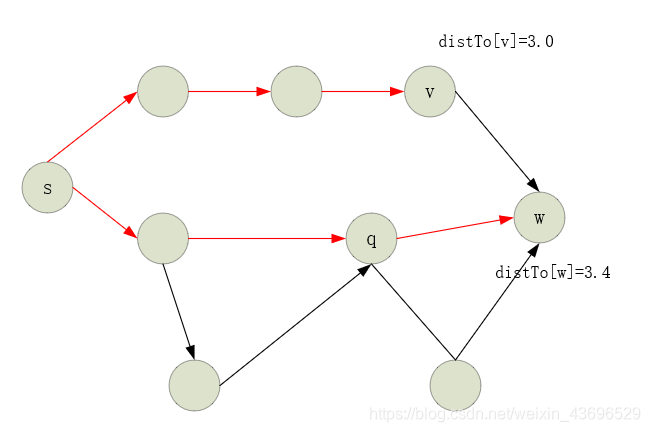
已知distTo[v] = 3.0，即从s到v的最短路径权重为3.0；而到w的最短路径为3.4
假设 待加入的新边 v -> w 的权重为0.2， 此时 distTo[v]+0.2 =3.2 小于原本distTo[w]=3.4，因此从s到w的最短路径应该经过v再到w，且权重为3.2

因此我们需要更新distTo[w]的值为 distTo[v]+0.2，这样才能得到一个更短的路径；并且更新edgeTo[w]=边v->w，此时边 q -> w 就不会再存放于最短路径树中，已经失效。

我们将如上的这样一个操作叫做对该边的一次成功的松弛(放松) 而如果distTo[v]加上边v->w的权重大于distTo[w]，则不做更新，它会让 边v->w 失效。
因此我们可以得到松弛的定义：

放松边v -> w意味着从s到w的最短路径是否是先从s到v，再从v到w。如果是，则根据该情况更新数据结构的内容。

由上我们可以得到通用的最短路径算法：
1.将distTo[s]初始化为0，其他顶点的distTo为无穷大
2.放松有向图中的任意一个边，直到不存在有效边为止

经过上述步骤，我们就可以保证对于任意一个从s可达的顶点w，distTo[w] 一定是从s到w的最短路径，且edgeTo[w] 为s到w的最短路径上的最后一条边。

七、Dijkstra（迪杰斯特拉）算法

有了上面的基础，我们再来引入最终解决最短路径的Dijkstra算法（其实上面已经说的差不多了）：
Dijkstra的思路跟Prim类似，但是Prim算法每次添加的都是距离树最近的非树顶点，而Dijkstra算法每次添加的是离起点s最近的非树顶点。

因此我们也需要借助索引优先队列来实现，将顶点v作为索引，从s到v的最短路径的权重值作为索引关联的值。

步骤如下：

1. 将distTo[s]初始化为0，数组的其他元素初始化为无穷大，并将s和distTo[s]加入索引优先队列；
2. 取出队列中优先级最高的索引（顶点），对从该顶点出发的邻边进行放松，并将放松成功的边的另一个顶点及其对应的distTo值加入到优先队列中（第一次访问到该点时，尚未将其加入到队列中，即distTo为无穷大）或更新优先队列中对应的值（该顶点新的distTo值比原来小）；
3. 当优先队列非空时，每次都取出一个索引（顶点），按2的方式进行放松，直到队列为空（即所有顶点都被加入到生成树中）

public class DijkstraSP {
    private DirectedEdge[] edgeTo;
    private  double[] distTo;
    /**
     * 索引优先队列：顶点v作为索引，从起点到v的最短路径的权值作为索引关联的对象
     */
    private IndexMinPQ<Double> pq;

    public DijkstraSP(EdgeWeightedDigraph digraph,int s){
        for (DirectedEdge e : digraph.edges()) {
            if (e.weight() < 0)
                throw new IllegalArgumentException("边 " + e + " 的权重为负值！");
        }
        edgeTo=new DirectedEdge[digraph.V()];
        distTo=new double[digraph.V()];
        pq=new IndexMinPQ<>(digraph.V());
        
        //初始化为无穷大
        for (int v = 0; v < digraph.V(); v++) {
            distTo[v]=Double.POSITIVE_INFINITY;
        }
        
        distTo[s]=0;

        pq.insert(s,0.0);
        while (!pq.isEmpty()){
            relax(digraph,pq.delMin());
        }
    }

    /**
     * 对顶点v的邻边放松
     * @param digraph
     * @param v
     */
    private void relax(EdgeWeightedDigraph digraph, int v) {
        for (DirectedEdge edge:digraph.adj(v)){
            int to=edge.to();

            if (distTo[to]>distTo[v]+edge.weight()){
                distTo[to]=distTo[v]+edge.weight();
                edgeTo[to]=edge;
                if (pq.contains(to)){
                    pq.changeKey(to,distTo[to]);
                }else {
                    pq.insert(to,distTo[to]);
                }
            }
        }
    }
}

因此，我们就可以解决如下几个问题：
1.该图的最短路径树；
2.从s到任意顶点v的最短路径
3.是否存在从s到v的最短路径，只要distTo[v] 非无穷大即存在。

    /**
     * 从起点到顶点v的最短路径权值
     * @param v
     * @return
     */
    public double distTo(int v){
        return distTo[v];
    }

    /**
     * 是否存在从s到v的最短路径
     * @param v
     * @return
     */
    public boolean hasPathTo(int v){
        return distTo[v]<Double.POSITIVE_INFINITY;
    }

    /**
     * 返回从s到v的最短路径
     * @param v
     * @return
     */
    public Iterable<DirectedEdge> pathTo(int v){
        if (!hasPathTo(v))return null;
        Stack<DirectedEdge> path=new Stack<>();
        for (DirectedEdge edge=edgeTo[v];edge!=null;edge=edgeTo[edge.from()])
        {
            path.push(edge);
        }
        return path;
    }

将Dijkstra算法稍作改动就可以实现任意顶点对之间的最短路径问题：

public class DijkstraAllPairsSP {
    private DijkstraSP[]all;


    public DijkstraAllPairsSP(EdgeWeightedDigraph digraph){
        all=new DijkstraSP[digraph.V()];
        for (int i = 0; i < digraph.V(); i++) {
            all[i]=new DijkstraSP(digraph,i);
        }
    }

    public Iterable<DirectedEdge> path(int s,int t){
        return all[s].pathTo(t);
    }
    public double distBetween(int s,int t){
        return all[s].distTo(t);
    }
}

Dijkstra算法适用于加权有向非负权值的单起点图的最短路径问题，有环无环都不影响正确性。

八、无环加权有向图中的最短路径算法

许多应用中的加权有向图都是不含有有向环的，因此我们介绍一个基于无环的加权有向图的最短路径算法，该算法比Dijkstra算法要快，能够在线性时间内解决该问题，且能够处理负权值的边，并找出最长路径。

该算法的思想是：

按照图的拓扑排序一个个放松所有的顶点，就能在和E+V成正比的时间内解决无环加权有向图的单点最短路径问题。

证明如下：
每条边v->w只会被放松一次。因为顶点v被放松时，distTo[w]<=distTo[v]+e.weight()，在算法结束前，该不等式始终成立。因为我们是按照拓扑排序放松顶点，所以v被放松后，就不会处理任何指向v的边，而distTo[w]的值只能变小。

实现如下：

public class AcyclicSP {
    private DirectedEdge[] edgeTo;
    private double[] distTo;
    public AcyclicSP(EdgeWeightedDigraph digraph,int s){
        edgeTo=new DirectedEdge[digraph.V()];
        distTo=new double[digraph.V()];

        for (int v=0;v<digraph.V();v++){
            distTo[v]=Double.POSITIVE_INFINITY;
        }
        distTo[s]=0.0;
		//先求出拓扑排序
        TopologicalSort sort=new TopologicalSort(digraph);
        if (!sort.hasOrder()){
            throw new IllegalArgumentException("Digraph is not acyclic.");
        }
        //按照拓扑排序放松顶点
        for(int v:sort.order()){
            relax(digraph,v);
        }
    }

    private void relax(EdgeWeightedDigraph digraph, int v) {
        for (DirectedEdge edge:digraph.adj(v)){
            int to=edge.to();
            if (distTo[to]>distTo[v]+edge.weight()){
                distTo[to]=distTo[v]+edge.weight();
                edgeTo[to]=edge;
            }
        }
    }
    public double distTo(int v){
        return distTo(v);
    }
    public boolean hasPathTo(int v){
        return distTo(v)<Double.POSITIVE_INFINITY;
    }

    public Iterable<DirectedEdge> pathTo(int v){
        Stack<DirectedEdge> path=new Stack<>();
        for ( DirectedEdge edge=edgeTo[v]; edge!=null ; edge=edgeTo[edge.from()]) {
            path.push(edge);
        }
        return path;
    }
}

如果我们对上述算法稍作修改，即将distTo的初始值设为无穷小，将放松时distTo[w]><distTo[v]+edge.weight()的条件修改为distTo[w]<distTo[from]+edge.weight()，就可以实现无环加权有向图中的单点最长路径：

/**
 * 加权有向无环图的最长路径
 * @author MaoLin Wang
 * @date 2020/2/2416:38
 */
public class AcyclicLP {
    private double[] distTo;
    private DirectedEdge[] edgeTo;

    public AcyclicLP(EdgeWeightedDigraph digraph,int s) {
        distTo=new double[digraph.V()];
        edgeTo=new DirectedEdge[digraph.V()];

        for (int i = 0; i < digraph.V(); i++) {
        	//初始化为无穷小
            distTo[i]=Double.NEGATIVE_INFINITY;
        }
        distTo[s]=0.0;
        TopologicalSort sort=new TopologicalSort(digraph);
        if (sort.order()==null){
            throw new IllegalArgumentException("参数错误");
        }
        for (int w:sort.order()){
            relax(digraph,w);
        }
    }

    private void relax(EdgeWeightedDigraph digraph, int v) {
        for (DirectedEdge edge:digraph.adj(v)){
            int to=edge.to(),from = edge.from();
            if (distTo[to]<distTo[from]+edge.weight()){ //修改为<
                distTo[to]=distTo[from]+edge.weight();
                edgeTo[to]=edge;
            }
        }
    }
    public double distTo(int v) {
        return distTo[v];
    }


    public boolean hasPathTo(int v) {
        return distTo[v] > Double.NEGATIVE_INFINITY;
    }

    public Iterable<DirectedEdge> pathTo(int v){
        if (!hasPathTo(v)){
            return null;
        }
        Stack<DirectedEdge> path=new Stack<>();
        for (DirectedEdge edge=edgeTo[v];edge!=null;edge=edgeTo[edge.from()]){
            path.push(edge);
        }
        return path;
    }
}

九、一般加权有向图中的最短路径算法

该算法解决既可能含有环，也可能含有负权值边的加权有向图的最短路径算法。

这个仅做记录吧，可能个人讲的不太明白。

解决该问题的算法试Bellman-Ford算法，实现如下：

/**
 * 基于队列的Bellman-Ford算法
 * 在任意含有V个顶点的加权有向图中给定起点s，从s无法到达任何负权重环
 * 将distTo[s]初始化为0，其他distTo[]元素为无穷大，以任意顺序放松有向图的所有边，重复V轮
 * @author MaoLin Wang
 * @date 2020/2/2421:41
 */
public class BellmanFordSP {

    private double[] distTo;
    private DirectedEdge[] edgeTo;

    /**
     * 该顶点是否在队列中
     */
    private boolean[] onQ;
    /**
     * 正在被放松的顶点
     */
    private Queue<Integer> queue;

    /**
     * relax()的调用次数
     */
    private int cost;

    /**
     * edgeTo[]中是否有负权重环
     */
    private Iterable<DirectedEdge> cycle;

    public BellmanFordSP(EdgeWeightedDigraph digraph,int s) {
        distTo=new double[digraph.V()];
        edgeTo=new DirectedEdge[digraph.V()];
        onQ=new boolean[digraph.V()];
        queue=new Queue<>();

        for (int v = 0; v < digraph.V(); v++) {
            distTo[v]=Double.POSITIVE_INFINITY;
        }
        distTo[s]=0.0;
        queue.enqueue(s);
        onQ[s]=true;

        while (!queue.isEmpty() && !hasNegativeCycle()){
            int v=queue.dequeue();
            onQ[v]=false;
            relax(digraph,v);
        }
    }

    private void relax(EdgeWeightedDigraph digraph, int v) {
        for (DirectedEdge edge:digraph.adj(v)){
            int to=edge.to();
            if (distTo[to]>distTo[v]+edge.weight()){
                distTo[to]=distTo[v]+edge.weight();
                edgeTo[to]=edge;
                if (!onQ[to]){
                    queue.enqueue(to);
                    onQ[to]=true;
                }
            }
            //调用V次relax后查找负权重环
            if (cost++ % digraph.V()==0){
                findNegativeCycle();
            }
        }
    }

    /**
     * 查找负权重环，没有则返回null
     */
    private void findNegativeCycle() {
        int V=edgeTo.length;
        EdgeWeightedDigraph digraph;
        digraph=new EdgeWeightedDigraph(V);
        for (int v = 0; v < V; v++) {
            if (edgeTo[v]!=null){
                digraph.addEdge(edgeTo[v]);
            }
        }
        EdgeWeightedDirectedCycle directedCycle;
        directedCycle=new EdgeWeightedDirectedCycle(digraph);
        cycle=directedCycle.cycle();

    }

    /**
     * 是否含有负权重环
     * @return
     */
    public boolean hasNegativeCycle() {
        return cycle!=null;
    }

    public Iterable<DirectedEdge> negativeCycle(){
        return cycle;
    }
    public boolean hasPathTo(int v){
        return distTo[v]<Double.POSITIVE_INFINITY;
    }
    public double distTo(int v){
        return distTo[v];
    }
    public Iterable<DirectedEdge> pathTo(int v){
        if (hasNegativeCycle())
            throw new UnsupportedOperationException("Negative cost cycle exists");
        if (!hasPathTo(v)) return null;
        Stack<DirectedEdge> path = new Stack<DirectedEdge>();
        for (DirectedEdge e = edgeTo[v]; e != null; e = edgeTo[e.from()]) {
            path.push(e);
        }
        return path;
    }

   

}