1 隐马尔科夫模型

本文主要介绍NLP领域中很重要的一个模型——隐马尔科夫模型（Hidden Markov Model，HMM）。希望读完本文后，大家能够清楚地理解HMM并能够应用到实际中。

隐马尔科夫模型是结构最简单的动态贝叶斯网（dynamic Bayesian network，也被称作有向图模型），HMM是可以用于标注问题的统计数学模型，描述由隐藏的马尔科夫链随机生成观测序列的过程，属于生成模型。HMM模型在语音识别、自然语言处理、生物信息、模式识别等领域有广泛的应用。

1.1 HMM解决的问题

首先看看什么样的问题可以使用HMM模型解决。

使用HMM模型来解决的问题一般有两个特征：

1）问题是基于序列的，比如时间序列、状态序列。
2 ）问题中有两类数据，一类序列数据是可以观测到的，即观测序列；而另一类数据是不能观察到的，即隐藏状态序列，简称状态序列。

如果问题有了这两个特征，那么这个问题一般可以使用HMM模型尝试解决，这样的问题在生活中是很多的。例如，说一句话，发出的声音是观测序列，想表达的意思是隐藏状态序列；写文章的过程可以想象为先在脑海中构思好一个满足语法的词性序列，然后再将每个词性填充为具体的词语。

1.2 HMM模型的定义

隐马尔科夫模型是关于时序的概率模型，描述由一个隐藏的马尔科夫链随机生成不可观测的状态随机序列，再由各个状态生成一个观测而产生观测随机序列的过程（摘自《统计学习方法》）。隐藏的马尔科夫链随机生成的状态的序列，称为状态序列（state sequence），记作 $\boldsymbol{y}$ ；每个状态生成一个观测，而由此产生的观测的随机序列，称为观测序列（observation sequence），记作 $\boldsymbol{x}$ 。序列的每一个位置又可以看作一个时刻。
HMM模型示意图

HMM模型示意图

1.2.1HMM的两个假设

首先介绍一下马尔科夫假设：每个事件的发生概率只取决于前一个事件。将满足该假设的连续多个事件串联在一起，就构成了马尔科夫链。在NLP语境下，可以将事件具象为单词，于是马尔科夫模型就是二元语法。

第一个假设：将马尔科夫假设作用于状态序列，假设当前状态 $y_t$ 仅仅依赖于前一个状态 $y_{t-1}$ ，连续多个状态构成隐马尔科夫链 $\boldsymbol{y}$ 。数学表达式为：
$p(y_t|y_{t-1},x_{t-1},y_{t-2},x_{t-2},y_{t-3},x_{t-3},...,y_{1},x_1)=p(y_t|y_{t-1}), t=1,2,3,...,T$

有了隐马尔科夫链，如何建立与观测序列 $\boldsymbol{x}$ 的联系呢？HMM做了第二个假设:

第二个假设：任意时刻的观测 $x_t$ 只依赖于该时刻的状态 $y_t$ ，与其他时刻的状态或观测独立无关。数学表达式为：
$p(x_t|y_T,x_T,y_{t-1},x_{t-1},...,y_{t+1},x_{t+1},y_t,y_{t-1},x_{t-1},...y_1,x_1)=p(x_t|y_t),t=1,2,3,...,T$

1.2.2 HMM模型

设 $Q$ 是所有可能的状态的集合， $V$ 是所有可能的观测的集合。
$Q=\{q_1,q_2,...,q_N\}，V=\{v_1,v_2,v_3,...,v_N\}$
其中，N是可能的状态数，M是可能的观测数。
HMM模型用三元组来表示 $\lambda=(\boldsymbol{\pi},A,B)$ ：

$\boldsymbol{\pi}$ : 初始状态概率向量
A：状态转移概率矩阵
B：发射概率矩阵

系统怎么从零开始呢？ 观测值是由隐藏状态产生的，所以系统最初应该是生成隐藏状态。

初始概率向量指的是系统启动时进入的第一个状态 $y_1$ 成为初始状态， $\boldsymbol{y}$ 有 $N$ 种取值，从 $Q$ 集合中选取一个，即 $\boldsymbol{y} \in \{q_1,q_2,...,q_N\}$ 。由于 $y_1$ 是第一个状态，是一个独立的离散随机变量，可以用 $p(y_1|\boldsymbol{\pi})$ 来描述， $y_1$ 只由 $\boldsymbol{\pi}$ 来控制，其中 $\boldsymbol{\pi}=(\pi_1,\pi_2,\pi_3,...,\pi_N)^T,0\leq\pi_i\leq1,\sum\limits^{N}_{i=1}{\pi_i}$ =1。 $\boldsymbol{\pi}$ 是概率分布的参数向量，称为初始状态概率向量。给定 $\boldsymbol{\pi}$ ，初始状态 $y_1$ 的取值分布就确定了。以中文分词问题为例，采用{B,M,E,S}标记时，其中B代表一个词的第一个字，M代表词的中间字，E代表词的末尾字，S代表单字成词。 $y_1$ 所有可能的取值及对应的概率如下：

$p(y_1=B)=0.7$

$p(y_1=M)=0$

$p(y_1=E)=0$

$p(y_1=s)=0.3$

则 $\pi=[0.7,0,0,0.3]$ ，也就是说句子第一个字可能是一个单字或者一个词的首字，不可能是一个词的中间或者尾字。

$y_1$ 确定之后，怎么产生 $x_1$ 呢？如何确定 $x_1$ 的概率分布呢？

根据第二个假设：当前观测值 $x_1$ 仅取决于当前的状态 $y_1$ ，对于从 $Q$ 中取出的每一种状态 $y_1$ ， $x_1$ 都可以从 $V$ 集合中的 $M$ 个值选一个，所以对于每一个 $y,x$ 都是一个独立的离散随机变量，其概率参数对应一个向量，维度为 $M$ ，即 $\boldsymbol{x} \in \{v_1,v_2,...,v_N\}$ 。由于一共有 $N$ 种 $y$ ，所以这些向量构成了一个 $N\times M$ 矩阵，称为发射概率矩阵 $\boldsymbol{B}$ 。
$\boldsymbol{B}=[b_{ij}]_{N\times M}=[p(x_t=v_i|y_t=q_j)]_{N\times M}$

其中， $p(x_t=v_i|y_t=q_j)$ 代表t时刻，隐藏状态 $y_t$ 是 $q_j$ ，由这个状态产生的观测值 $x_t$ 等于 $v_i$ 的概率。

状态	观测值1	观测值2	…	观测值M
状态1
状态2
…
状态N

发射概率矩阵是一个非常形象的术语：可以将 $\boldsymbol{y}$ 想象成为不同的彩弹枪， $\boldsymbol{x}$ 为不同颜色的子弹，每把彩弹枪内的颜色子弹比例不一样，导致有的彩弹枪红色子弹较多比较容易发射红色彩弹，一些彩弹枪绿色子弹较多更容易发射绿色彩弹。
发射概率在中文分词中也具有实际意义，有些字符构词的位置比较固定，比如一把作为词首的枪，不容易发射出“餮”，因为“餮”一般作为“饕餮”的词尾出现。通过给 $p(x_1=餮|y_1=B)$ 较低的概率，HMM模型可以有效的防止“饕餮”被错误的切分。

$y_1$ 确定之后，如何转移状态到 $y_2$ ?乃至 $y_n$ ？

根据HMM模型的第一个假设： $t+1$ 时刻的状态仅仅取决于 $t$ 时刻的状态。类似发射概率矩阵，对于 $t$ 时刻的每一种状态， $y_{t+1}$ 是一个离散的随机变量，取值有 $N$ 种。 $t$ 时刻一共可能有 $N$ 种状态，所以从 $t$ 时刻到 $t+1$ 时刻的状态转移矩阵为 $N\times N$ 的方阵，称为状态转移概率矩阵 $\boldsymbol{A}$ :
$\boldsymbol{A}=[a_{ij}]_{N\times N}=[p(y_{t+1}=v_j|y_t=v_i)]_{N\times N}$

其中， $p(y_{t+1}=s_j|y_t=s_i)$ 表示 $t$ 时刻的状态为 $v_i$ ， $t+1$ 时刻的状态为 $v_j$ 的概率。

当前状态	下一状态是状态1	状态2	…	状态N
状态1
状态2
…
状态N

例如，在中文分词中，标签B后面不可能是S，于是给 $p(y_{t+1}=S|y_t=B)=0$ 就可以防止B后面接S的情况出现。

初始状态概率向量、状态转移概率矩阵与发射概率矩阵称为HMM模型的三元组 $\lambda=(\boldsymbol{\pi},A,B)$ ，只要三元组确定了，HMM模型就确定了。

举一个经典的例子：
假设有四个盒子，每个盒子里都装有红白两种颜色的球，如下表：

盒子	1	2	3	4
红球数	5	3	6	8
白球数	5	7	4	2

盒子示意
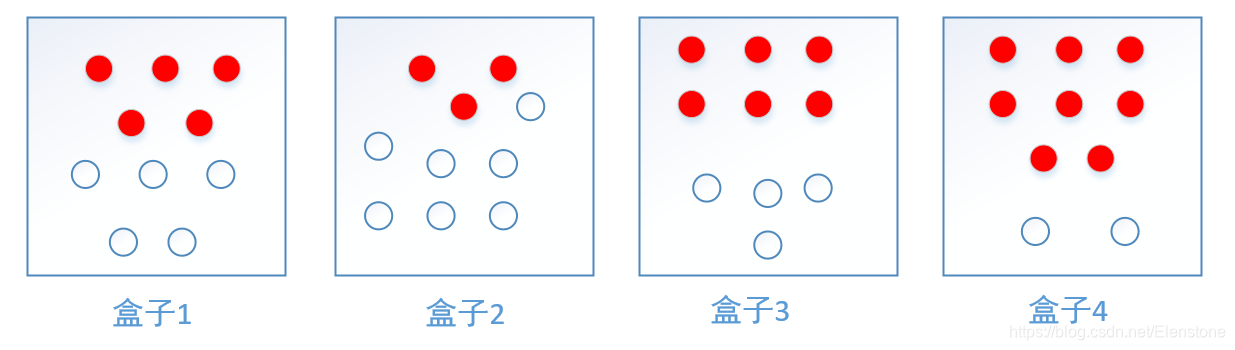
按照下面的方法抽球，产生一个球的颜色观察序列：

从4个盒子里以等概率随机选取一个盒子，从这个盒子里随机抽取一个球，记录颜色后，放回；
从当前盒子随机转移到下一个盒子，规则是：如果当前盒子是盒子1，那么下一个盒子一定是盒子2，如果当前是盒子2或者3，那么分别以概率0.4和0.6转移到左边或右边的盒子，如果当前盒子是4，那么各以0.5的概率停留在盒子4或者转移到盒子3；
确定转移盒子后，再从这个盒子里随机抽取一个球，记录其颜色，放回；
重复2,3步骤3次

一共抽取出来5个球，得到一个球的颜色观察序列：
$\boldsymbol{x}=\{\color{red}红，红，\color{black}白，白，\color{red}红\}$

在这个过程中，观察者只能观测到球的颜色序列，观测不到球是从哪个盒子取出的，即观察不到盒子的序列。
这个例子中有两个随机序列，一个是盒子的序列（状态序列），一个是球的颜色的观测序列（观测序列），前者是隐藏的，后者是可以观测的。根据所给的条件可以明确状态集合、观测集合、序列长度以及模型的三要素。

状态集合是 $Q=\{盒子1，盒子2，盒子3，盒子4\}，N=4$ 。
观测集合是 $V=\{\color{red}红，\color{black}白\}$ 。
状态序列和观测序列的长度 $T=5$ ，原因是一共观测了5次。
初始状态概率向量为 $\boldsymbol{\pi}=(0.25,0.25,0.25,0.25)^T$ ，原因是第一次是等概率随机抽取一个盒子。
状态转移概率矩阵 $A=\begin{bmatrix} 0 & 1 & 0 & 0 \\ 0.4 & 0 & 0.6 & 0\\ 0 & 0.4 & 0 &0.6\\ 0 & 0 & 0.5 & 0.5 \end{bmatrix}$
发射概率矩阵 $B=\begin{bmatrix} 0.5 & 0.5 \\ 0.3 & 0.7 \\ 0.6 & 0.4 \\ 0.8 & 0.2 \\ \end{bmatrix}$

1.3 HMM模型的三个基本问题

有了HMM模型之后，如何使用模型呢？HMM模型一个可以解决三个问题：

概率计算问题：给定模型参数 $\lambda=(\boldsymbol{\pi},A,B)$ ，和一个观测序列 $\boldsymbol{x}$ ,，计算在这个模型参数 $\lambda$ 下，观测序列出现的最大概率，即 $p(\boldsymbol{x}|\lambda)$ 的最大值。
模型训练问题：给定训练集 $(\boldsymbol{x}^{(i)},\boldsymbol{y}^{(i)})$ ，估计模型参数 $\lambda=(\boldsymbol{\pi},A,B)$ ，使得在该模型下观测序列概率 $p(\boldsymbol{x}|\lambda)$ 最大，即使用极大似然估计得方法估计参数。
序列预测问题：也称为解码问题，已知模型参数 $\lambda=(\boldsymbol{\pi},A,B)$ ，给定观测序列 $\boldsymbol{x}$ ，求最有可能的状态序列 $\boldsymbol{y}$ ，即求 $p(\boldsymbol{y}|\boldsymbol{x})$ 的最大值。

2 概率计算问题及算法

概率计算问题，也就是在给定的模型参数三元组的条件生成观测序列的过程。给定模型参数 $\lambda=(\boldsymbol{\pi},A,B)$ 和一个观测序列 $\boldsymbol{x}$ ,，计算在这个模型参数 $\lambda$ 下，观测序列出现的最大概率，即 $p(\boldsymbol{x}|\lambda)$ 的最大值。先介绍概念上可行但计算上不行的直接计算法（暴力解法），然后介绍前向算法与后向算法。

2.1 直接计算法

给定模型参数 $\boldsymbol{\lambda}=(\boldsymbol{\pi},A,B)$ 和一个观测序列 $\boldsymbol{x}=\{x_1,x_2,x_3,...x_T\}$ ，计算观测序列出现的概率 $p(\boldsymbol{x}|\lambda)$ ，最直接的方法就是按照概率公式直接计算，通过列举所有可能的长度为 $T$ 的状态序列 $\boldsymbol{y}=\{y_1,y_2,y_3,...,y_T\}$ ，求各个状态序列 $\boldsymbol{y}$ 与观测序列 $\boldsymbol{x}=(x_1,x_2,x_3,...,x_T)$ 的联合概率 $p(\boldsymbol{x},\boldsymbol{y}|\boldsymbol{\lambda})$ ,，然后对所有可能的状态序列求和，得到 $p(\boldsymbol{x}|\boldsymbol{\lambda})$ 。
状态序列 $\boldsymbol{y}=(y_1,y_2,y_3,...,y_T)$ 发生的概率是：
$p(\boldsymbol{y}|\boldsymbol{\lambda})=\pi_{y_1}a_{y_1y_2}a_{y_2y_3}...a_{y_{T-1}y_T}$

对固定的状态序列 $\boldsymbol{y}=(y_1,y_2,y_3,...,y_T)$ 并且观测序列为 $\boldsymbol{x}=(x_1,x_2,x_3,...,x_T)$ 的概率是：
$p(\boldsymbol{x}|\boldsymbol{y},\boldsymbol{\lambda})=b_{y_1x_1}b_{y_2x_2}b_{y_3x_3}...b_{y_Tx_T}$

在给定HMM模型参数 $\boldsymbol{\lambda}$ 的条件下， $\boldsymbol{x},\boldsymbol{y}$ 同时出现的联合概率为：
$\begin{aligned}p(\boldsymbol{x},\boldsymbol{y}|\boldsymbol{\lambda})&=p(\boldsymbol{x}|\boldsymbol{y},\boldsymbol{\lambda})p(\boldsymbol{y}|\boldsymbol{\lambda})\\ &=\pi_{y_1}b_{y_1x_1}a_{y_1y_2}b_{y_2x_2}a_{y_2y_3}b_{y_3x_3}...a_{y_{T-1}y_T}b_{y_Tx_T} \end{aligned}$

然后，对所有可能的状态序列 $\boldsymbol{y}$ 求和，得到观测序列 $\boldsymbol{x}$ 的概率 $p(\boldsymbol{x}|\lambda)$ ，即：
$\begin{aligned} p(\boldsymbol{x}|\lambda)&=\sum\limits_\boldsymbol{y}p(\boldsymbol{x},\boldsymbol{y}|\boldsymbol{\lambda})\\ &=\sum\limits_\boldsymbol{y}p(\boldsymbol{x}|\boldsymbol{y},\boldsymbol{\lambda})p(\boldsymbol{y}|\boldsymbol{\lambda})\\ &=\sum\limits_{y_1,y_2,y_3,...,y_T}\pi_{y_1}b_{y_1x_1}a_{y_1y_2}b_{y_2x_2}a_{y_2y_3}b_{y_3x_3}...a_{y_{T-1}y_T}b_{y_Tx_T} \end{aligned}$

利用这个公式计算量很大，复杂度是 $O(TN^T)$ ，在实际中是不可行的。

2.2 前向算法

首先需要定义前向概率：给定HMM模型 $\boldsymbol{\lambda}$ ，定义时刻 $t$ 部分观测序列为 $\boldsymbol{x}=(x_1,x_2,x_3,...,x_t)$ 且状态为 $q_i$ 的概率为前向概率，记作：
$\alpha_t(i)=p(x_1,x_2,x_3,...,x_t,y_t=q_i|\boldsymbol{\lambda})$

前向算法：

输入：HMM模型参数 $\boldsymbol{\lambda}$ ，观测序列 $\boldsymbol{x}=(x_1,x_2,x_3,...,x_t)$ ；
输出：观测序列概率 $p(\boldsymbol{x}|\boldsymbol{\lambda})$ 。

算法步骤：

初始：
根据 $\boldsymbol{\pi}$ 生成 $t=1$ 时刻的状态 $y_1=q_i$ ，概率为 $\pi_i$ ，并且根据发射概率矩阵 $\boldsymbol{B}$ 由 $y_1=q_i$ 生成 $x_1$ ，概率为 $b_{ix_1}$ ，则：
$\alpha_1(i)=\pi_ib_{ix_1}$
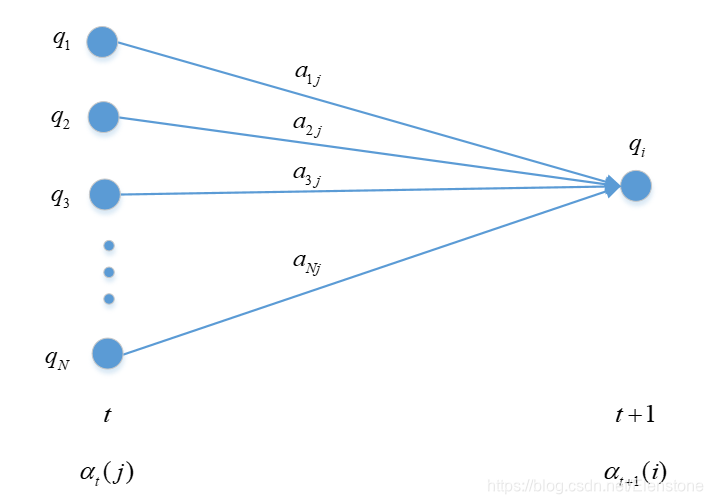
递推：
当 $t=2$ 时，根据状态转移概率矩阵 $\boldsymbol{A}$ ，系统的状态由 $y_1=q_j$ 变为 $y_2=q_i$ ，概率为 $a_{ji}$ ， $p(y_2=q_i,y_1=q_j,x_1|\boldsymbol{\lambda})=\alpha_1(j)a_{ji}$ 。不管 $y_1$ 为什么状态，都可能转移到状态 $y_2=q_i$ ，所以需要对 $y_1$ 求和: $\sum\limits_{j=1}^N\alpha_1(j)a_{ji}$ 。根据 $\alpha_t(i)$ 的定义， $t=2$ 时刻，由状态 $y_2=q_i$ 产生观测值 $x_2$ 的概率为 $b_{ix_2}$ ，所以：
$\alpha_2(i)=[\sum\limits_{j=1}^N\alpha_1(j)a_{ji}]b_{ix_2}$

对 $t=1,2,3,...T-1$ ，有：
$\alpha_{t+1}(i)=[\sum\limits^N_{j=1}\alpha_t(j)a_{ji}]b_{ix_{t+1}},\quad i=1,2,3,...N$
在这里插入图片描述
3. 终止：
时刻 $t=T$ ：
根据定义可知： $\alpha_T(i)$ 表示， $t=T$ 时刻，处于状态 $y_T=q_i$ ，并且观察到的序列为 $\boldsymbol{x}=(x_1,x_2,x_3,...,x_T)$ 的概率：
$\begin{aligned} \alpha_T(i)&=p(x_1,x_2,x_3,...,x_T,y_T=q_i|\boldsymbol{\lambda})\\ &=p(\boldsymbol{x},y_T=q_i|\boldsymbol{\lambda}) \end{aligned}$

所以：

$p(\boldsymbol{x}|\boldsymbol{\lambda})=\sum\limits^N_{i=1}\alpha_T(i)$

前向算法实际是基于“状态序列的路径结构”递推计算 $p(\boldsymbol{x}|\boldsymbol{\lambda})$ 的算法。前向算法高效的关键是其局部计算前向概率，然后利用路径结构将前向概率递推到全局，得到 $p(\boldsymbol{x}|\boldsymbol{\lambda})$ 。在 $t=1$ 时刻计算 $\alpha_1(i)$ 的 $N$ 个值，而当 $t\geq2$ 时，计算每一个\alpha_t(i)的值都会利用前 $N$ 个 $\alpha_{t-1}(i)$ 的值，减少计算量的原因在于每一次计算都直接引用前一个时刻的计算结果，避免了概率的重复计算，复杂度为 $O(N*N*T)$ ，而不是直接算法的 $O(TN^T)$ 。

例：上文中的盒子和球模型，状态集合为 $Q=\{1,2,3\}$ ，观测集合为 $V=\{红，白\}$ ，
$A=\begin{bmatrix} 0.5 & 0.2 & 0.3\\ 0.3 & 0.5 & 0.2\\ 0.2 & 0.3 & 0.5 \end{bmatrix}$ ， $B=\begin{bmatrix} 0.5 & 0.5 \\ 0.4 & 0.6\\ 0.7 & 0.3 \end{bmatrix}$ ， $\pi=(0.2,0.4,0.4)^T$
设 $T=3$ ， $\boldsymbol{x}=(红，白，红)$ ，用前向算法来计算 $p(\boldsymbol{x}|\boldsymbol{\lambda})$ 。
解：

计算初值：
$\alpha_1(1)=\pi_1b_{1x_1}=0.2\times0.5=0.10$

$\alpha_1(2)=\pi_2b_{2x_1}=0.4\times0.4=0.16$

$\alpha_1(3)=\pi_3b_{3x_1}=0.4\times0.7=0.28$
2. 递推计算：
$\alpha_2(1)=[\sum\limits_{i=1}^3\alpha_1(i)a_{i1}]b_{1x_2}=[0.10\times0.5+0.16\times0.3+0.28\times0.2)]\times0.5=0.077$

$\alpha_2(2)=[\sum\limits_{i=1}^3\alpha_1(i)a_{i2}]b_{2x_2}=[0.10\times0.2+0.16\times0.5+0.28\times0.3)]\times0.5=0.1104$

$\alpha_2(3)=[\sum\limits_{i=1}^3\alpha_1(i)a_{i3}]b_{3x_2}=[0.10\times0.3+0.16\times0.2+0.28\times0.5)]\times0.5=0.0606$

$\alpha_3(1)=[\sum\limits_{i=1}^3\alpha_2(i)a_{i1}]b_{1x_3}=0.04187$

$\alpha_3(2)=[\sum\limits_{i=1}^3\alpha_2(i)a_{i2}]b_{2x_3}=0.03551$

$\alpha_3(3)=[\sum\limits_{i=1}^3\alpha_2(i)a_{i3}]b_{3x_3}=0.05284$

终止：

$p(\boldsymbol{x}|\boldsymbol{\lambda})=\sum\limits_{i=1}^3\alpha_3(i)=0.13022$

2.3 后向算法

类似前向算法，定义：给定HMM模型 $\boldsymbol{\lambda}$ ，定义时刻 $t$ 状态为 $q_i$ 的条件下，从 $t+1到T$ 的部分观测序列为 $x_{t+1},x_{t+2},x_{t+3},...,x_T$ 的概率为后向概率，记作：
$\beta_t(i)=p(x_{t+1},x_{t+2},x_{t+3},...,x_T|y_t=q_i,\boldsymbol{\lambda})$
后向算法：

输入：HMM模型参数 $\boldsymbol{\lambda}$ ，观测序列 $\boldsymbol{x}=(x_1,x_2,x_3,...,x_t)$ ；
输出：观测序列概率 $p(\boldsymbol{x}|\boldsymbol{\lambda})$ 。

当 $t=T$ 时:
$\beta_T(i)=p(这里没东西|y_T=q_i,\boldsymbol{\lambda})=1$
这里可以这么理解：按理说好需要看看T时刻过后是什么观测值，但是T时刻之后没有观测值了，不管T时刻状态是什么，之后就是没有观测值，所以没有观测值的概率为1，且与状态无关。
对 $t=T-1$ :
已知 $\beta_T(j)$ ，根据HMM模型可知， $y_T=q_j$ 是由 $y_{T-1}$ 转移而来的，假设 $y_{T-1}=q_i$ ，转移的概率为 $a_{ij}$ :
根据 $\beta_{T-1}(i)$ 的定义，时刻 $T-1$ 的状态 $y_{T-1}=q_i$ ，从T到T的观测序列为 $x_T$ ，T时刻状态 $y_T=q_j$ 生成 $x_T$ 的概率为 $b_{jx_T}$ ，则：
$\beta_{T-1}(i)=\sum\limits^N_{j=1}a_{ij}b_{jx_T}\beta_T(j)$
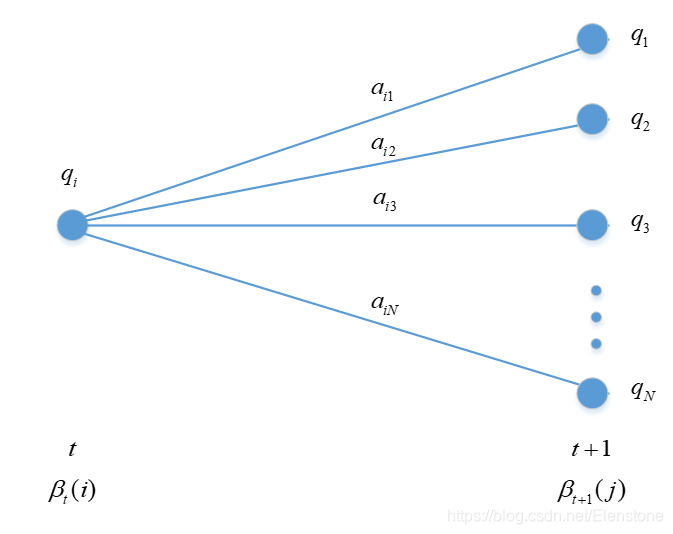
对 $t=T-1,T-2,...,1$ :
$b_{jx_t}=p(x_t|y_t=q_j,\boldsymbol{\lambda}))$

$a_{ij}=p(y_{t+1}=q_j|y_t=q_i,\boldsymbol{\lambda}))$

$\beta_{t+1}(j)=p(x_{t+2},x_{t+3},...,x_T|y_{t+1}=q_j,\boldsymbol{\lambda})$

由状态 $y_{t+1}=q_j$ 生成 $t+1$ 时刻的观测值 $x_{t+1}$ :
$\begin{aligned} b_{jx_{t+1}}\beta_{t+1}(j)&=p(x_{t+1}|y_{t+1}=q_j,\boldsymbol{\lambda})p(x_{t+2},x_{t+3},...,x_T|y_{t+1}=q_j,\boldsymbol{\lambda})\\ &=p(x_{t+1},x_{t+2},...,x_T|y_{t+1}=q_j,\boldsymbol{\lambda})\end{aligned}$

按照条件概率来理解：在 $t+1$ 时刻状态为 $y_{t+1}=q_j$ 的条件下，观察到 $x_{t+1},x_{t+2},...,x_T$ 的概率为 $b_{jx_{t+1}}\beta_{t+1}(j)$ ，由于 $\beta_t(i)$ 与 $t$ 时刻的状态 $y_t$ 有关，根据HMM模型的第一个假设， $y_{t+1}$ 仅仅与 $y_t$ 有关，且概率 $a_{ij}$ 由状态转移矩阵矩阵A提供。 $\beta_t(i)$ 表示在 $t$ 时刻状态为 $y_t=q_i$ 的条件下，观察到 $x_{t+1},x_{t+2},...,x_T$ 的概率，这个概率若要用 $\beta_{t+1}(j)$ 来表示，针对每一个 $y_{t+1}=q_j$ ，都要乘以从 $y_t=q_i$ 到 $y_{t+1}=q_j$ 的状态转移概率 $a_{ij}$ ， $y_{t+1}$ 一共有N种状态，所以：
$\begin{aligned} a_{ij}b_{jx_{t+1}}\beta_{t+1}(j)&=p(x_{t+1},x_{t+2},...,x_T|y_{t+1}=q_j,\boldsymbol{\lambda})a_{ij}\\ &=p(x_{t+1},x_{t+2},...,x_T|y_{t+1}=q_j,\boldsymbol{\lambda})p(y_{t+1}=q_j|y_t=q_i,\boldsymbol{\lambda}))\\ &=p(x_{t+1},x_{t+2},...,x_T,y_{t+1}=q_j,|y_t=q_i,\boldsymbol{\lambda}) \end{aligned}$

$\begin{aligned}\beta_t(i)&=p(x_{t+1},x_{t+2},...,x_T|y_t=q_i,\boldsymbol{\lambda})\\ &=\sum\limits_{y_{t+1}}p(x_{t+1},x_{t+2},...,x_T,y_{t+1}=q_j,|y_t=q_i,\boldsymbol{\lambda})\\ &=\sum\limits_{j=1}^Na_{ij}b_{jx_{t+1}}\beta_{t+1}(j) \end{aligned}$
所以：
$\beta_t(i)=\sum\limits_{j=1}^Na_{ij}b_{jx_{t+1}}\beta_{t+1}(j),\quad i=1,2,3,...,N$
在这里插入图片描述
3. 当 $t=1$ 时， $\beta_1(i)=p(x_2,x_3,x_4,...,x_T|y_1=q_i,\boldsymbol{\lambda})$ ；按照步骤2的思想，针对 $t=1$ 时刻的每一种状态 $y_1=q_i$ ，都需要乘上初始状态概率向量和相应的发射概率矩阵。
$p(\boldsymbol{x}|\boldsymbol{\lambda})=\sum\limits_{i=1}^N\pi_ib_{ix_1}\beta_{1}(i)$

2.4 一些概率与期望值的计算

利用前向概率和后向概率，可以得到关于单个状态和两个状态概率的计算公式。

给定模型 $\boldsymbol{\lambda}$ 和观测 $\boldsymbol{x}$ ，在时刻 $t$ 处于状态 $q_i$ 的概率，记作 $\gamma_t(i)$ ：
$\gamma_t(i)=p(y_t=q_i|\boldsymbol{x},\boldsymbol{\lambda})$

可以用过前向和后向算法来算：

$\begin{aligned} \gamma_t(i)=p(y_t=q_i|\boldsymbol{x},\boldsymbol{\lambda})=\frac{p(y_t=q_i,\boldsymbol{x}|\boldsymbol{\lambda})}{p(\boldsymbol{x}|\boldsymbol{\lambda})} \end{aligned}$

$\alpha_t(i)$ 定义为时刻 $t$ 部分观测序列为 $\boldsymbol{x}=(x_1,x_2,x_3,...,x_t)$ 且状态为 $q_i$ 的概率， $\beta_t(i)$ 定义为时刻 $t$ 状态为 $q_i$ 的条件下，从 $t+1到T$ 的部分观测序列为 $x_{t+1},x_{t+2},x_{t+3},...,x_T$ 的概率，则两者相乘表示，观察序列为 $\boldsymbol{x}=(x_1,x_2,x_3,...,x_T)$ 且状态为 $q_i$ 的概率，数学表示为：
$\alpha_t(i)\beta_t(i)=p(y_t=q_i,\boldsymbol{x}|\boldsymbol{\lambda})$

$p(\boldsymbol{x}|\boldsymbol{\lambda})=\sum\limits_{y_t}p(y_t=q_i,\boldsymbol{x}|\boldsymbol{\lambda})=\sum\limits_{j=1}^N\alpha_t(i)\beta_t(i)$

所以：

$\gamma_t(i)=\frac{\alpha_t(i)\beta_t(i)}{p(\boldsymbol{x}|\boldsymbol{\lambda})}=\frac{\alpha_t(i)\beta_t(i)}{\sum\limits_{j=1}^N\alpha_t(i)\beta_t(i)}$
2. 给定HMM模型参数 $\boldsymbol{\lambda}$ 和观测序列 $\boldsymbol{x}$ ，在时刻 $t$ 处于状态 $q_i$ 且在时刻 $t+1$ 处于状态 $q_j$ 的概率，记作 $\xi_t(i,j)$ ：
$\xi_t(i,j)=p(y_t=q_i,y_{t+1}=q_j|\boldsymbol{x},\boldsymbol{\lambda})$

使用前向和后向算法来计算：
$\begin{aligned} \xi_t(i,j)&=p(y_t=q_i,y_{t+1}=q_j|\boldsymbol{x},\boldsymbol{\lambda})\\ &=\frac{p(y_t=q_i,y_{t+1}=q_j,\boldsymbol{x}|\boldsymbol{\lambda})}{p(\boldsymbol{x},\boldsymbol{\lambda)}}\\ &=\frac{p(y_t=q_i,y_{t+1}=q_j,\boldsymbol{x}|\boldsymbol{\lambda})}{\sum\limits_{i=1}^N\sum\limits_{j=1}^Np(y_t=q_i,y_{t+1}=q_j,\boldsymbol{x}|\boldsymbol{\lambda})} \end{aligned}$

而 $p(y_t=q_i,y_{t+1}=q_j,\boldsymbol{x}|\boldsymbol{\lambda})$ 表示在模型参数下，观测序列 $\boldsymbol{x}$ 以及 $t$ 时刻状态为 $q_i$ 且时刻 $t+1$ 处于状态 $q_j$ 的概率， $\alpha_t(i)=p(y_t=q_i,x_1,x_2,x_3,...,x_t|\boldsymbol{\lambda})$ 表示在模型参数下，观测序列 $x_1,x_2,x_3,...,x_t$ 以及 $t$ 时刻状态为 $q_i$ 的概率， $\beta_{t+1}(j)=p(x_{t+2},x_{t+3},...,x_T|y_{t+1}=q_j,\boldsymbol{\lambda})$ 表示在模型参数和 $t+1$ 时刻状态为 $q_j$ 的条件下，观察序列为 $x_{t+2},x_{t+3},...,x_T$ ，两者之间差一个从时刻 $t到t+1$ 的状态转移概率以及时刻 $t+1$ 状态 $q_j$ 产生序列 $x_{t+1}$ 的概率：
$\begin{aligned} p(y_t=q_i,y_{t+1}=q_j,\boldsymbol{x}|\boldsymbol{\lambda})&=p(y_t=q_i,x_1,x_2,...,x_t|\boldsymbol{\lambda})p(y_{t+1}|y_t,\boldsymbol{\lambda})\\&\qquad p(x_{t+1}|y_{t+1},\boldsymbol{\lambda})p(x_{t+2},x_{t+3},...,x_T|y_{t+1}=q_j,\boldsymbol{\lambda})\\ &=\alpha_t(i)a_{ij}b_{jx_{t+1}}\beta_{t+1}(j) \end{aligned}$

所以：
$\xi_t(i,j)=\frac{\alpha_t(i)a_{ij}b_{jx_{t+1}}\beta_{t+1}(j)}{\sum\limits_{i=1}^N\sum\limits_{j=1}^N\alpha_t(i)a_{ij}b_{jx_{t+1}}\beta_{t+1}(j)}$

3.将 $\xi_t(i,j)$ 和 $\gamma_t(i)$ 对各个时刻求和，可以得到一些有用的期望值：

在观测 $\boldsymbol{x}$ 下，状态 $q_i$ 出现的期望值： $\sum\limits_{t=1}^T\gamma_t(i)$
在观测 $\boldsymbol{x}$ 下,由状态 $q_i$ 转移的期望值： $\sum\limits_{t=1}^{T-1}\gamma_t(i)$
在观测 $\boldsymbol{x}$ 下,由状态 $q_i$ 转移到状态 $q_j$ 的期望值： $\sum\limits_{t=1}^{T-1}\xi_t(i,j)$

3 模型训练问题及算法

给定训练集 $(\boldsymbol{x}^{(i)},\boldsymbol{y}^{(i)})$ ，估计模型参数 $\lambda=(\boldsymbol{\pi},A,B)$ ，使得在该模型下观测序列概率 $p(\boldsymbol{x}|\lambda)$ 最大。根据训练数据是否有状态序列数据分为：完全数据和非完全数据，分别使用监督学习和非监督学习实现。

3.1 监督学习——最大似然估计

在监督学习中，我们使用极大似然法来估计HMM模型参数。
假设给定训练数据包含S个长度相同的观测序列 $\{(\boldsymbol{x}^1,\boldsymbol{y}^1),(\boldsymbol{x}^2,\boldsymbol{y}^2),...,(\boldsymbol{x}^S,\boldsymbol{y}^S)\}$ ，使用极大似然法来估计HMM模型参数。

初始状态概率向量的估计：
统计S个样本中，初始状态为 $q_i$ 的频率。
$\hat{\pi}_i=\frac{N_{q_i}}{S}$
其中， $N_{q_i}$ 是初始状态为 $q_i$ 的样本数量，S是样本的数量。

状态转移概率矩阵的估计：
设样本中时刻t处于状态 $q_i$ ，时刻t+1处于状态 $q_j$ 的频数为 $A_{ij}$ ，那么状态转移概率矩阵的估计为：
$\hat{a}_{ij}=\frac{A_{ij}}{\sum\limits_{j=1}^NA_{ij}},\quad j=1,2,3,...,N;\quad i=1,2,3,...,N$

发射概率矩阵的估计：
设样本中状态为 $i$ 并观测值为 $j$ 的频数 $B_{ij}$ ，那么状态为 $i$ 观测为 $j$ 的概率 $b_{ij}$ 的估计为：
$\hat{b}_{ij}=\frac{B_{ij}}{\sum\limits_{j=1}^MB_{ij}},\quad j=1,2,3,...,M;\quad i=1,2,3,...,N$

监督学习的方法就是拿频率来估计概率。

3.2 非监督学习——EM算法

假设给定训练数据只包含S个长度为T的观测序列 $\boldsymbol{x}=\{\boldsymbol{x}^1,\boldsymbol{x}^2,,...,\boldsymbol{x}^S\}$ 而没有对应的状态序列，目标是学习HMM模型的参数 $\boldsymbol{\lambda}=(\boldsymbol{\pi},A,B)$ 。将状态序列看作不可观测的隐数据 $\boldsymbol{Y}$ ，HMM模型事实上是一个含有隐变量的概率模型：
$p(\boldsymbol{X}|\boldsymbol{\lambda})=\sum\limits_\boldsymbol{Y}p(\boldsymbol{X}|\boldsymbol{Y},\boldsymbol{\lambda})p(\boldsymbol{Y}|\boldsymbol{\lambda})$
这个参数可以由EM算法实现。

确定数据的对数似然函数
所有观测数据写成 $\boldsymbol{x}=\{x_1,x_2,x_3,...,x_T\}$ ，所有的隐藏状态数据写成 $\boldsymbol{y}=\{y_1,y_2,,...,y_T\}$ ，则完全数据是 $(\boldsymbol{x},\boldsymbol{y})=(x_1,x_2,x_3,...,x_T,y_1,y_2,,...,y_T)$ ，完全数据的对数似然函数是 $\log{p(\boldsymbol{x},\boldsymbol{y}|\boldsymbol{\lambda})}$ 。
Em算法的E步：求Q函数 $\begin{aligned} Q(\boldsymbol{\lambda},\overline{\boldsymbol{\lambda}})&=E_\boldsymbol{y}[\log{p(\boldsymbol{y},\boldsymbol{y}|\boldsymbol{\lambda})}|\boldsymbol{x},\overline{\boldsymbol{\lambda}}]\\ &=\sum\limits_\boldsymbol{y}\log{p(\boldsymbol{x},\boldsymbol{y}|\boldsymbol{\lambda})}p(\boldsymbol{x},\boldsymbol{y}|\overline{\boldsymbol{\lambda}}) \end{aligned}$

其中 $\overline{\boldsymbol{\lambda}}$ 是HMM模型参数的当前估计值， $\boldsymbol{\lambda}$ 是要极大化的HMM模型参数。
$p(\boldsymbol{x},\boldsymbol{y}|\boldsymbol{\lambda})=\pi_{y_1}b_{y_1x_1}a_{y_1y_2}b_{y_2x_2}\cdot ...\cdot a_{y_{T-1}y_T}b_{y_Tx_T}$
所以:
$Q(\boldsymbol{\lambda},\overline{\boldsymbol{\lambda}})=\sum\limits_\boldsymbol{y}\log{\pi_{y_1}p(\boldsymbol{x},\boldsymbol{y}|\overline{\boldsymbol{\lambda}}})+\sum\limits_\boldsymbol{y}[\sum\limits^{T-1}_{t=1}\log{a_{y_ty_{t+1}}]p(\boldsymbol{x},\boldsymbol{y}|\overline{\boldsymbol{\lambda}}})+\sum\limits_\boldsymbol{y}[\sum\limits_{t=1}^T\log{b_{y_tx_t}]p(\boldsymbol{x},\boldsymbol{y}|\overline{\boldsymbol{\lambda}}})$

EM算法的M步：极大化Q函数求模型的参数
第一项：
$\sum\limits_\boldsymbol{y}\log{\pi_{y_1}p(\boldsymbol{x},\boldsymbol{y}|\overline{\boldsymbol{\lambda}}})=\sum\limits_{i=1}^N\log{\pi_ip(\boldsymbol{x},y_1=q_i|\overline{\boldsymbol{\lambda}})}$
注意到 $\sum\limits^{N}_{i=1}{\pi_i}=1$ ，利用拉格朗日乘子法，写出拉格朗日函数：

$\sum\limits_{i=1}^N\log{\pi_ip(\boldsymbol{x},y_1=q_i|\overline{\boldsymbol{\lambda}})}+\gamma(\sum\limits^{N}_{i=1}-1)$

求偏导并令其等于0：

$\frac{\partial}{\partial \pi_i}[\sum\limits_{i=1}^N\log{\pi_ip(\boldsymbol{x},y_1=q_i|\overline{\boldsymbol{\lambda}})}+\gamma(\sum\limits^{N}_{i=1}-1)]=0$

得到：

$p(\boldsymbol{x},y_1=q_i|\overline{\boldsymbol{\lambda}})+\gamma\pi_i=0$

对i求和：
$\gamma=-p(\boldsymbol{x}|\overline{\boldsymbol{\lambda}})$

所以，得到 $\pi_i$ ：

$\pi_i=\frac{p(\boldsymbol{x},y_1=q_i|\overline{\boldsymbol{\lambda}})}{p(\boldsymbol{x}|\overline{\boldsymbol{\lambda}})}$

第二项：
$\sum\limits_\boldsymbol{y}[\sum\limits^{T-1}_{t=1}\log{a_{y_ty_{t+1}}]p(\boldsymbol{x},\boldsymbol{y}|\overline{\boldsymbol{\lambda}}})=\sum\limits_{i=1}^N\sum\limits_{j=1}^N\sum\limits_{t=1}^{T-1}\log{a_{ij}p(\boldsymbol{x},y_t=q_i,y_{t+1}=q_j|\overline{\boldsymbol{\lambda}})}$

类似第一项，应用 $\sum\limits_{j=1}^N=1$ 的拉格朗日乘子法可以求出：
$a_{ij}=\frac{\sum\limits_{t=1}^{T-1}p(\boldsymbol{x},y_t=q_i,y_{t+1}=q_j|\overline{\boldsymbol{\lambda}})}{\sum\limits_{t=1}^{T-1}p(\boldsymbol{x},y_t=q_i|\overline{\boldsymbol{\lambda}})}$

第三项：
$\sum\limits_\boldsymbol{y}[\sum\limits_{t=1}^T\log{b_{y_tx_t}]p(\boldsymbol{x},\boldsymbol{y}|\overline{\boldsymbol{\lambda}}})=\sum\limits_{j=1}^N\sum\limits_{t=1}^{T}\log{b_{jx_t}p(\boldsymbol{x},y_t=q_j|\overline{\boldsymbol{\lambda}})}$

同样使用拉格朗日乘子法，求得：
$b_{jk}=\frac{\sum\limits_{t=1}^Tp(\boldsymbol{x},y_t=q_j|\overline{\boldsymbol{\lambda}})I(x_t=v_k)}{\sum\limits_{t=1}^Tp(\boldsymbol{x},y_t=q_j|\overline{\boldsymbol{\lambda}})}$

3.3 Baum-Welch算法

将EM算法的参数式子分别用前向和后向概率算出的 $\gamma_t(i),\xi_t(i,j)$ 表示则:
$a_{ij}=\frac{\sum\limits_{t=1}^{T-1}\xi_t(i,j)}{\sum\limits_{t=1}^{T-1}\gamma_t(i)}$

$b_{ij}=\frac{\sum\limits_{t=1,x_t=v_j}^T\gamma_t(i)}{\sum\limits_{t=1}^T\gamma_t(i)}$

$\pi_i=\gamma_1(i)$

4 序列预测问题及算法

序列预测问题就是已知模型参数 $\lambda=(\boldsymbol{\pi},A,B)$ ，给定观测序列 $\boldsymbol{x}$ ，求最有可能的状态序列 $\boldsymbol{y}$ ，即求 $p(\boldsymbol{y}|\boldsymbol{x})$ 的最大值。一般有两种解法：近似解法与维特比解法。

4.1 近似解法

近似算法的思想是，在每个时刻 $t$ 选择该时刻最有可能出现的状态 $y_t^*$ ，从而得到一个状态序列 $\boldsymbol{y}=(y_i^*,y_2^*,...,y_t^*)$ ，将它作为预测的结果。
给定模型 $\boldsymbol{\lambda}$ 和观测 $\boldsymbol{x}$ ，在时刻 $t$ 处于状态 $q_i$ 的概率:
$\gamma_t(i)==\frac{\alpha_t(i)\beta_t(i)}{p(\boldsymbol{x}|\boldsymbol{\lambda})}=\frac{\alpha_t(i)\beta_t(i)}{\sum\limits_{j=1}^N\alpha_t(i)\beta_t(i)}$

在每一个时刻最有可能的状态 $y_t^*$ 是：
$y_t^*=\argmax_{1\leq i\leq N}[\gamma_t(i)],\quad t=1,2,3...,T$
从而得到整个序列。
近似算法的优点是计算简单，其缺点是不能保证预测的状态序列整体是最有可能的状态序列，因为预测的状态序列可能有实际不发生的部分。事实上，上述方法得到的状态序列中有可能存在转移概率为0的相邻状态。尽管如此，近似算法仍然是有用的。

4.2 维特比算法（Viterbi algorithm）

维特比算法实际是用动态规划解HMM模型序列预测问题，用动态规划求解概率最大路径（最优路径），一条路径对应一个状态序列。
根据图论，假设最优路径为 $\boldsymbol{y}^*$ ，其中从起点到时刻 $t$ 的一段最优路径是 $(y_1^*,y_2^*,...,y_t^*)$ ，则这部分路径对于后序最优路径（ $y_t^*,y_{t+1}^*,y_{t+2}^*,...,y_T^*$ ）的选取来说一定也是最优的。可以使用反证法来证明：假设存在另一条局部路径 $(y_1^,,y_2^,,...,y_t^,)$ 要优于 $(y_1^*,y_2^*,...,y_t^*)$ ，那么它与（ $y_t^*,y_{t+1}^*,y_{t+2}^*,...,y_T^*$ ）拼接起来蝴蝶刀另一条更优的全局最优路径，与定义矛盾。
根据HMM模型的第一个假设， $y_{t+1}$ 仅仅只与 $y_t$ 相关，所以网状图可以动态规划地搜索。定义：二维数组 $\delta_t(i)$ 表示在时刻 $t$ 以 $q_j$ 结尾的所有局部路径的最大概率。从第一步推到第T步，每次递推都在上一次的N条局部路径中挑选，所以复杂度为 $O(TN)$ 。为了得到路径，还需要定义一个二维数组 $\psi_t(i)$ ，记录每个状态的前驱。

$\delta_t(i)=\max_{y_1,y_2,...,y_{t-1}}p(y_t=q_i,y_{t-1},...y_1,x_t,x_{t-1},...,x_1|\boldsymbol{\lambda})$

$\psi_t(i)=\arg\max_{1\leq j \leq N}[\delta_{t-1}(j)a_{ji}]$

维特比算法：

初始化，当 $t=1$ 时，最优路径的备选由N个状态组成，它的前驱为空：
$\delta_1(i)=\pi_ib_{ix_1},\quad i=1,2,3,..,N$

$\psi_1(i)=0,\quad i=1,2,3,..,N$

递推，当 $t\geq 2$ 时，每条备选的路径像贪吃蛇一样吃入一个状态，长度增加一个单位，根据状态转移概率和发射概率计算花费。找出新的局部最优路径，更新两个数组。
$\delta_t(i)=\max_{1\leq j \leq N}[\delta_{t-1}(j)a_{ji}]b_{ix_t},\quad i=1,2,3,..,N$

$\psi_t(i)=\arg\max_{1\leq j \leq N}(\delta_t(j)a_{ji}),\quad i=1,2,3,..,N$

终止，找出最终时刻 $(\delta_t(i)$ 数组中最大概率 $p^*$ ，以及相应的结尾状态下表 $y_T^*$
$P^*=\max_{1\leq j \leq N}\delta_T(i)$

$y_T^*=\arg\max_{1\leq j \leq N}\delta_T(i)$

回溯，根据前驱数组 $\psi_t$ 回溯前驱状态，取得最优路径状态下标 $\boldsymbol{y}^*=(y_1^*,y_2^*,...,y_T^*)$ 。
$y_t^*=\psi_{t+1}(y_{t+1}^*),\quad t=T-1,T-2,...,1$

举个例子：
上文中的盒子和球模型，状态集合为 $Q=\{1,2,3\}$ ，观测集合为 $V=\{红，白\}$ ，
$A=\begin{bmatrix} 0.5 & 0.2 & 0.3\\ 0.3 & 0.5 & 0.2\\ 0.2 & 0.3 & 0.5 \end{bmatrix}$ ， $B=\begin{bmatrix} 0.5 & 0.5 \\ 0.4 & 0.6\\ 0.7 & 0.3 \end{bmatrix}$ ， $\pi=(0.2,0.4,0.4)^T$
设 $T=3$ ， $\boldsymbol{x}=(红，白，红)$ ，求最优状态序列，即最优路径 $\boldsymbol{y}^*=(y_1^*,y_2^*,...,y_T^*)$ 。
解：

初始化，在 $t=1$ 时，对每一个状态 $q_i，i=1,2,3$ ，求状态为 $q_i$ 观测为 $x_1$ 为红的概率，记此概率为 $\delta_1(i)$ 。
$\delta_1(i)=\pi_ib_{ix_1}=\pi_ib_{i红}，\quad i=1,2,3$

$\delta_1(1)=0.2\times0.5=0.1,\delta_1(2)=0.4\times0.4=0.16,\delta_1(3)=0.4\times0.7=0.28$

$\psi_1(i)=0,\quad i=1,2,3$
2. 在 $t=2$ 时，对每个状态 $i，i=1,2,3$ :
$\delta_2(i)=\max_{1\leq j \leq 3}[\delta_{1}(j)a_{ji}]b_{i白},\quad i=1,2,3,..,N$

$\begin{aligned} \delta_2(1)&=\max_{1\leq j \leq 3}[\delta_{1}(j)a_{ji}]b_{i白}\\ &=\max_j\{o.1\times0.5,0.16\times0.3,0.28\times0.2\}\times0.5\\ &=0.028 \end{aligned}$

$\psi_2(1)=3$

同理：

$\delta_2(2)=0.0504,\quad\psi_2(3)=3$

$\delta_2(3)=0.042,\quad\psi_2(3)=3$

同样， $t=3$ ：

$\delta_3(1)=0.00756,\quad\psi_3(1)=2$

$\delta_3(2)=0.01008,\quad\psi_3(2)=2$

$\delta_3(3)=0.0417,\quad\psi_3(3)=3$

最优路径概率:
$P^*=\max_{1\leq i\leq 3}\delta_3(i)=0.0147$

$y_3^*=\argmax_{1\leq j \leq 3}\delta_3(i)=3$

回溯：
$t=2,\quad y_2^*=\psi_3(y_3^*)=\psi_3(3)=3$

$t=1,\quad y_1^*=\psi_2(y_2^*)=\psi_2(3)=3$

所以，最优路径为 $\boldsymbol{y}^*=(y_1^*,y_2^*,y_3^*)=(3,3,3)$ 。

5 hmmlearn使用

hmmlearn是一个实现了hmm的python库，安装很简单，使用pip install hmmlearn就行。
hmmlearn实现了三种HMM模型，分成两类：

针对观测状态是连续的：GaussianHMM和GMMHMM（广泛用于语音识别）
针对观测状态是离散的：MultinomialHMM，也就是上文中提到的。

对于MultinomialHMM的模型，使用比较简单，"startprob_"参数对应我们的初始状态概率向量 $\pi$ ， "transmat_"对应我们的状态转移矩阵 $A$ , "emissionprob_"对应我们的发射概率矩阵 $B$ 。

对于连续观测状态的HMM模型，GaussianHMM类假设观测状态符合高斯分布，而GMMHMM类则假设观测状态符合混合高斯分布。一般情况下我们使用GaussianHMM即高斯分布的观测状态即可。以下对于连续观测状态的HMM模型，我们只讨论GaussianHMM类。

在GaussianHMM类中，"startprob_"参数对应我们的隐藏状态初始分布 $\pi$ , "transmat_"对应我们的状态转移矩阵A, 比较特殊的是发射概率的表示方法，此时由于观测状态是连续值，我们无法像MultinomialHMM一样直接给出矩阵B。而是采用给出各个隐藏状态对应的观测状态高斯分布的概率密度函数的参数。

如果观测序列是一维的，则观测状态的概率密度函数是一维的普通高斯分布。如果观测序列是
N维的，则隐藏状态对应的观测状态的概率密度函数是N维高斯分布。高斯分布的概率密度函数参数可以用μ表示高斯分布的期望向量，Σ表示高斯分布的协方差矩阵。在GaussianHMM类中，“means”用来表示各个隐藏状态对应的高斯分布期望向量μ形成的矩阵，而“covars”用来表示各个隐藏状态对应的高斯分布协方差矩阵Σ形成的三维张量。

参考：深度剖析HMM

5.1 pythonceshi工具unnitest

测试工具unnitest非常容易使用，首先是建立一个继承自TestCase的测试类，然后通过覆盖setUp()完成相关初始化，最后通过覆盖tearDown()方法清除测试中产生的数据，为以后的TestCase留下一个干净的环境。我们需要在测试类中编写以test_开头的测试函数，unnitest会在测试中自动执行以test_开头的测试函数，unnitest的使用框架：

import unittest  
  
class XXXXX(unittest.TestCase):  
  
    def setUp(self):  
	# 自行编写
	pass
 
 
if __name__ == '__main__':  
    unittest.main()

5.2 离散HMM测试

对离散HMM模型的测试代码：

# 计算平方误差
def s_error(A, B):
    return sqrt(np.sum((A-B)*(A-B)))/np.sum(B)
 
 
class DiscreteHMM_Test(unittest.TestCase):
 
 
    def setUp(self):
        # 建立两个HMM，隐藏状态个数为4，X可能分布为10类
        n_state =4
        n_feature = 10
        X_length = 1000
        n_batch = 100 # 批量数目
        self.n_batch = n_batch
        self.X_length = X_length
        self.test_hmm = hmm.DiscreteHMM(n_state, n_feature)
        self.comp_hmm = ContrastHMM(n_state, n_feature)
        self.X, self.Z = self.comp_hmm.module.sample(self.X_length*10)
        self.test_hmm.train(self.X, self.Z)
 
 
    def test_train_batch(self):
        X = []
        Z = []
        for b in range(self.n_batch):
            b_X, b_Z = self.comp_hmm.module.sample(self.X_length)
            X.append(b_X)
            Z.append(b_Z)
 
 
        batch_hmm = hmm.DiscreteHMM(self.test_hmm.n_state, self.test_hmm.x_num)
        batch_hmm.train_batch(X, Z)
        # 判断概率参数是否接近
        # 初始概率判定没有通过！！！
        self.assertAlmostEqual(s_error(batch_hmm.start_prob, self.comp_hmm.module.startprob_), 0, 1)
        self.assertAlmostEqual(s_error(batch_hmm.transmat_prob, self.comp_hmm.module.transmat_), 0, 1)
        self.assertAlmostEqual(s_error(batch_hmm.emission_prob, self.comp_hmm.module.emissionprob_), 0, 1)
 
 
    def test_train(self):
        # 判断概率参数是否接近
        # 单批量的初始概率一定是不准的
        # self.assertAlmostEqual(s_error(self.test_hmm.start_prob, self.comp_hmm.module.startprob_), 0, 1)
        self.assertAlmostEqual(s_error(self.test_hmm.transmat_prob, self.comp_hmm.module.transmat_), 0, 1)
        self.assertAlmostEqual(s_error(self.test_hmm.emission_prob, self.comp_hmm.module.emissionprob_), 0, 1)
 
 
    def test_X_prob(self):
        X,_ = self.comp_hmm.module.sample(self.X_length)
        prob_test = self.test_hmm.X_prob(X)
        prob_comp = self.comp_hmm.module.score(X)
        self.assertAlmostEqual(s_error(prob_test, prob_comp), 0, 1)
 
 
    def test_predict(self):
        X, _ = self.comp_hmm.module.sample(self.X_length)
        prob_next = self.test_hmm.predict(X,np.random.randint(0,self.test_hmm.x_num-1))
        self.assertEqual(prob_next.shape,(self.test_hmm.n_state,))
 
 
    def test_decode(self):
        X,_ = self.comp_hmm.module.sample(self.X_length)
        test_decode = self.test_hmm.decode(X)
        _, comp_decode = self.comp_hmm.module.decode(X)
        self.assertAlmostEqual(s_error(test_decode, comp_decode), 0, 1)
 
 
if __name__ == '__main__':
    unittest.main()

5.3 HMM测试

利用hmmlearn初始化一个高斯模型

class ContrastHMM():
    def __init__(self, n_state, n_feature):
        self.module = hmmlearn.hmm.GaussianHMM(n_components=n_state,covariance_type="full")
        # 初始概率
        self.module.startprob_ = np.random.random(n_state)
        self.module.startprob_ = self.module.startprob_ / np.sum(self.module.startprob_)
        # 转换概率
        self.module.transmat_ = np.random.random((n_state,n_state))
        self.module.transmat_ = self.module.transmat_ / np.repeat(np.sum(self.module.transmat_, 1),n_state).reshape((n_state,n_state))
        # 高斯发射概率
        self.module.means_ = np.random.random(size=(n_state,n_feature))*10
        self.module.covars_ = .5 * np.tile(np.identity(n_feature), (n_state, 1, 1))

利用hmmlearn初始化一个离散HMM模型:

class ContrastHMM():
    def __init__(self, n_state, n_feature):
        self.module = hmmlearn.hmm.MultinomialHMM(n_components=n_state)
        # 初始概率
        self.module.startprob_ = np.random.random(n_state)
        self.module.startprob_ = self.module.startprob_ / np.sum(self.module.startprob_)
        # print self.module.startprob_
        # 转换概率
        self.module.transmat_ = np.random.random((n_state,n_state))
        self.module.transmat_ = self.module.transmat_ / np.repeat(np.sum(self.module.transmat_, 1),n_state).reshape((n_state,n_state))
        # print self.module.transmat_
        # 发射概率
        self.module.emissionprob_ = np.random.random(size=(n_state,n_feature))
        self.module.emissionprob_ = self.module.emissionprob_ / np.repeat(np.sum(self.module.emissionprob_, 1),n_feature).reshape((n_state,n_feature))
        # print self.module.emissionprob_

代码详情请见我的github，请大家帮忙点个star。
在这里插入图片描述

Elenstone

发布了21 篇原创文章 · 获赞 1 · 访问量 1128

私信关注

一文读懂NLP之隐马尔科夫模型（HMM）详解加python实现