文章目录

概率论基础

概率 (probability)
最大似然估计 (maximum likelihood estimation)
条件概率 (conditional probability)
全概率公式 (full probability)
贝叶斯公式(Bayes’ theorem)
贝叶斯决策理论 (Bayesian decision theory)

最小错误率贝叶斯决策
最小风险贝叶斯决策

二项式分布 (binomial distribution)
期望 (expectation)
方差 (variance)

信息论基础

熵
联合熵(joint entropy)
条件熵
相对熵(relative entropy, 或称 Kullback-Leibler divergence, KL 距离)
交叉熵(cross entropy)
困惑度(perplexity)
互信息(mutual information)
噪声信道模型(noisy channel model)

应用举例

词汇歧义消解

习题

概率论基础

概率 (probability)

概率，亦称“或然率”，它是反映随机事件出现的可能性（likelihood)大小。随机事件是指在相同条件下，可能出现也可能不出现的事件。

最大似然估计 (maximum likelihood estimation)

简而言之，最大似然估计的目的就是：利用已知的样本结果，反推最有可能（最大概率）导致这样结果的参数值。

极大似然估计的定义
由于样本集中的样本都是独立同分布，可以只考虑一类样本集 $D$ ，来估计参数向量 $θ$ 。记已知的样本集为： $D = \{ {x_1},{x_2},...,{x_N}\}$
似然函数（linkehood function）：联合概率密度函数 $p(D|\theta )$ 称为相对于 $\{ {x_1},{x_2},...,{x_N}\}$ 的 $θ$ 的似然函数。
$l(\theta ) = p(D|\theta ) = p({x_1},{x_2},...,{x_N}|\theta ) = \prod\limits_{i = 1}^N {p({x_i}|\theta )}$
如果 $\widehat \theta$ 是参数空间中能使似然函数最大的 $θ$ 值，则应该是“最可能”的参数值，那么就是 $θ$ 的极大似然估计量。它是样本集的函数，记作：
$\widehat \theta = d({x_1},{x_2},...,{x_N}) = d(D)$
$\widehat \theta ({x_1},{x_2},...,{x_N})$ 称为极大似然函数估计值。

极大似然函数的定义
极大似然估计（ML估计）：求使得出现该组样本的概率最大的θ值。
$\widehat \theta = \mathop {\arg \max }\limits_\theta l(\theta ) = \mathop {\arg \max }\limits_\theta \prod\limits_{i = 1}^N {p({x_i}|\theta )}$
实际中，为了防止概率相乘得到极小值，常常定义了对数似然函数： $H(\theta)=lnl(\theta)$
$\widehat \theta = \mathop {\arg \max }\limits_\theta H(\theta ) = \mathop {\arg \max }\limits_\theta \sum\limits_{i = 1}^N {\ln p({x_i}|\theta )}$

求解极大似然函数
总结一下，求解极大似然估计函数的值可分为以下几个步骤：

构造似然函数 $l(θ)$
求解对数似然函数 $H(\theta)=lnl(\theta)$
令对数似然函数求偏导为0： $\frac{{dH(\theta )}}{{d\theta }} = \frac{{dln(\theta )}}{{d\theta }} = 0$
解似然方程求出 $θ$ 的极大似然估计 $\widehat \theta$ 。

当参数只有一个和有多个的时候，求解步骤可以归纳为：

未知参数只有一个（θ为标量）
在似然函数满足连续、可微的正则条件下，极大似然估计量是下面微分方程的解： $\frac{{dl(\theta )}}{{d\theta }} = 0$ ，定价于： $\frac{{dH(\theta )}}{{d\theta }} = \frac{{dln(\theta )}}{{d\theta }} = 0$
未知参数有多个（ $θ$ 为向量）
则 $θ$ 可表示为具有 $S$ 个分量的未知向量： $\theta = {[{\theta _1},{\theta _2},...,{\theta _S}]^T}$
我们定义梯度算子为： ${\nabla _\theta } = {[\frac{\partial }{{\partial {\theta _1}}},\frac{\partial }{{\partial {\theta _2}}},...,\frac{\partial }{{\partial {\theta _S}}}]^T}$
若似然函数满足连续可导的条件，则最大似然估计量就是如下方程的解。
${\nabla _\theta }H(\theta ) = {\nabla _\theta }\ln l(\theta ) = \sum\limits_{i = 1}^N {{\nabla _\theta }\ln p({x_i}|\theta )} = 0$
方程的解只是一个估计值，只有在样本数趋于无限多的时候，它才会接近于真实值。

条件概率 (conditional probability)

条件概率是指事件A在另外一个事件B已经发生条件下的发生概率。条件概率表示为： $P（A|B）$ ，读作“在B的条件下A的概率”。
条件概率公式为：
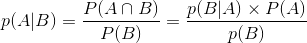
在这里插入图片描述

全概率公式 (full probability)

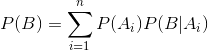
在这里插入图片描述
公式描述：公式表示若事件 $A_1，A_2，…，A_n$ 构成一个完备事件组且都有正概率，则对任意一个事件 $B$ 都有公式成立。

贝叶斯公式(Bayes’ theorem)

与全概率公式解决的问题相反，贝叶斯公式是建立在条件概率的基础上寻找事件发生的原因（即大事件 $A$ 已经发生的条件下，分割中的小事件 $B_i$ 的概率）
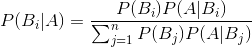
在这里插入图片描述
公式描述：公式中，事件 $B_i$ 的概率为 $P(B_i)$ ，事件 $B_i$ 已发生条件下事件 $A$ 的概率为 $P(A│B_i)$ ，事件 $A$ 发生条件下事件 $B_i$ 的概率为 $P(B_i│A)$ 。

P(B|A) = P(AB) / P(A) , 贝叶斯公式本质上也是条件概率的使用。

贝叶斯决策理论 (Bayesian decision theory)

最小错误率贝叶斯决策

最小错误率分类即最大后验概率决策：对于所有的 $j \ne i$ ，如果满足， $P({\omega _i}|x) > P({\omega _j}|x)$ ，则判给 $\omega _i$ 。

最小风险贝叶斯决策

在这里插入图片描述

二项式分布 (binomial distribution)

二项分布是由伯努利提出的概念，指的是重复n次独立的伯努利试验。在每次试验中只有两种可能的结果，而且两种结果发生与否互相对立，并且相互独立，与其它各次试验结果无关，事件发生与否的概率在每一次独立试验中都保持不变，则这一系列试验总称为n重伯努利实验，当试验次数为1时，二项分布服从0-1分布。
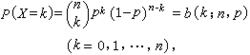
在这里插入图片描述

期望 (expectation)

设 $P(x)$ 是一个离散概率分布函数，自变量的取值范围为 $\{ {x_1},{x_2},...,{x_N}\}$
其期望被定义为：
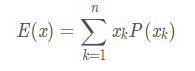
在这里插入图片描述
设 $p(x)$ 是一个连续概率密度函数。其期望为：

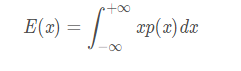
方差 (variance)

反复利用期望的线性性质，可以算出方差的另一种表示形式：
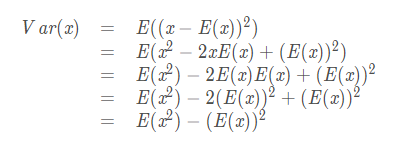
在这里插入图片描述

信息论基础

熵

熵又称为自信息(self-information)，表示信源 X 每发一个符号(不论发什么符号)所提供的平均信息量。熵也可以被视为描述一个随机变量的不确定性的数量。**一个随机变量的熵越大，它的不确定性越大。**那么，正确估计其值的可能性就越小。越不确定的随机变量越需要大的信息量用以确定其值。
在这里插入图片描述

联合熵(joint entropy)

如果 X, Y 是一对离散型随机变量 X, Y ~ p(x, y)， X, Y 的联合熵 H(X, Y) 为：
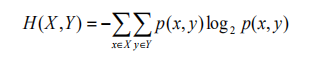
在这里插入图片描述
联合熵实际上就是描述一对随机变量平均所需
要的信息量。

条件熵

给定随机变量 X 的情况下，随机变量 Y 的条件熵定义为：
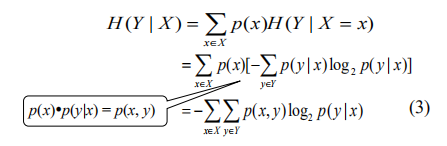
在这里插入图片描述

公式总结：

$\begin{array}{l} H(Y|X) = \sum\limits_{x \in X} {p(x)H(Y|X = x)} \\ \\ = \sum\limits_{x \in X} {p(x)[ - \sum\limits_{y \in Y} {p(y|x){{\log }_2}p(y|x)} ]} \\ \\ = - \sum\limits_{x \in X} {\sum\limits_{y \in Y} {p(x,y){{\log }_2}p(y|x)} } \end{array}$

$H(X, Y ) = H(X) + H(Y|X)$
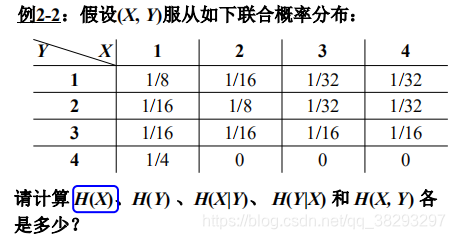
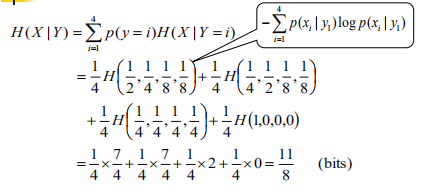
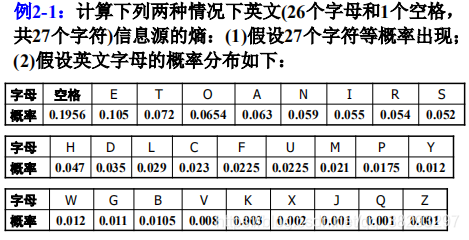
在这里插入图片描述

在这里插入图片描述

下面这个题目，跟上面没有关系

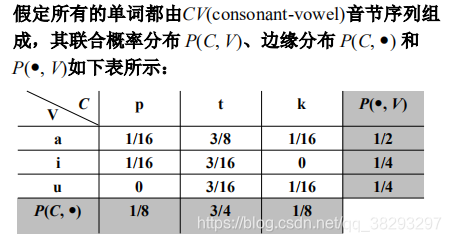
解释：注意,这里的边缘概率是基于每个音节的,其值是基于每个字符的概率的两倍,因此,每个字符的概率值应该为相应边缘概率的1/2。 这里面应该是省略了一个条件： $P(V)=P(C)=1/2$ 。比如求解 $p(a)，则有：p(a)=p(a|V)p(V)=1/4$

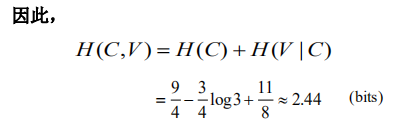
在这里插入图片描述

相对熵(relative entropy, 或称 Kullback-Leibler divergence, KL 距离)

两个概率分布 p(x) 和 q(x) 的相对熵定义为：
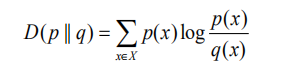
在这里插入图片描述
该定义中约定 $0log (0/q) = 0$ , $plog (p/0) = \infty$ 。
相对熵常被用以衡量两个随机分布的差距。当两个随机分布相同时，其相对熵为0。当两个随机分布的差别增加时，其相对熵也增加。

交叉熵(cross entropy)

如果一个随机变量 X ~ p(x)，q(x)为用于近似 p(x) 的概率分布，那么，随机变量 X 和模型 q 之间的交叉熵定义为：
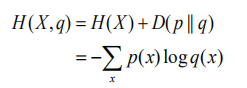
在这里插入图片描述
交叉熵的概念用以衡量估计模型与真实概率分布之间的差异

困惑度(perplexity)

在设计语言模型时，我们通常用困惑度来代替交叉熵衡量语言模型的好坏。给定语言 $L$ 的样本
$l_1^n = {l_1}...{l_n}$ ， $L$ 的困惑度 $PP_q$ 定义为：
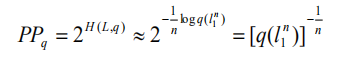
在这里插入图片描述
语言模型设计的任务就是寻找困惑度最小的模型，使其最接近真实的语言。

互信息(mutual information)

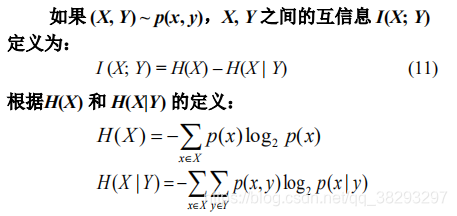
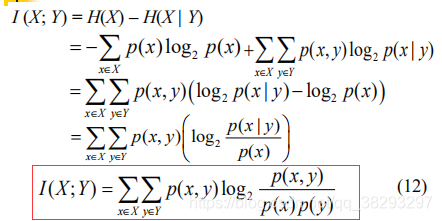
在这里插入图片描述

即 $I(X;Y)=H(X)-H(X|Y)$ ， $H(X)$ 表示 $X$ 的不确定性， $H(X|Y)$ 表示给定Y以后X的不确定性，所以互信息 I (X; Y) 是在知道了 Y 的值以后 X 的不确定性的减少量，即Y 的值透露了多少关于 X 的信息量。

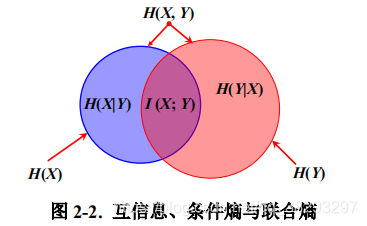
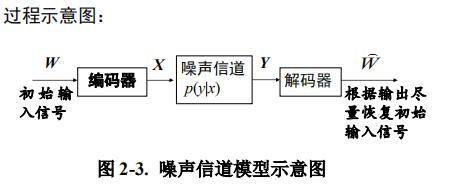
在这里插入图片描述

噪声信道模型(noisy channel model)

在信号传输的过程中都要进行双重性处理：一方面要 通过压缩消除所有的冗余，另一方面又要通过增加一定的 可控冗余以保障输入信号经过噪声信道后可以很好地恢复 原状。信息编码时要尽量占用少量的空间，但又必须保持 足够的冗余以便能够检测和校验错误。接收到的信号需要 被解码使其尽量恢复到原始的输入信号。 噪声信道模型的目标就是优化噪声信道中信号传输的 吞吐量和准确率，其基本假设是一个信道的输出以一定的 概率依赖于输入。

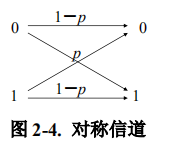
在这里插入图片描述

一个二进制的对称信道(binary symmetric channel, BSC)的输入符号集 $X:{0,1}$ ,输出符号集 $KaTeX parse error: Expected 'EOF', got '}' at position 7: Y:(0,1}̲$ ，在 传输过程中如果输入符号被误传的概率为 $p$ ,那么， 被正确传输的概率就是 $1-p$ 。这个过程我们可以用一 个对称的图型表示如下：
在这里插入图片描述