高数教材班复习Hint

Chapter 1

Lesson 8

${Hint}^1$：设函数 $y=f(x)$在点 $x_0$的某邻域内有定义，如果 $\lim\limits_{\Delta x \to 0}\Delta y=\lim\limits_{\Delta x\to 0}[f(x_0+\Delta x)-f(x_0)]=0$，则称 $f(x)$在点 $x_0$连续。

${Hint}^2$： $\lim\limits_{x\to x_0}f(x)=f(x_0)$说明连续。

${Hint}^3$：

如果函数在去心邻域内有定义，如果 $f(x)$有以下三种情形之一：

$1)$ 在 $x=x_0$处没有定义。
$2)$ 在 $x=x_0$处有定义，但极限不存在。
$3)$ 有定义，有极限，但是 $\lim\limits_{x\to x_0} f(x) \not=f(x_0)$
那么 $f(x)$在 $x_0$处不连续， $x_0$是 $f(x)$的间断点。

${Hint}^4$：

间断点的分类

第一类间断点：左右极限都存在的间断点。
$\left\{ \begin{aligned} 可去间断点：&左右极限存在且相等 \\ 跳跃间断点：&左右极限存在但不相等\\ \end{aligned} \right.$
第二类间断点： 左右极限中至少有一个不存在的间断点。【无穷和振荡】

${Hint}^5$：如果函数在 $x_0$连续，并且 $f(x_0)>0$，则存在 $x_0$的邻域使得当 $x \in U(x_0)$时， $f(x)>0$。【连续函数保号性】

Lesson 9

${Hint}^1$：

连续函数四则运算：
连续函数+不连续函数=不连续函数；
连续函数+连续函数=连续函数
乘除不确定。
复合函数：
仅当连续复合连续才是连续。

${Hint}^2$：反函数和原函数单调性相同。

${Hint}^3$：体会一下特殊函数 $f(x)+g(x)$在取最值上的妙用。

例： 已知 $f(x)$与 $g(x)$在 $x_0$处连续，证明函数 $max\{f(x),g(x)\}，min\{f(x),g(x)\}$在 $x_0$处连续。
证明：
已知 $f(x)$与 $g(x)$在 $x_0$处连续，容易得到 $h(x)=f(x)-g(x)$连续。
令 $p=|h(x)|$，可证 $p(x)$在 $x_0$处连续。
而 $a(x)=max\{f(x),g(x)\}=\frac{f(x)+g(x)+h(x)}{2}$
$b(x)=min\{f(x),g(x)\}=\frac{f(x)+g(x)-h(x)}{2}$

${Hint}^4$：带三角函数的题也要注意和差化积。

例： 求 $\lim\limits_{x\to \alpha}\frac{\sin x-\sin \alpha}{x-\alpha}$
和差化积不需要特地去记，只需要记住：
$\frac{x+y}{2}$和 $\frac{x-y}{2}$代进去即可得到答案。
$PS:$积化和差的时候比较难，需要最好代入所有情况，否则无法直接看出来。
或者背(不提倡）
解：
原式 $=\lim\limits_{x\to \alpha}\frac{2\sin \frac{x-\alpha}{2}\cos \frac{x+ \alpha }{2}}{x-\alpha}=\lim\limits_{x\to \alpha}\frac{2\frac{(x-\alpha)}{2}\cos\frac{x+\alpha}{2}}{x-\alpha}=\lim\limits_{x\to\alpha}\cos{\frac{x+\alpha}{2}}=\cos \alpha$

${Hint}^5$：尽量去凑等价无穷小，凑不成也要凑。

例： $\lim\limits_{x\to e}\frac{\ln x-1}{x-e}$
解：
原式 $=\lim\limits_{x\to e}\frac{\ln\frac{x}{e}}{x-e}=\lim\limits_{x\to e}\frac{\ln(1+\frac{x}{e}-1)}{x-e}=\lim\limits_{x\to e}\frac{\frac{x}{e}-1}{x-e}=\frac{1}{e}$

Lesson 10

${Hint}^1：$对于闭区间则有，有界性与最大值最小值定理。

${Hint}^2：$课堂小知识

$f(x)$关于 $a$对称， $f(x)=f(2a-x) or f(a+x)=f(a-x)$
$f(x)$关于 $a、b$对称, $f(x)=f(x+2b-2a)$

${Hint}^3：$零点存在性定理(前提是连续)

可以推广至开区间的极限， $\lim\limits_{x\to a^+} f(x)*f(b)<0$
奇次幂方程一定有根，因为 $-\infty,+\infty$会使得 $f(a)f(b)<0$

${Hint}^4：$介值定理

设 $f(x)$在闭区间 $[a,b]$上连续，且 $f(a)\not =f(b)$，则对于 $f(a)$和 $f(b)$之间的任何一个数 $\mu$，至少存在一个点 $\epsilon \in(a,b)$，使 $f(\epsilon)=\mu$.
推广，以上最小值到最大值区间都可以取到。

${Hint}^5：$左右只要极限存在，并且保证定义域内连续，就一定有界。

证明也很简单，靠近端点的部分只要有极限，说明邻域有界，然后取两个邻域端点构成闭区间。从而使得整个函数都有界。

${Hint}^5：$和差化积

在实在划不出来的时候，应该把常数项转换成三角函数，进行和差化积。这里其实积形式出来后，上下消去 $\cos$就结束了。
遇到积和差在一块的时候，要把和差化积，这样才能消去某些项。
例： $\lim\limits_{x\to \frac{\pi}{2}}(\sin x)^{\tan x}$
解：

Chapter 2

Lesson 1

${Hint}^1：$ $f'(x_0)$的定义中分子必须包含函数值即 $f(x_0)$。

${Hint}^2：$ $f'(x_0)=A\sim f'(x_0^-)=f'(x_0^+)=A$

${Hint}^3：$可导一定连续，连续不一定可导。

例：
$f(x)=x(x+1)(x+2)...(x+n)$，则 $f'(0)=n!$
用导数定义求解。
遇到一个点的导数要学会用导数定义。
例：
$f'(x_0)$存在， $\lim\limits_{h\to 0}\frac{f(x+h)-f(x-h)}{2h}$不能表示成导数的定义。
$\lim\limits_{h\to 0}\frac{f(x+h)-f(x-h)}{2h}=\frac{1}{2}\lim\limits_{h\to 0}\frac{f(x+h)-f(x)}{h}+\frac{f(x)-f(x-h)}{h}$
能拆开，那么如果这两个极限存在，才能保证该点极限存在，但这两个就是极限定义，即导数。
所以我们不能推导出来其存在。

Lesson 2

${Hint}^1：$可导 $\pm$不可导 $=$不可导

${Hint}^2：$反函数 $x=\phi(y)$导数 $=\frac{1}{f'(x)}$

${Hint}^3：$ $\ln|x|$的导数是 $\frac{1}{x}$

$y=\sqrt{(x-1)(x-2)}$，对数求导法转换成 $\ln y =\ln|x-1|+\ln|x-2|$。
$\frac{y'}{y}=\frac{1}{x-1}+\frac{1}{x-2}$

${Hint}^4$： $f(x)$可导， $f(x_0)=0$， $g(x)$在 $x_0$连续。

若 $g$可导，肯定可导。
若不可导， $\lim\frac{f(x)g(x)-f(x_0)g(x_0)}{x-x_0}=\lim\frac{f(x)g(x)}{x-x_0}=\lim\frac{f(x)g(x)-f(0)g(x)}{x-x_0}=f'(x_0)g(x_0)，即\in$.
若 $f(x)$可导， $g(x)$连续不可导，且只考虑 $x_0$的邻域，则当且仅当 $f(x_0)=0$的时候， $f(x)g(x)$在 $x_0$处可导。

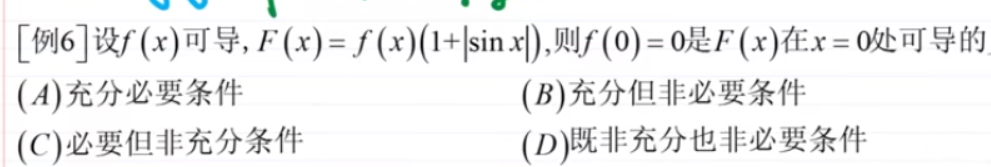
选 $A$。