满足Local Differential Privacy(LDP)的五种编码的介绍

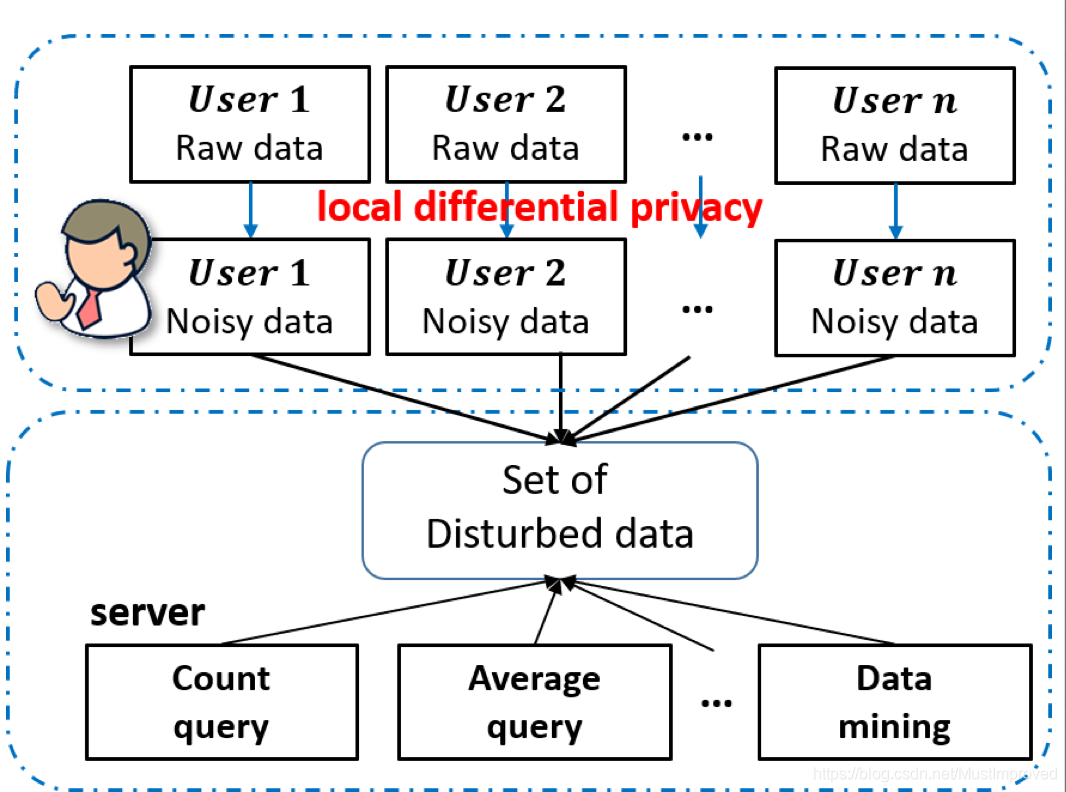
Local Differential Privacy(LDP)可以在收集用户的敏感数据时，保护用户的隐私信息。神奇的LDP，定义是任意两个输入 $v_1,v_2$输出同一个值 $y$的概率的比值在 $e^\varepsilon$界里 ：

如果一个算法 $A$满足 $\varepsilon$-local differential privacy( $\varepsilon$-LDP)，其中 $\varepsilon\geq0$，当且仅当对于任意的输入 $v_1,v_2$，有
$\forall y\in Range(A): Pr[A(v_1)=y]\leq e^{\varepsilon}Pr[A(v_2)=y],$
其中 $Range(A)$表示算法 $A$的所有可能输出的值。

LDP的基本应用是频度估计（即，从n个数据里，统计每个值的出现次数），它可以归结为下面的3个步骤：

1. Encode即编码，由每个用户执行：
   – 输入一个值 $v$；输出一个编码后的值 $x$，即 $x=Encode(v)$；
2. Perturb即扰动，由每个用户执行：
   – 输入一个编码后的值 $x$，输出扰动后的值 $y$，即 $y=Perturb(x)=Perturb(Encode(v))$，后面简记为 $y=PE(v)$；
3. Aggregate即收集，由收集者(Aggregator)执行：
   – 将所有用户扰动后的值 $y$收集，输出处理后的信息，如频度估计。
   
   本文将介绍17-USENIX-Locally Differentially private Protocols for Frequency Estimation¹中所描述的满足LDP的五种编码方法，对它们的比较主要是两个指标：
4. 隐私保护程度 $\varepsilon$，
5. 频度估计（frequency estimation）的方差 $Var(\tilde{c}(i))$。

1. Basic RAPPOR 简化版

规定输入 $v$的值是有限的，为 $d$个。不失一般性，我们 $v$取 $1$到 $d$的整数，即 $v\in[1, d],v\in N$。

1. Encoding: 将输入的整数转化成长度为 $d$ 的01串，对应位取 $1$，其余位取 $0$，即 $Encode(v)=B_0$，其中 $B_0$是长度为 $d$的01串，并保证 $B_0[v]=1,B_0[i]=0, i\neq v$。如 $d=5, v=3$，则 $B_0=00100$;
2. Perturbing: （Rapper是有两次扰动的，此处简化仅考虑一次）01串 $B_0$的每一位分别以 $p$（一般来说， $p\geq \frac{1}{2}$）的概率保持，以 $q=1-p$的概率反转，产生扰动后的01串 $B_1$，即：
   $Pr[B_1[i]=1]=\left\{ \begin{array}{cr} p, &if B_0[i]=1, \\ q=1-p, &if B_0[i]=0. \end{array} \right.$
3. Aggregation: 收集者可以收集到所有用户（设有n个）扰动后的01串 $B_1$，按位估计出原始的个数。记第 $i$位为 $1$的用户个数为 $c(i)$，依此可以估计出扰动前 $B_0$中第 $i$位为 $1$的用户个数 $\tilde{c}(i)$，扰动前的第 $i$ 位为 $1$的有 $p$的概率保持，为 $0$的有 $q=1-p$的概率反转：
   $\begin{aligned} &\ p\cdot\tilde{c}(i)+q\cdot(n-\tilde{c}(i))=c(i) \\ \Rightarrow&\ p\cdot\tilde{c}(i)+(1-p)\cdot(n-\tilde{c}(i))=c(i) \\ \Rightarrow&\ \tilde{c}(i)=\frac{c(i)-(1-p)\cdot n}{2p-1}. \end{aligned}$

$p$是事先约定的， $n$是收集者收集到的用户个数， $c(i)$可以根据收集到的数据累加出来，因此可以比较方便地计算出 $\tilde{c}(i)$。

Privacy: 要达到 $\varepsilon$-LDP，可以取 $\varepsilon=\ln((\frac{p}{1-p})^2)$，证明见2014-Rappor²。

2. Direct Encoding(DE)

依然规定输入 $v$的值是有限的，为 $d$个。

1. Encoding: 正如其名，输入的整数编码成自身，即 $Encode(v)=v$;
2. Perturbing: 依然概率 $p$表示 $v$扰动后得到自身 $v$，概率 $q=\frac{1-p}{d-1}$表示其他值(剩下的 $d-1$个值)扰动后得到 $v$。为了满足LDP的定义，有 $p= e^{\varepsilon}q$，可得到：
   $Pr[Perturb_{DE}(x)=i]=\left\{ \begin{array}{cr} p=\frac{e^{\varepsilon}}{e^{\varepsilon}+d-1}, &if i=x, \\ q=\frac{1}{e^{\varepsilon}+d-1}, &if i\neq x. \end{array} \right.$
3. Aggregation: 收集者可以收集到所有用户（设有n个）扰动后的值 $v'$，按值估计出每个值个数。类似地，记扰动后值为 $i$的用户个数为 $c(i)$，依此可以估计出扰动前值为 $i$的用户个数 $\tilde{c}(i)$，扰动前的值为 $i$的有 $p$的概率保持，非 $i$的有 $q=\frac{1-p}{d-1}$的概率反转：
   $\begin{aligned} &\ p\cdot\tilde{c}(i)+q\cdot(n-\tilde{c}(i))=c(i) \\ \Rightarrow &\ \tilde{c}(i)=\frac{c(i)-q\cdot n}{p-q} \\ \Rightarrow &\ \tilde{c}(i)=\frac{c(i)\cdot(e^{\varepsilon}+d-1)-n}{e^{\varepsilon}-1}, \end{aligned}$
   以及方差¹为
   $Var[\tilde{c}_{DE}(i)]=n\cdot \frac{d-2+e^{\varepsilon}}{(e^{\varepsilon}-1)^2}.$

3. Histogram Encoding(HE)

依然规定输入 $v$的值是有限的，为 $d$个。编码方式和Basic RAPPOR简化版类似，不过由整数变成了实数，扰动的时候加Laplace噪声。

1. Encoding: *将输入的整数转化成长度为 $d$ 的01串，对应位取 $1.0$，其余位取 $0.0$，即 $Encode_{HE}(v)=[0.0, 0.0, ..., 1.0, ..., 0.0]$;
2. Perturbing: $Perturb_{HE}(B)$输出 $B'[i]=B[i]+Lap(\frac{2}{\varepsilon})$;
3. Aggregation: 有两类，分别为SHE, THE，如下：

3.1 Summation with Histogram Encoding(SHE)

Aggregate是求和， $\tilde{c}(i)=\sum_{j}B^{j}[i]$， $j$表示第 $j$个用户。
因为 $Lap(\frac{2}{\epsilon})$是无偏的（均值为 $0$），所以这种方式也是无偏的；
对应的方差¹为
$Var[\tilde{c}_{SHE}(i)]=n\frac{8}{\varepsilon^2}.$

3.2 Thresholding with Histogram Encoding(THE)

Aggregate是设定阈值 $\theta$，大于 $\theta$统计为 $1$，小于等于 $\theta$统计为 $0$。其实也很容易理解，Encoding时在对应数位 $B[v]$取 $1.0$，如果增加的扰动不是太大，一般会大于某个数（取为 $\theta$）；同时 $B[i]$为 $0.0$，如果增加的扰动不是太大，一般会小于某个数（取为 $\theta$）。
此时，可取 $p=1-F(\theta-1),q=1-F(\theta),$
其中 $F(x)$是Laplace分布的累积函数；
一般来说， $\theta\in[0,1]$，此时有
$p=1-\frac{1}{2}e^{\frac{\varepsilon}{2}(\theta-1)},q=1-\frac{1}{2}e^{-\frac{\varepsilon}{2}\theta},$
可得方差¹:
$Var[\tilde{c}_{THE}(i)]=n\frac{2e^{\varepsilon\theta/2}-1}{(1+e^{\varepsilon(\theta-1/2)-2e^{\epsilon\theta/2}})^2}.$

在 $\theta\in(\frac{1}{2},1)$时，THE能取到最优值；因为SHE统计时 $B'[i]$是在整个实数域上的，而THE中统计时 $B'[i]$只有 $0,1$二值，所以 $Var[\tilde{c}_{THE}(i)]<Var[\tilde{c}_{SHE}(i)]$总是成立。

4. Unary Encoding(UE)

和Basic RAPPOR简化版非常相似，Encoding相同，Perturbing（扰动）的时候，概率 $p$表示数位不变，概率 $q$表示数位反转，仍有 $p>q$；这里和Basic RAPPOR简化版不同的地方是 $p+q$可以不为 $1$。
为了保持 $\varepsilon$-LDP，仅需考虑 $v_1,v_2$对应的数位（其他的都相同），最坏情况下， $v1$不变， $v2$反转，可得 $\varepsilon=ln(\frac{p(1-q)}{(1-p)q})$，具体证明可看这里¹。

1. Encoding: 将输入的整数转化成长度为 $d$ 的01串，对应位取 $1$，其余位取 $0$，即 $Encode(v)=[0,...,0,1,0,...,0]$;
2. Perturbing: 01串 $B_0$的每一位分别以 $p$的概率保持，以 $q$( $p+q\neq 1$)的概率反转，产生扰动后的01串 $B_1$，即：
   $Pr[B_1[i]=1]=\left\{ \begin{array}{cr} p, &if B_0[i]=1, \\ q, &if B_0[i]=0. \end{array} \right.$
3. Aggregation: 略。

方差为：
$Var[\tilde{c}_{UE}(i)]=n\cdot\frac{((e^{\varepsilon}-1)q+1)^2}{(e^{\varepsilon}-1)^2(1-q)q}.$

4.1 Symmetric Unary Encoding(SUE)

取 $p+q=1$，此时
$p=\frac{e^{\varepsilon/2}}{e^{\varepsilon/2}+1},q=\frac{1}{e^{\varepsilon/2}+1},$
方差为
$Var[\tilde{c}_{SUE}(i)]=n\cdot\frac{e^{\varepsilon/2}}{(e^{\varepsilon/2}-1)^2}.$

4.2 Optimized Unary Encoding(OUE)

由UE的方差，对 $q$求偏导等于 $0$，可得
$p=\frac{1}{2},q=\frac{1}{e^{\varepsilon/2}+1},$
论文中对 $p,q$取值的含义介绍的很不错， $p$只要对总共只有一个的 $1$扰动，而 $q$要对有 $d-1$个的 $0$进行扰动，因此会对 $0$取较大的隐私预算。
此时的方差为
$Var[\tilde{c}_{OUE}(i)]=n\cdot\frac{4e^{\varepsilon}}{(e^{\varepsilon}-1)^2}.$

5. Local Hashing(LH)

需要先了解一下universal hashing，可以参考我写的博客。其他参考资料有Sarah Adel Bargal的介绍³，用数学的角度来介绍，非常简洁也很清楚；另外wikipedia的universal hashing⁴，用历史的角度来介绍。

universal hashing的基本思想⁵：一个hash函数 $y=h(x)$总是能够针对性地造一组样例，使得hash映射的结果很差很差；一种解决办法（universal hashing）是，我们用一组hash函数（a family of hash functions），每次从中随机选择一个函数作一次映射，平均意义下任意两个不同的输入 $x_1,x_2$的hash函数相同的概率不超过 $\frac{1}{g}$， $g$是hash table的大小。

Binary Local Hashing(BLH)

如果我们选择值域 $g=2$，输出为 $0,1$两种（Binary）。

1. Encoding: 随机均匀地从 $\mathbb{H}$(universal hash function family)选择一个hash函数 $H$，映射输入 $v$，输出hash函数和结果，得 $Encode_{BLH}(v)=<H,b=H(v)>$;
2. Perturbing: 仅对结果 $b$扰动， $Perturb_{BLH}(<H,b>)=<H,b'>$，其中
   $Pr[b']=\left\{ \begin{array}{cr} p=\frac{e^{\varepsilon}}{e^{\varepsilon}+1}, &if\ b=1, \\ q=\frac{1}{e^{\varepsilon}+1}, &if\ b=0. \end{array} \right.$
3. Aggregation: 结合Encoding和Perturbing，可得
   $p*=p,q*=\frac{1}{2},$
   因此，方差为
   $Var[\tilde{c}_{BLH}(i)]=n\cdot\frac{(e^{\varepsilon}+1)^2}{(e^{\varepsilon}-1)^2}.$

Optimized Local Hashing(OLH)

考虑到值域 $g=2$，很容易丢失信息，因此会选择 $g\geq 2$，同时 $g$如果太大的话，也会丢失掉信息。先假设值域为 $g$，则

1. Encoding: 随机均匀地从 $\mathbb{H}$选择一个hash函数 $H$，映射输入 $v$，输出hash函数和结果，得 $Encode_{BLH}(v)=<H,x=H(v)>$;
2. Perturbing: 仅对结果 $b$扰动， $Perturb_{BLH}(<H,x>)=<H,y>$，其中
   $_{\forall i\in[g]}Pr[y=i]=\left\{ \begin{array}{cr} p=\frac{e^{\varepsilon}}{e^{\varepsilon}+g-1}, &if\ x=i, \\ q=\frac{1}{e^{\varepsilon}+g-1}, &if\ x\neq i. \end{array} \right.$
3. Aggregation: 结合Encoding和Perturbing，可得
   $p*=p,q*=\frac{1}{g}p+\frac{g-1}{g}q=\frac{1}{g},$
   因此，方差为
   $Var[\tilde{c}_{LP}(i)]=n\cdot\frac{(e^{\varepsilon}+g-1)^2}{(e^{\varepsilon}-1)^2(g-1)},$
   方差对 $g$求偏导等于 $0$，可得 $g=e^{\varepsilon}+1$，此时 $p*=\frac{e^{\varepsilon}}{e^{\varepsilon}+g-1}=\frac{1}{2},q*=\frac{1}{g}=\frac{1}{e^{\varepsilon}+1}$，所以
   方差为
   $Var[\tilde{c}_{OLH}(i)]=n\cdot\frac{4e^{\varepsilon}}{(e^{\varepsilon}-1)^2}，$
   可以发现OUE和OLH的方差是一样的！非常神奇。

写这篇时，部分参考⁶。第一次写论文相关的，内容比较多、杂，如果大家有什么不懂的，可以随时私信哦。

---

1. https://www.usenix.org/system/files/conference/usenixsecurity17/sec17-wang-tianhao.pdf ↩︎ ↩︎ ↩︎ ↩︎ ↩︎

2. https://arxiv.org/abs/1407.6981 ↩︎

3. https://download.csdn.net/download/MustImproved/12275636 ↩︎

4. universal hashing ↩︎

5. https://blog.csdn.net/MustImproved/article/details/105226276 ↩︎

6. https://zhuanlan.zhihu.com/p/75666425 ↩︎