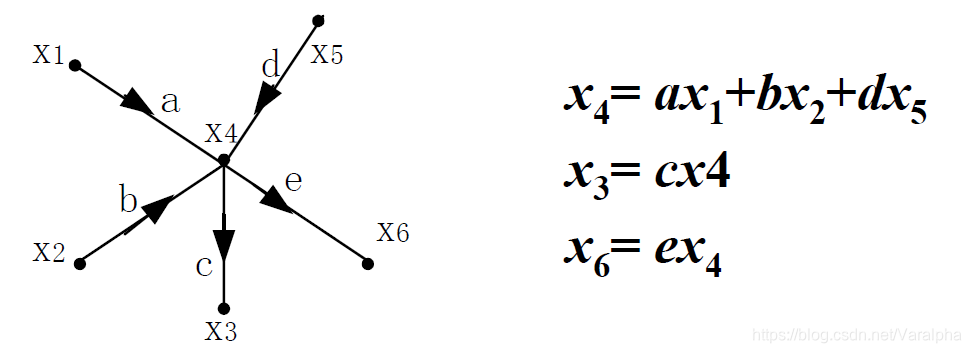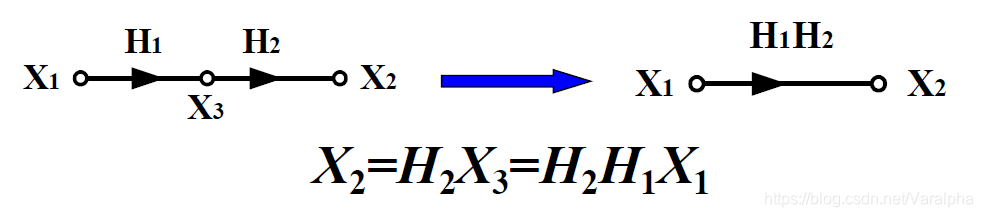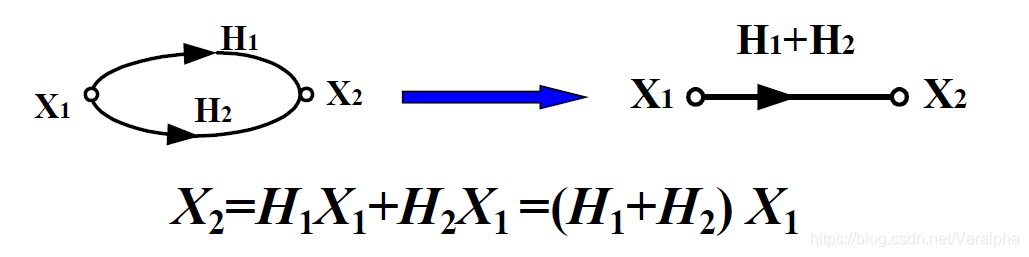文章目录
7.3. 连续系统
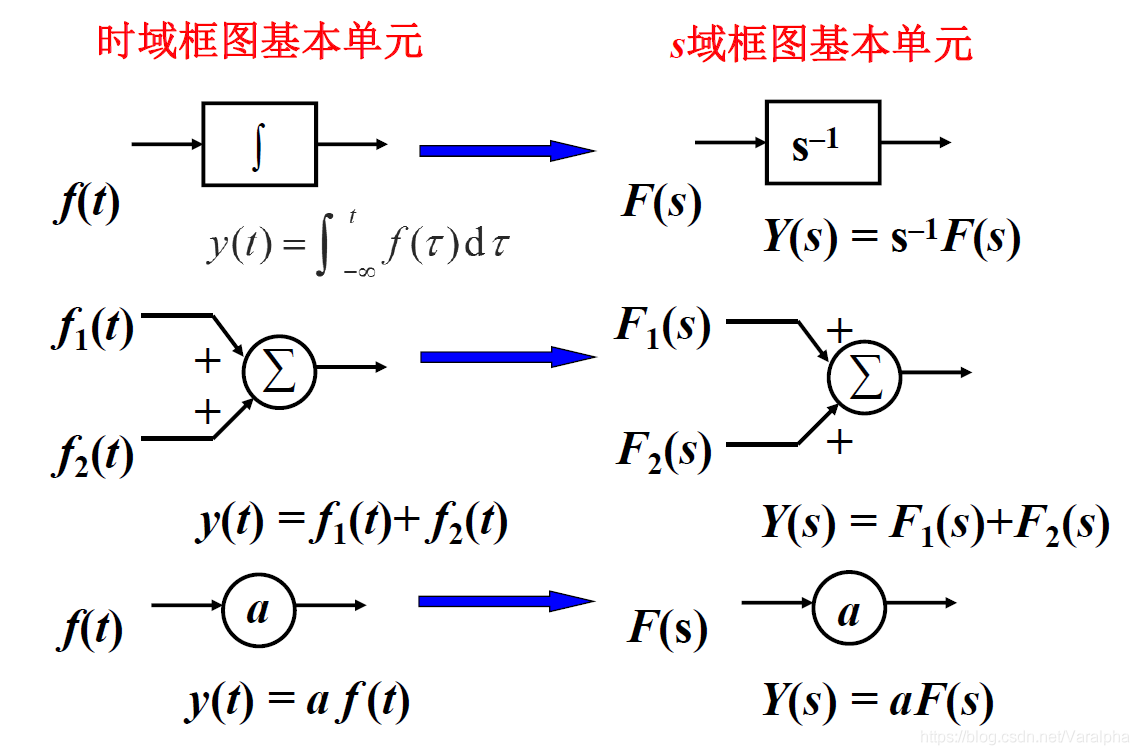
7.3.1. 连续系统的s域框图
-
积分器比微分器在电路中更稳定,所以不用微分器。
- 微分器更容易受到噪声的干扰 – 求导放大噪声
- 积分器累计作用可小的噪声干扰平乏
-
步骤:
- 选择求和器的输出:
- 对求和器的输入 输入 列方程
- 整理
-
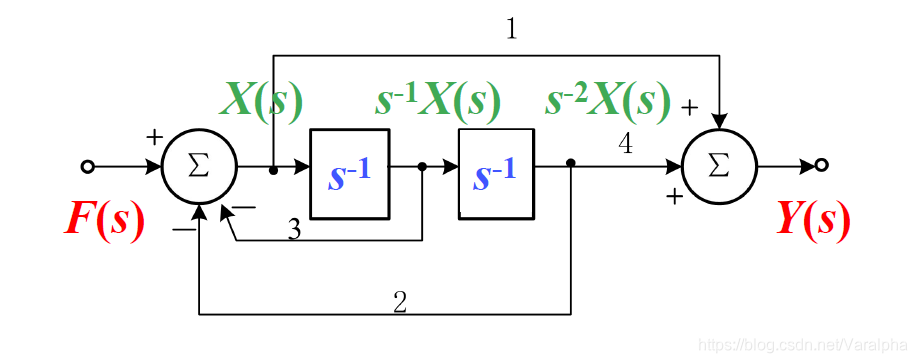
例: 对如下系统列出微分方程:
- 解: 画出 s 域框图,设左边加法器输出为X(s), 如图:
- 为 s 域的代数方程
- 微分方程为
- 为 s 域的代数方程
7.3.2. 连续系统的信号流图
-
系统方框图 简化的表示方法
- 用方框图描述系统的功能比较直观。信号流图由 Mason 1953年提出的,它是用一些点和有向线段描述系统方程变量之间因果关系的一种图,用它描述系统比方框图更加简便,应用非常广泛。
-
定义:信号流图是由结点和有向线段组成的几何图形。它可以简化系统的表示,并便于计算系统函数。
-
信号流图中常用术语
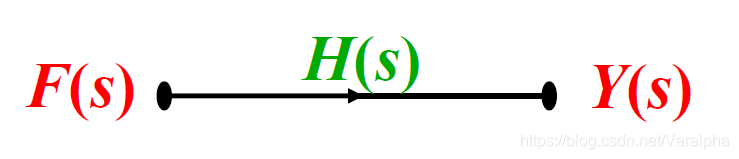
- 结点 :
信号流图中的每个结点表示一个变量或信号。 - 支路和支路增益 :
连接两个结点之间的有向线段称为支路。
每条支路上的权值(支路增益)就是该两结点间的系统函数(转移函数)
即用一条有向线段表示一个子系统。 - 源点与汇点,混合结点 :
仅有出支路的结点称为 源点(或输入结点)。
仅有入支路的结点称为 汇点 (或输出结点)。
有入有出的结点为 混合结点 。 - 通路、开通路、闭通路、不接触回路、自回路 :
通路 -沿箭头指向从一个结点到其他结点的路径。
开通路 -如果通路与任一结点相遇不多于一次。
闭通路 -若通路的终点就是通路的起点(与其余结点相遇不多于一次。
不接触回路 -相互没有公共结点的回路。
自回路 -只有一个结点和一条支路的回路。 - 前向通路,前向通路增益,回路增益 :
前向通路 -从源点到汇点的开通路。
前向通路增益 -前向通路中各支路增益的乘积。
回路增益 -回路中各支路增益的乘积。
- 结点 :
-
信号流图的基本性质
扫描二维码关注公众号,回复: 10252717 查看本文章
- 信号只能沿支路箭头方向传输。
支路的输出 该支路的输入与支路增益的乘积。 - 当结点有多个输入时,该结点将所有输入支路的信号相加,并将和信号传输给所有与该结点相连的输出支路。
- 信号只能沿支路箭头方向传输。
-
方框图 流图
注意:加法器前引入增益为1的支路 -
流图的基本规则
- 支路串联 :支路增益相乘。
- 支路并联 :支路增益相加。
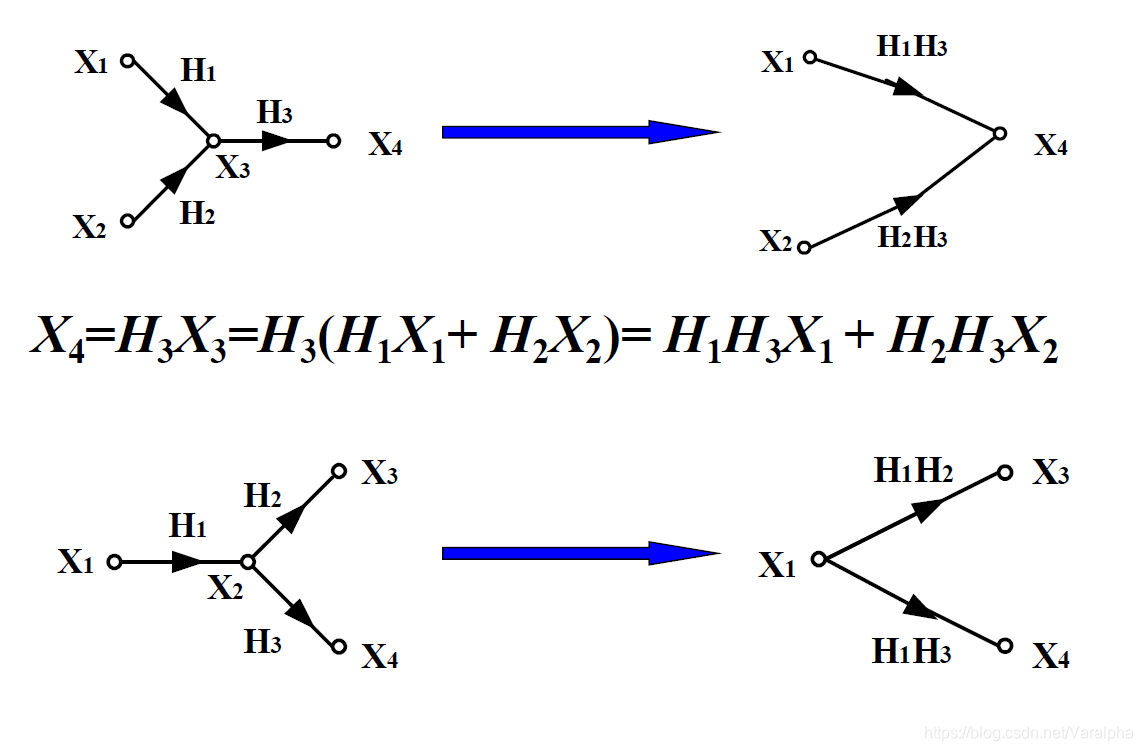
- 混联:
- 支路串联 :支路增益相乘。
7.3.2. 梅森 Mason 公式
-
系统函数 记为 。
-
梅森 Mason 公式为:
- 流图的特征行列式
- 回路(环)
- – 所有不同回路的增益之和
- – 所有两两不接触回路的增益乘积之和
- – 所有三三不接触回路的增益乘积之和
- 表示由源点到汇点的第 条前向通路的标号
- 是由源点到汇点的第 条前向通路增益
- 称为第 条前向通路的剩余特征行列式 (消去接触回路)
- 流图的特征行列式
-
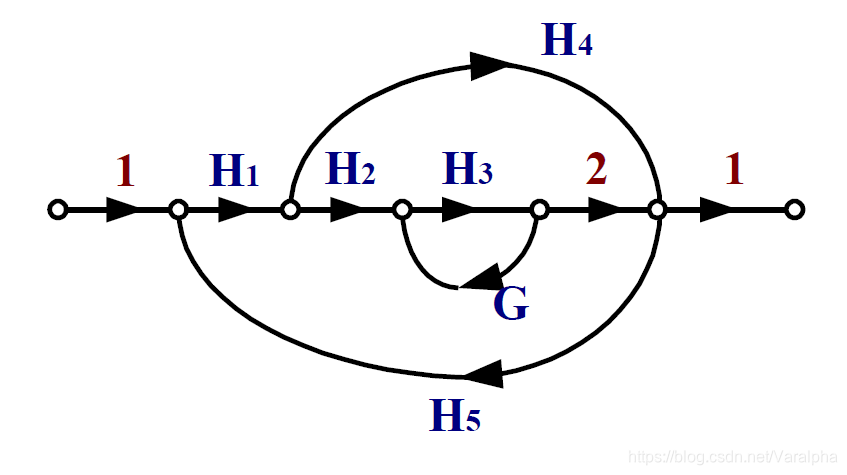
例:求下列信号流图的系统函数
- 首先找出所有回路:
- 两两不相接触
- 求特征行列式:
- 然后找出所有的前向通路
- 求各前向通路的余因子
- 首先找出所有回路:
7.4. 连续系统的模拟
- 若已知 , 给出系统模拟
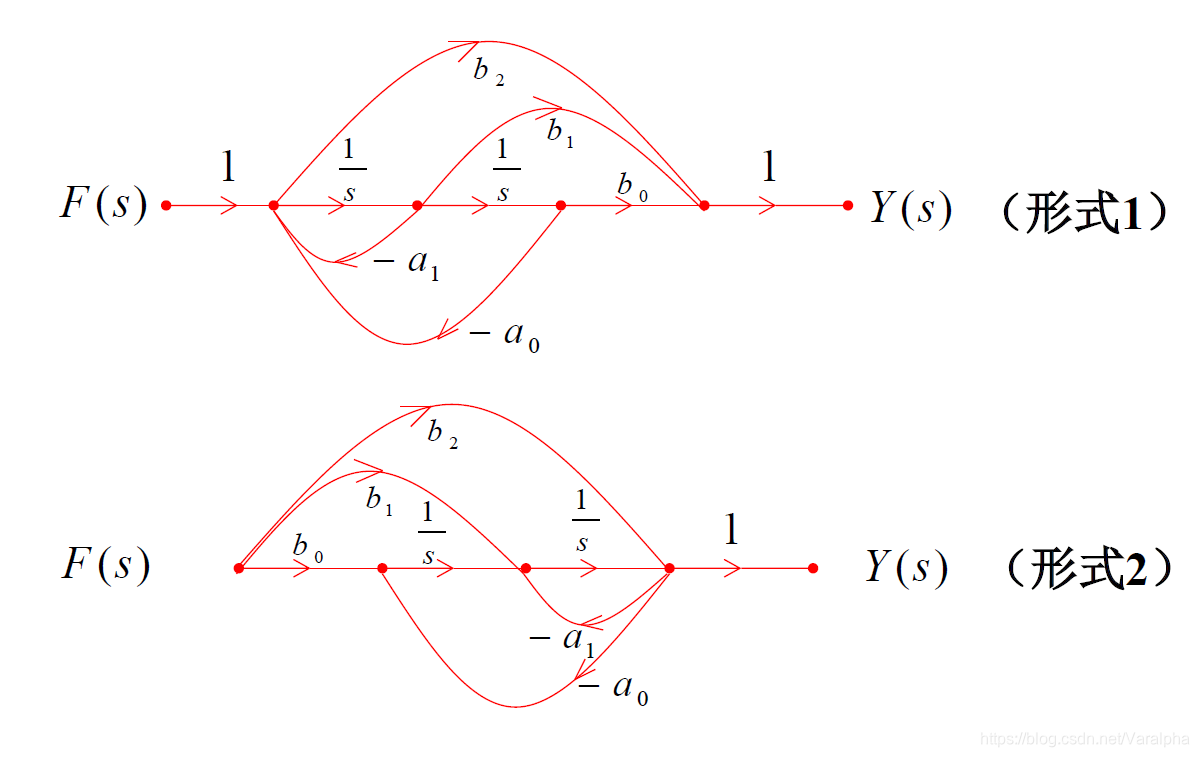
7.3.3. 直接形式
-
利用 Mason 公式来实现
-
思路:
- 构造单环:
- 构造通路: 去掉 ,
-
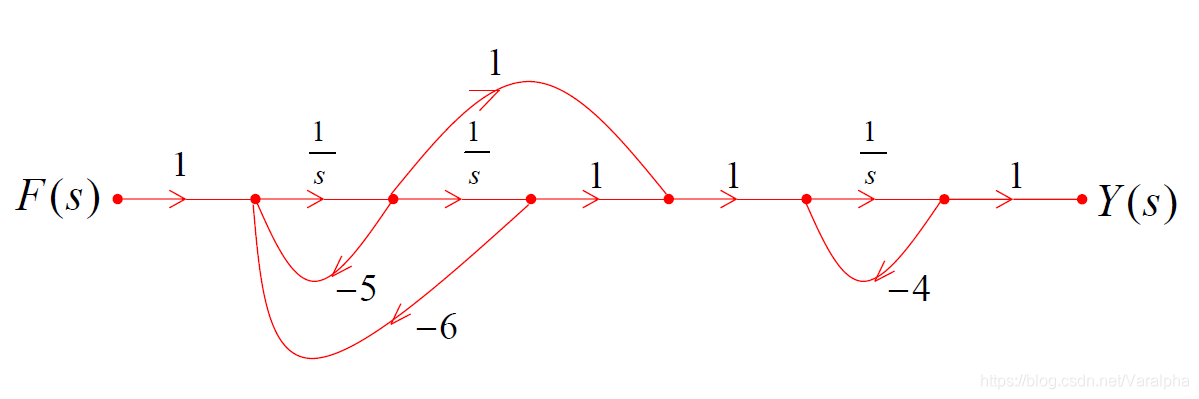
例:
- 画出系统信号流图
-
解:
- 由梅森公式:流图包含3条开路和两个相接触环。
- 两形式都有公用通路点
7.3.4. 级联形式
- 例:
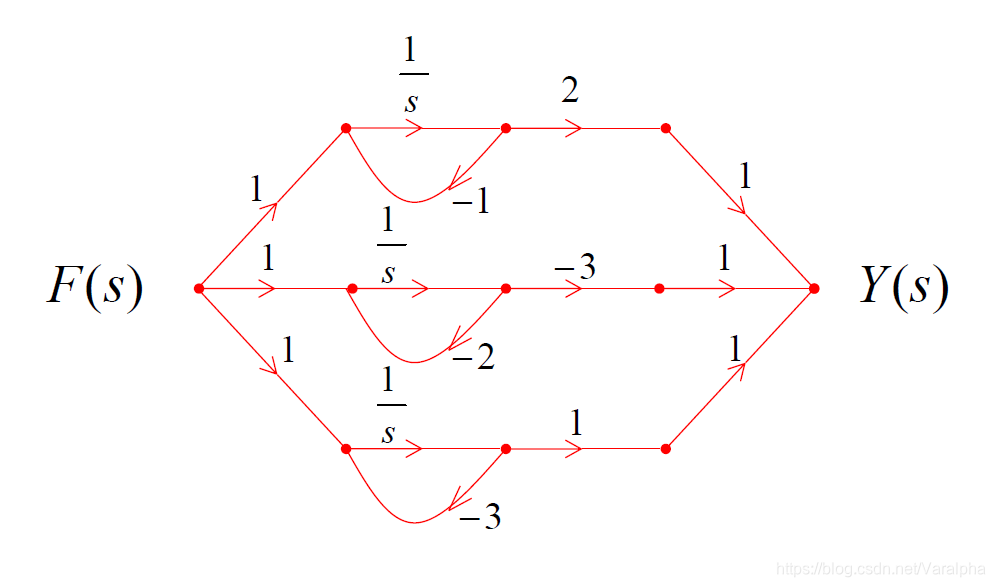
7.3.5. 并联形式
- 例:
7.4. 零极点配置
7.4.1. 零极点配置的作用
-
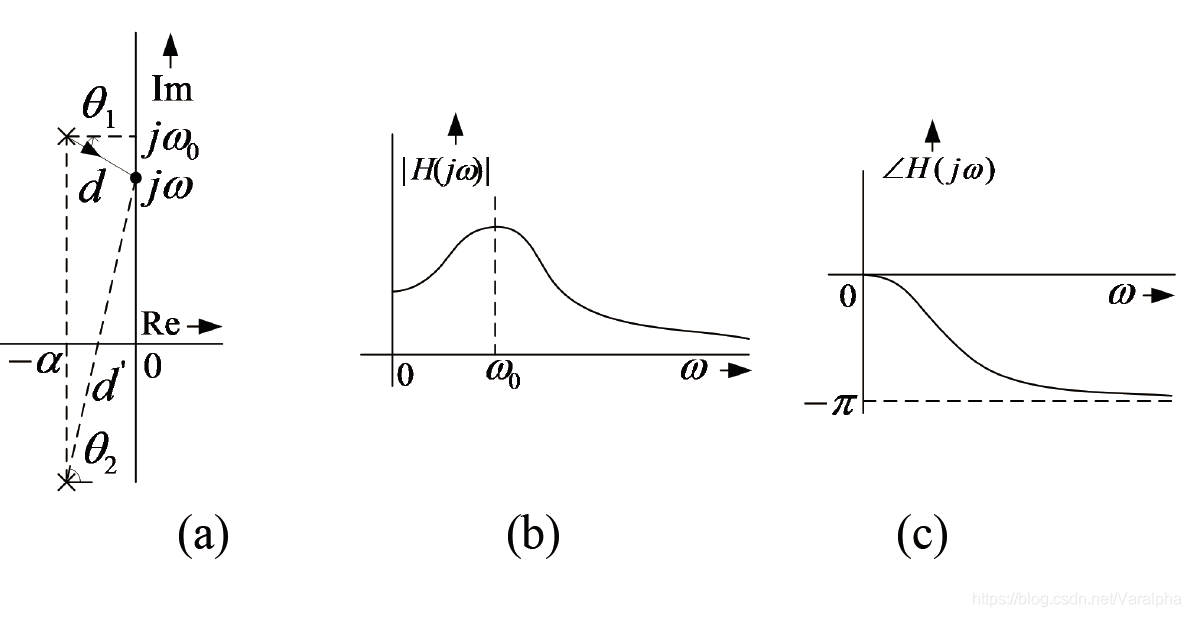
极点增强效益
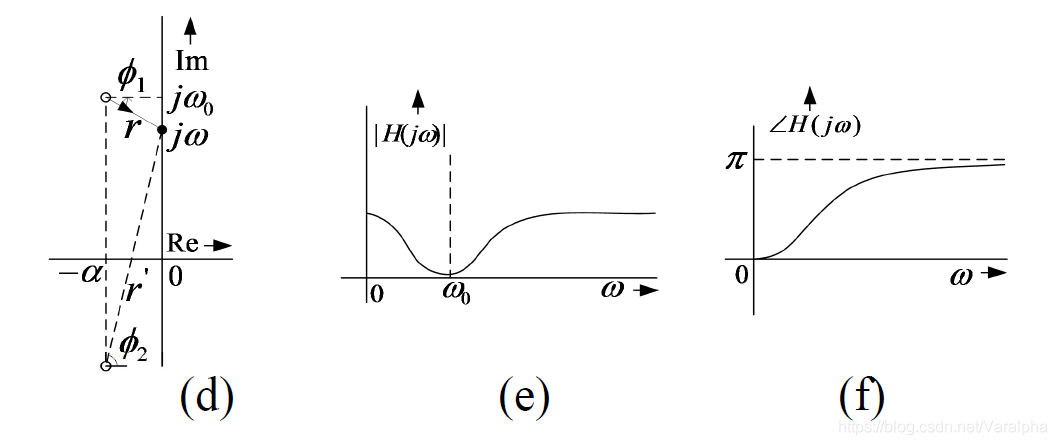
- 假定系统函数只有一个极点
, 如图 (a) 所示。为了对某值
求其幅度
,将该极点
连到虚轴上的
点,假定该线段的长度是
,那么
应正比于
:
- 假定系统函数只有一个极点
, 如图 (a) 所示。为了对某值
求其幅度
,将该极点
连到虚轴上的
点,假定该线段的长度是
,那么
应正比于
:
-
零点抑制效益
- 适当配置零极点对,可以互相抵消在频率响应上的影响,因此,可以利用这些不同的频率选择特性,来观察结果,设计低通、高通、带通和带阻(陷波)滤波器。
7.4.2. 低通滤波器中零极点的配置
-
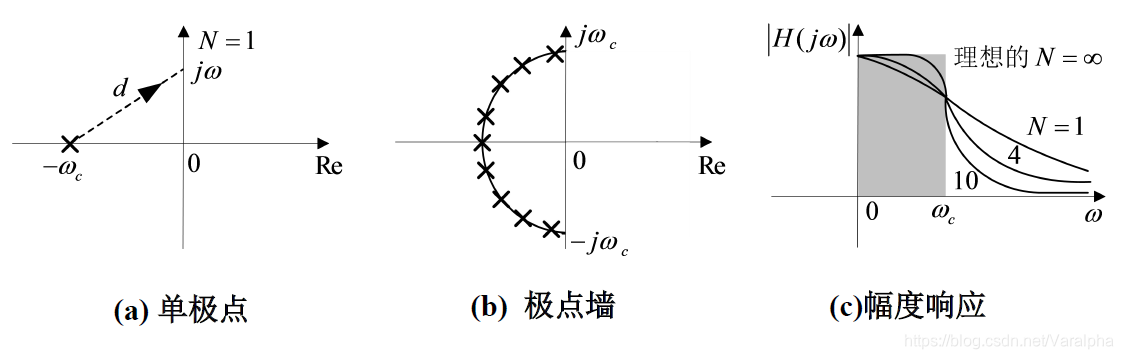
一个典型的低通滤波器在 处 有最大增益。 由于一个极点在它的邻近频率上能使增益增强,所以需要在左半实轴上配置一个(或多个)极点,如图 (a)所示。该系统的系统函数是:
显然
是极点 到虚轴上点 的距离, 且有 。 -
当 增加, 也增大, 单调减少,如图 © 中的 的曲线所示。其在 附近增益被增强。
-
可以证明,为了实现在频带 上所有频率都要增强增益,就需要在左半平面配置无穷多个极点,这些极点位于图 (b) 所示的半圆形墙上,也称 极点墙。
-
对于不同极点个数 的幅度响应如图 ©所示,随着极点个数 ,滤波器接近于理想的。这一类理想滤波器即为 巴特沃茨(Butterworth)滤波器 。
7.4.3. 带通滤波器中零极点的配置
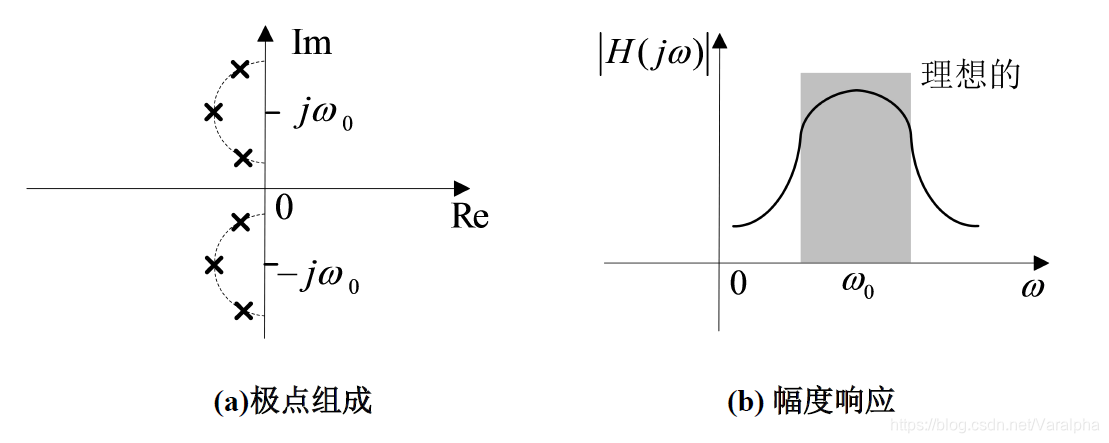
- 阴影特性表示理想带通滤波器的增益,增益在通带内被增强。实现方法为:在左半平面内面对虚轴,以 和 分别为中心配置一堵极点墙,极点墙上所有极点均为共轭极点。理想情况需要无穷多个极点,实际上是用有限个极点去交换一个可以接受的非理想特性。
7.4.4. 带阻滤波器中零极点的配置
-
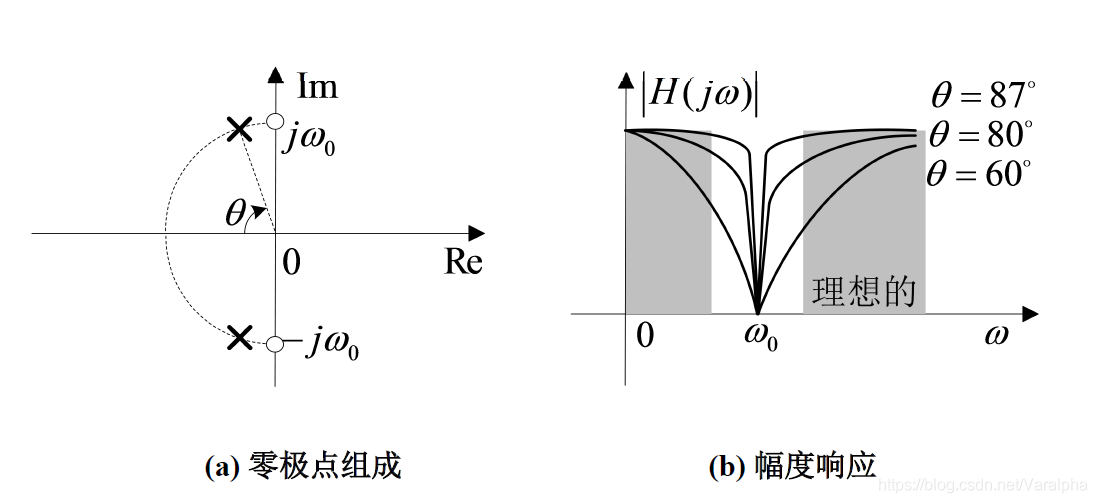
一个理想陷波滤波器的幅度响应(图(b)的阴影部分),与理想带通滤波器的幅度响应刚好相反。以一个二阶陷波滤波器为例,
- 要求在 处得到零增益,为此,必须在 有零点。
- 要求在 增益为 ,就需要极点个数等于零点个数,这就保证了对于 , 极点到 的距离乘积一定等于零点到 的距离乘积。
- 要求 的增益为 ,就需要配置与原点等距离的零点和相应极点,如果采用一对共轭零点,就必须有两个相应极点,并且极点、零点到原点的距离是相同的。此时,只要将两个共轭极点配置在以 为半径的半圆上就能满足这个要求,如图 (a)所示。极点可以位于这个半圆上的任意位置处,均能满足等距离的条件,假定与负实轴成 。
- 由于邻近的极点和零点有相互抵消影响的倾向,故将极点尽可能放置在靠近零点处( 接近 ),这样保证当频率从 向两边稍有变化时,增益能从 到 有一个急剧的恢复,图 (b)是三种不同的 增益。