Lecture 3: Planing by Dynamic programming

Inreoduction

动态规划问题可以把一个复杂的问题分解为多个子问题，然后通过解决这些子问题最终可以解决复杂问题。
动态规划问题的两个特性：

• 最优子结构
• 重复子问题
  MDP满足这两个特性，因此可以用DP解决。
• Bellman方程可以递归分解
• Value function 可以存储并且重复使用解决的子问题

Planning by DP

• Prediction:
  • 输入：MDP $\langle S,A,P,R,\gamma \rangle$ 和Policy $\pi$
  • 输出：value function $v_\pi$
• Control:
  • 输入：MDP $\langle S,A,P,R,\gamma \rangle$
  • 输出：optimal value function $v_*$ 和 optimal policy $\pi_*$

Policy Evaluation

• 问题：评估一个policy $\pi$
• 方法：反向迭代应用bellman 期望方程
• 使用异步反向迭代
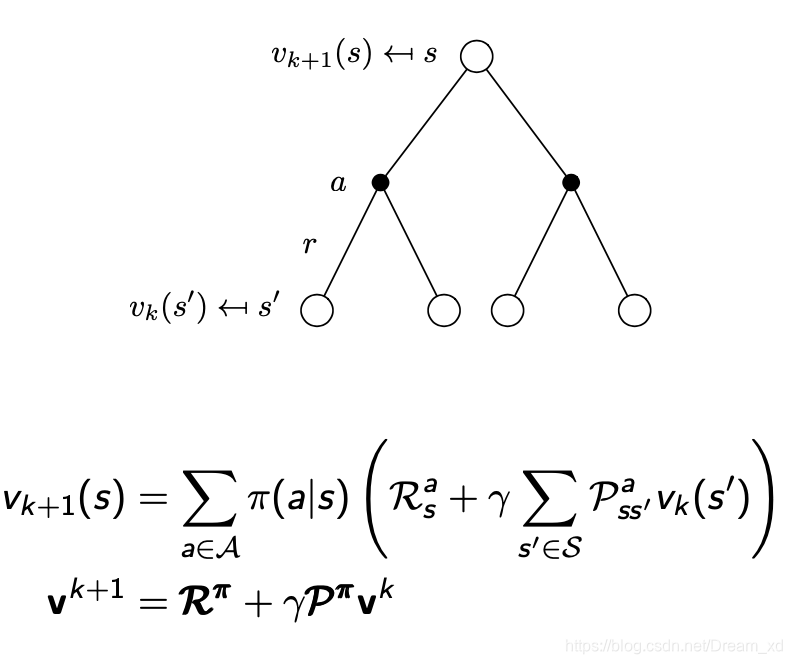
  在每次迭代中，在k+1步时，对于所有的状态 $s \in S$，通过 $v_k(s')$进行更新 $v_{k+1}(s)$，其中，s‘是s的后续状态。
  $v_{k+1}(s) = \sum_{a\in A} \pi(a|s)(R_s^a + \gamma \sum_{s' \in S}P_{ss'}^a v_k(s')$
  矩阵形式：
  $\mathbf{v}^{k+1} =\mathbf{R}^{\pi} + \gamma \mathbf{P}^\pi \mathbf{v}^k$
  

示例-方格世界

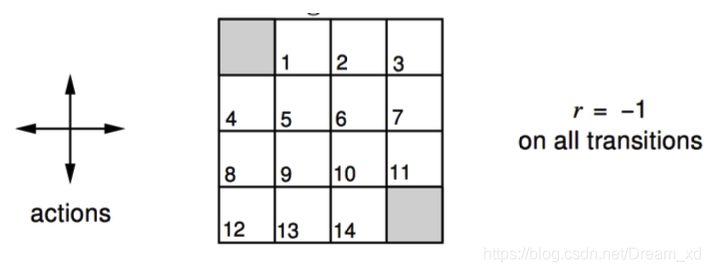
已知：

• 状态空间S：如图。S1 - S14非终止状态，ST终止状态，上图灰色方格所示两个位置；
• 行为空间A：{n, e, s, w} 对于任何非终止状态可以有东南西北移动四个行为；
• 转移概率P：任何试图离开方格世界的动作其位置将不会发生改变，其余条件下将100%地转移到 动作指向的状态；
• 即时奖励R：任何在非终止状态间的转移得到的即时奖励均为-1，进入终止状态即时奖励为0；
• 衰减系数γ：1；
• 当前策略π：Agent采用随机行动策略，在任何一个非终止状态下有均等的几率采取任一移动方向这个行为，即π(n|•) = π(e|•) = π(s|•) = π(w|•) = 1/4。
• 问题：评估在这个方格世界里给定的策略。

迭代法求解（迭代法进行策略评估）

当k=0时，依据当前的value function，无法得出比随机策略更好的策略。
当k=1时，这里解释一下-1（红色标记的）的由来，-1 = 0.25*(-1 + 1.00) + 0.25(-1 + 1.00) + 0.25(-1 + 1.00) + 0.25(-1 + 1.00) ，分别对于上右下左4个行为。0.25为概率，-1为即使奖励，这里都为-1，1.0为衰减因子，0为上一个时刻(也就是k=0)对应状态的value function。
当k=2时，-1.7 = 0.25(-1+1.00)+0.25(-1+1.0*(-1))+0.25*(-1+1.0*(-1))+0.25*(-1+1.0*(-1))
(实际为-1.75，保留以为小数就是-1.7)

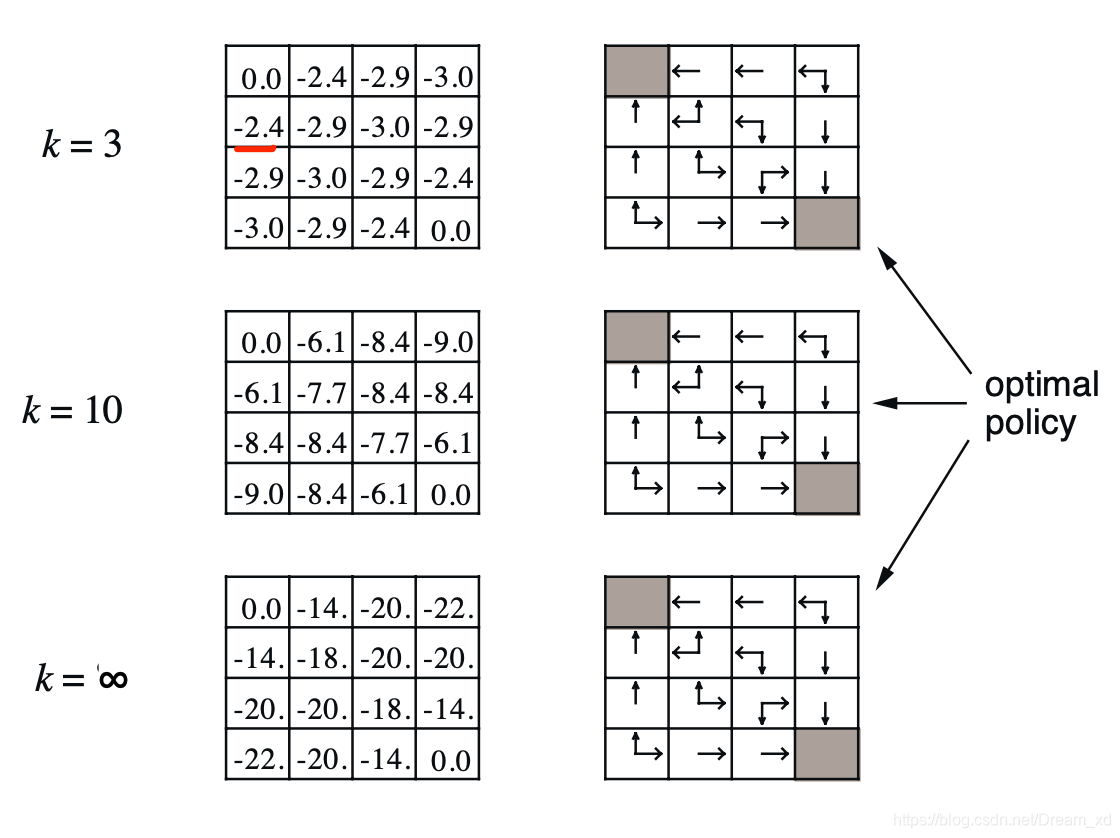
当k=3时，依据该状态价值函数已经可以得到最优策略。-2.4 = 0.25*(-1+ 1.00) + 0.25(-1+ 1.0*(-2.0)) +0.25*(-1+ 1.0*(-2.0)) +0.25*(-1+ 1.0*(-1.7))

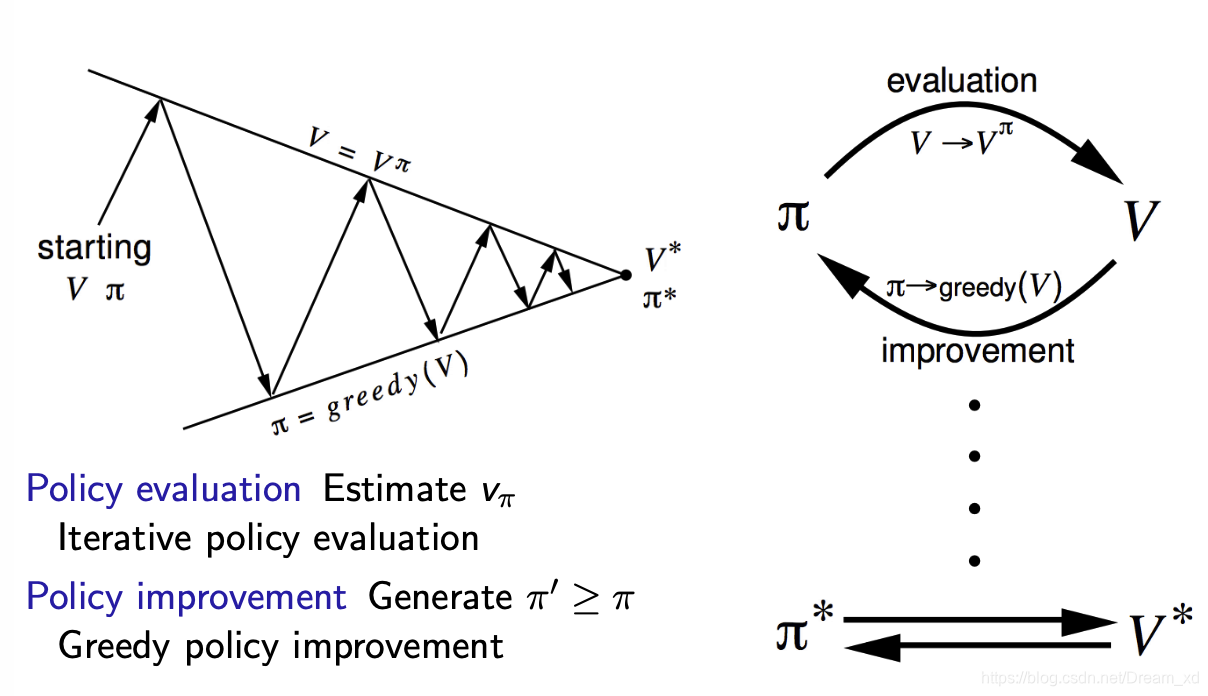
Policy iteration

• 如何提升Policy
  给定一个Policy
  • 评估Policy $\pi$
    $v_\pi(s) = \mathbb{E}[R_{t+1} + \gamma R_{t+2}+ \dots | S_t =s]$
  • 随后，在当前策略基础上，贪婪地选取行为，使得后继状态价值增加最多：
    $\pi' = greedy(v_\pi)$
    在刚才的格子世界中，基于给定策略的价值迭代最终收敛得到的策略就是最优策略，但通过一个回合的迭代计算价值联合策略改善就能找到最优策略不是普遍现象。通常，还需在改善的策略上继续评估，反复多次。不过这种方法总能收敛至最优策略 $\pi^*$ 。
    

示例——连锁汽车租赁

举了一个汽车租赁的例子，说明如何在给定策略下得到基于该策略的价值函数，并根据更新的价值函数来调整策略，直至得到最优策略和最优价值函数。

一个连锁汽车租赁公司有两个地点提供汽车租赁，由于不同的店车辆租赁的市场条件不一样，为了能够实现利润最大化，该公司需要在每天下班后在两个租赁点转移车辆，以便第二天能最大限度的满足两处汽车租赁服务。
已知：

• 状态空间：2个地点，每个地点最多20辆车供租赁
• 行为空间：每天下班后最多转移5辆车从一处到另一处；
• 即时奖励：每租出1辆车奖励10元，必须是有车可租的情况；不考虑在两地转移车辆的支出。
• 转移概率：求租和归还是随机的，但是满足泊松分布 $\frac{\lambda^\pi}{n!}e^{-\lambda}$ 。第一处租赁点平均每天租车请求3次，归还3次；第二处租赁点平均每天租车4次，归还2次。
• 衰减系数 $\gamma$：0.9；
• 问题：怎样的策略是最优策略？
  求解方法：从一个确定的策略出发进行迭代，该策略可以是较为随意的，比如选择这样的策略：不管两地租赁业务市场需求，不移动车辆。以此作为给定策略进行价值迭代，当迭代收敛至一定程度后，改善策略，随后再次迭代，如此反复，直至最终收敛。
  在这个问题中，状态用两个地点的汽车存量来描述，比如分别用c1,c2表示租赁点1,2两处的可租汽车数量，可租汽车数量同时参与决定夜间可转移汽车的最大数量。
  解决该问题的核心就是依据泊松分布确定状态<c1,c2>的即时奖励，进而确定每一个状态的价值。

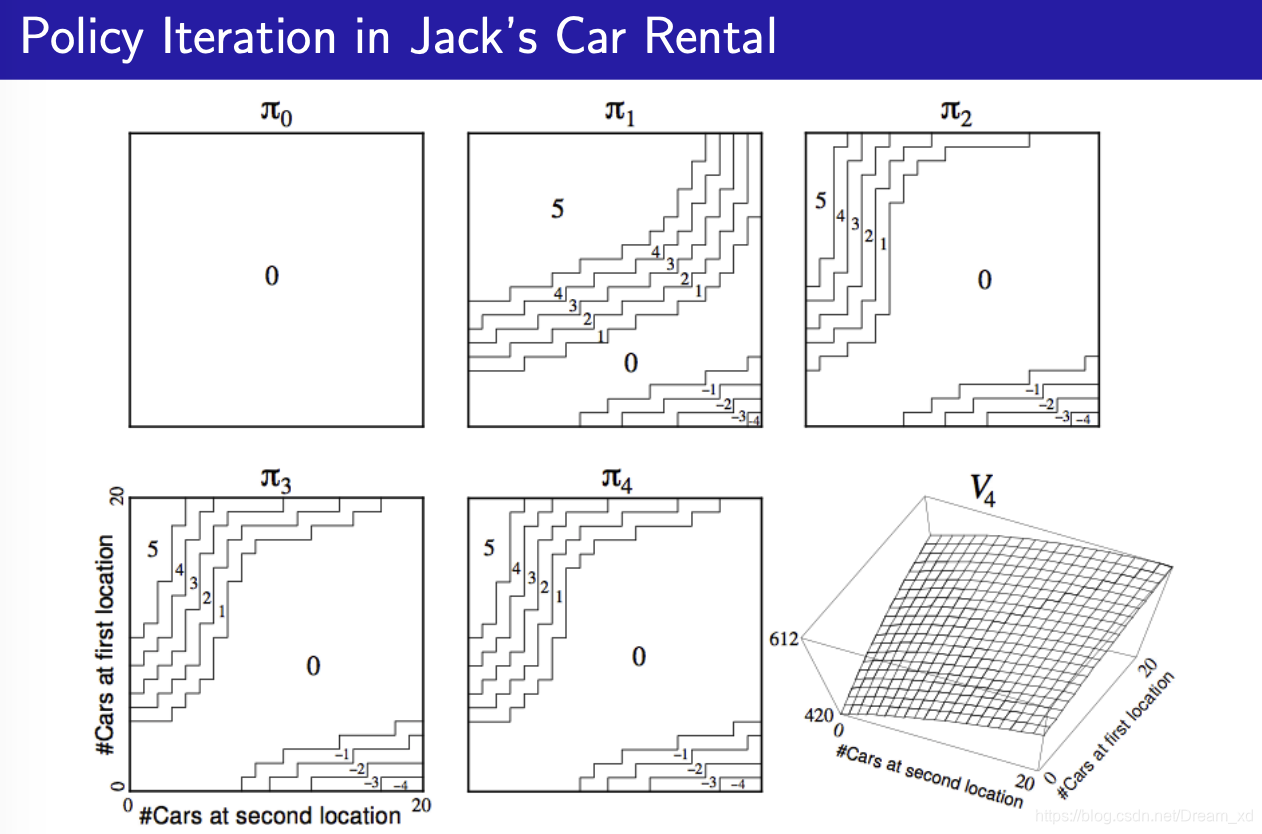
横坐标为第二个位置的汽车数量，纵坐标为第一个位置的汽车数量，图上的数字为需要从第一个位置移动到第二个位置的汽车的数量。

Policy Improvement -理论证明

• 这里考虑确定性policy， $a = \pi(s)$
• 通过贪心提升policy
  $\pi'(s) = \underset{a \in A}{argmax} q_\pi (s,a)$
• 任何状态s经过一次迭代效果都会得到提升
  $q_\pi (s,\pi'(s)) = \underset{a \in A}{argmax} q_\pi (s,a) \ge q_\pi (s,\pi(s)) = v_\pi(s)$
• 因此提升value function， $v_{\pi'}(s) \ge v_\pi(s)$
  
• 如果停止了：
  $q_\pi (s,\pi'(s)) = \underset{a \in A}{argmax} q_\pi (s,a) = q_\pi (s,\pi(s)) = v_\pi(s)$
• 此时，Bellman 最优方程将满足：
  $v_\pi(s) = \underset{a \in A}{argmax} q_\pi (s,a)$
• 因此， $v_\pi(s)=v_*(s)$对于所有的 $s \in S$都成立。
• 此时， $\pi$是最优policy。

改良的策略迭代 Modified Policy Iteration

有时候不需要持续迭代至最有价值函数，可以设置一些条件提前终止迭代，比如设定一个Ɛ，比较两次迭代的价值函数平方差；直接设置迭代次数；以及每迭代一次更新一次策略等。

Value Itertation

Principle of Optimality

一个最优策略可以被分解为两部分：从状态s到下一个状态s’采取了最优行为 $A_*$ ；在状态s’时遵循一个最优策略。

对于确定性价值迭代（Deterministic Value Iteration）

• 如果子问题在状态s‘时候的最优解可以得到 $v_*(s')$
• 那么在状态s时候的最优解就可以一步得到:
  $v_*(s) \leftarrow \underset{a \in A}{max} R_s^a + \gamma \sum_{s' \in S} P_{ss'}^a v_*(s')$

示例——最短路径

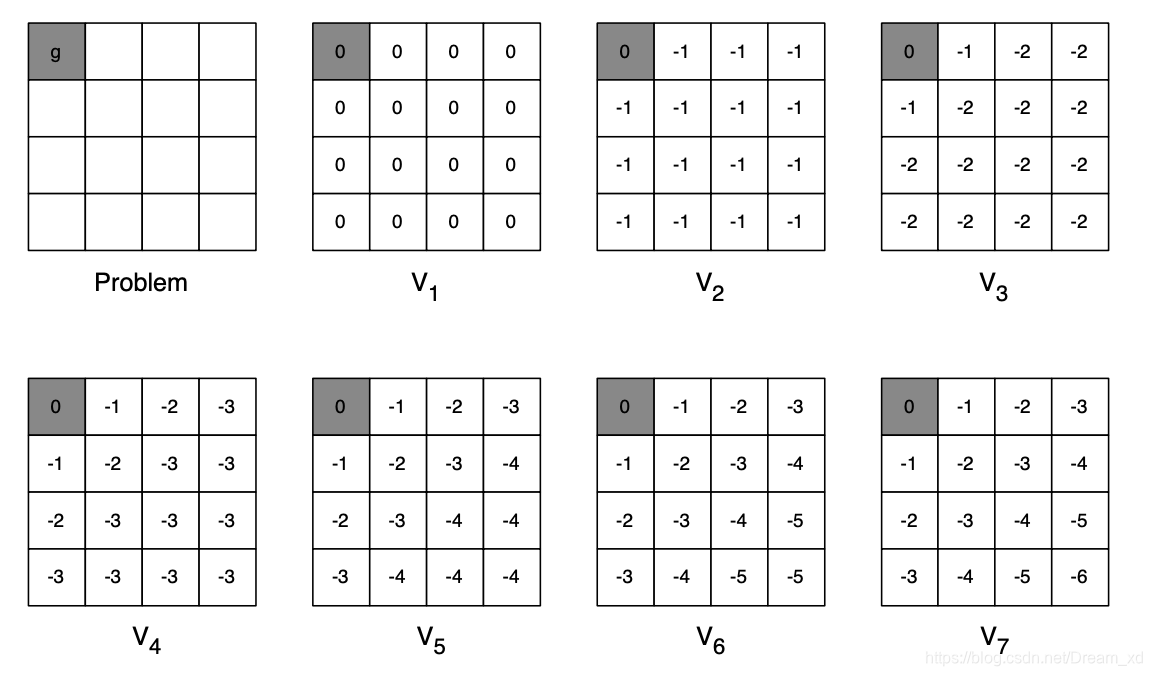
• 问题：如何在一个4*4的方格世界中，找到任一一个方格到最左上角方格的最短路径

• 解决方案1：确定性的价值迭代

  简要思路：在已知左上角为最终目标的情况下，我们可以从与左上角相邻的两个方格开始计算，因为这两个方格是可以仅通过1步就到达目标状态的状态，或者说目标状态是这两个状态的后继状态。最短路径可以量化为：每移动一步获得一个-1的即时奖励。为此我们可以更新与目标方格相邻的这两个方格的状态价值为-1。如此依次向右下角倒推，直至所有状态找到最短路径。

• 解决方案2：价值迭代

  简要思路：并不确定最终状态在哪里，而是根据每一个状态的最优后续状态价值来更新该状态的最佳状态价值，这里强调的是每一个。多次迭代最终收敛。这也是根据一般适用性的价值迭代。在这种情况下，就算不知道目标状态在哪里，这套系统同样可以工作。

Value Iteration

• 问题：寻找最优策略π
• 解决方案：从初始状态价值开始同步迭代计算，最终收敛，整个过程中没有遵循任何策略。
• 注意：与策略迭代不同，在值迭代过程中，算法不会给出明确的策略，迭代过程其间得到的价值函数，不对应任何策略。
  价值迭代虽然不需要策略参与，但仍然需要知道状态之间的转移概率，也就是需要知道模型。
  

小结-DP

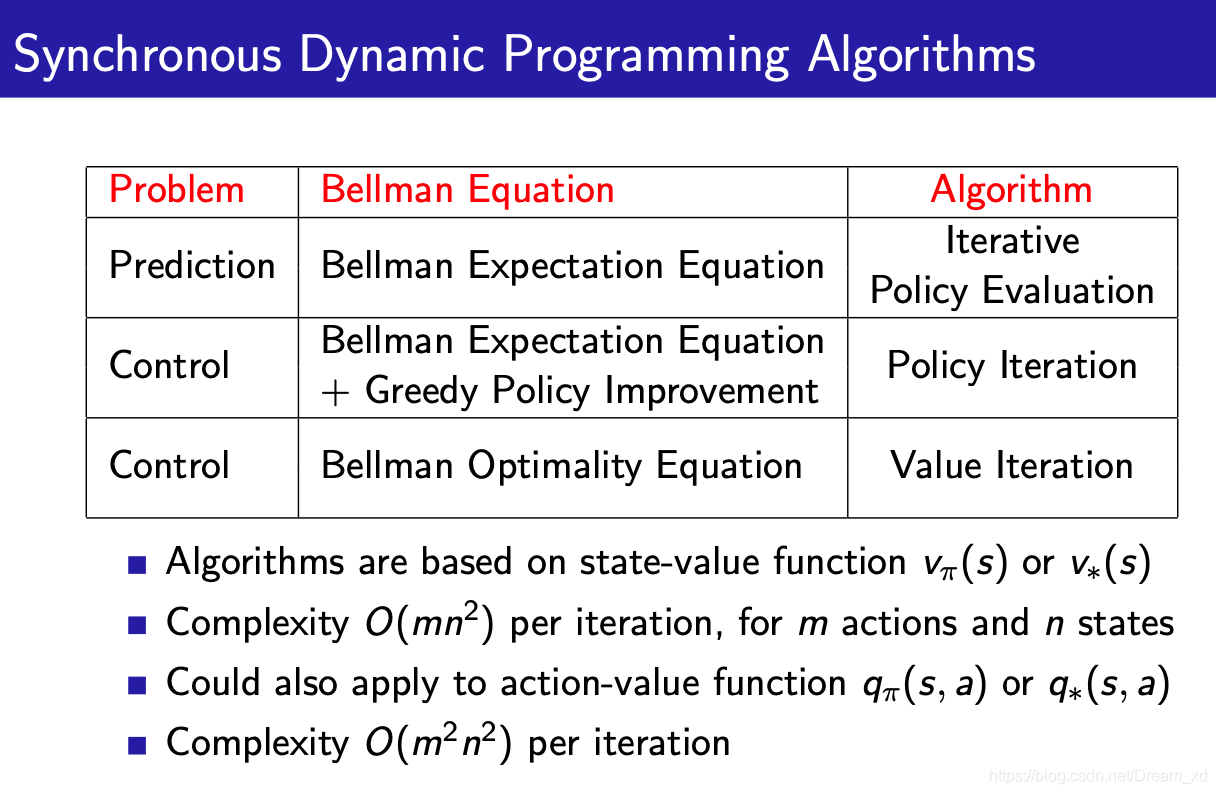
预测问题：在给定策略下迭代计算价值函数。控制问题：策略迭代寻找最优策略问题则先在给定或随机策略下计算状态价值函数，根据状态函数贪婪更新策略，多次反复找到最优策略；单纯使用价值迭代，全程没有策略参与也可以获得最优策略，但需要知道状态转移矩阵，即状态s在行为a后到达的所有后续状态及概率。
使用状态价值函数或行为价值函数两种价值迭代的算法时间复杂度都较大，为 $O(mn^2)$或 $O(m^2n^2)$。一种改进方案是使用异步动态规划，其他的方法即放弃使用动态规划，随后的几讲中将详细讲解其他方法。

Extensions to Dynamic Programming

异步动态规划 Asynchronous Dynamic Programming

In-place Dynamic Programming

直接原地更新下一个状态的v值，而不像同步迭代那样需要额外存储新的v值。在这种情况下，按何种次序更新状态价值有时候会比较有意义。

Prioritised sweeping

对那些重要的状态优先更新。
Bellman error 反映的是当前的状态价值与更新后的状态价值差的绝对值。Bellman error越大，越有必要优先更新。对那些Bellman error较大的状态进行备份。这种算法使用优先级队列能够较得到有效的实现。

Real-time dynamic programming

更新那些仅与agent关系密切的状态，同时使用agent的经验来知道更新状态的选择。有些状态虽然理论上存在，但在现实中几乎不会出现。利用已有现实经验。
St是实际与Agent相关或者说Agent经历的状态，可以省去关于那些仅存在理论上的状态的计算。

采样更新 Sample Backups

动态规划使用full-width backups。意味着使用DP算法，对于每一次状态更新，都要考虑到其所有后继状态及所有可能的行为，同时还要使用MDP中的状态转移矩阵、奖励函数（信息）。DP解决MDP问题的这一特点决定了其对中等规模（百万级别的状态数）的问题较为有效，对于更大规模的问题，会带来Bellman维度灾难。
因此在面对大规模MDP问题是，需要寻找更加实际可操作的算法，主要的思想是Sample Backups，后续会详细介绍。这类算法的优点是不需要完整掌握MDP的条件（例如奖励机制、状态转移矩阵等），通过Sampling（举样）可以打破维度灾难，反向更新状态函数的开销是常数级别的，与状态数无关。

近似动态规划 Approximate Dynamic Programming

使用其他技术手段（例如神经网络）建立一个参数较少，消耗计算资源较少、同时虽然不完全精确但却够用的近似价值函数：

Contraction Mapping

参考

《强化学习》第三讲 动态规划寻找最优策略