Lecture 3：Planning by Dynamic Programming -By David Silver

本文是自己学习David Silver课程的学习笔记：原视频可以在油管或者B站上搜到。

PPT的连接如下：http://www0.cs.ucl.ac.uk/staff/D.Silver/web/Teaching.html。网速慢的话可以点击这里。

Dynamic ：我们认为问题是拥有某种时间或者顺序方面的特性。

Programming：这里我们讨论的是数学规划，就像是线性规划，或者是二次规划。

动态规划能够帮助我们解决一些复杂的问题，就是将复杂的问题分解成子问题，然后去解决这些子问题，将这些子问题的答案结合起来，最终得到原问题的答案。

使用动态规划的方法需要满足两个特性：

1.最优结构：最优化原理，说的是我们可以将某些整体性问题，分解成两个或者多个的子问题，子问题的最优解也就是整体的最优解。简要来说就是整个优化问题可以分解为多个子优化问题。

2.重复的问题：子问题是重复的，这样我们就可以不断重复获得子优化问题的解，使得我们可以将子优化问题的解重复利用。

马尔可夫决策过程是满足动态规划的两个条件的，除此之外，马尔可夫决策过程也满足贝尔曼方程。贝尔曼方程就是递归组合，其中我们将最优值函数拆分两部分，第一步是最优行为，以及在此之后的最优行为。你可以理解为目前的一步行动是最好的，余下的其它步骤也将采取最优的行动，这些就组成了整体的最优值。

我们可以认为Value function就是缓存目前我们所找到MDP的最优值信息。通过value function 我们可以找到从任一状态出发的解决方案。通过value function函数，我们可以找到最优的行动方式。并以那个状态为起点，得到最大奖励。一旦你得到了最优奖励，就可以进行回溯。

这里我们说两个特殊案例的解决方案：

预测问题：

这个问题就是我们知道了一个标准的MDP，我们同时也知道了Policy。我想知道我将会得到多少奖励？针对这个问题，我们需要求解的就是value function，通过value function，我们就可以得到我们能获得的最大奖励是多少。实际上这也是policy评估，通过他我们能知道policy的效果如何。

控制问题：

在这个问题中我们也是知道了MDP的所有信息，像Atari游戏，我们需要知道游戏内部所有的数据，每一步将要产生的数据我们都知道，我们现在想做的就是控制这个游戏，但是我们并不知道policy。我们想知道的是最好的策略是什么？我们想要知道在所有的策略中我们选择哪一个才能得到最多的奖励。也就是找一个最好的状态到动作的映射。

Policy Evaluation

上节课我们是得到了状态值函的计算公式，状态s处的值函是是可以利用后继的值函数V（s'）来表示的。通过高斯-赛德尔迭代算法，我们就可以对其进行求解，求解结果如上图中的公式所示。上面这个方程代表的是值函数的期望形式。

向前看一步，我们向前看的是下一个状态的值。采用贝尔曼方程，每当我们向前看一步，那么我们就得到了下个状态的值，我们所有可能采取的动作都考虑进去，得到接下来的状态，我们考虑这些连续状态的value，在得到下个时刻每一个状态的概率之后，我们将其备份，这样我们就知道了路径上的value值和其对应概率了。

之后的话我们就可以对其进行计算代。我们在叶节点存储我们先前的迭代value。以便我们求得下一次迭代的value，也就是我们想要得到value函数。我们需要最近一次迭代k，将k迭代产生的值带入方程中，得到叶节点的值。通过这些值，我们就能计算出下一次迭代所产生的一个新的value。我们对每个状态都做上述操作，我们就可以将所有状态进行更新求解。

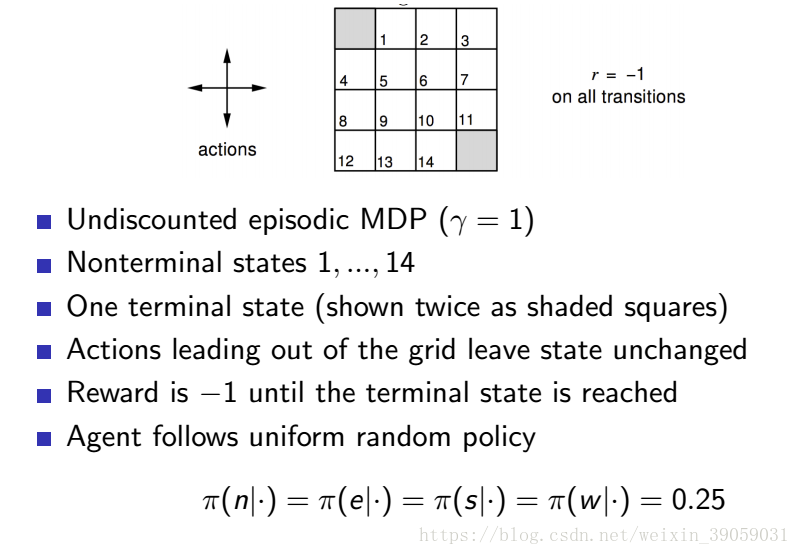
下面举个例子说明一下：

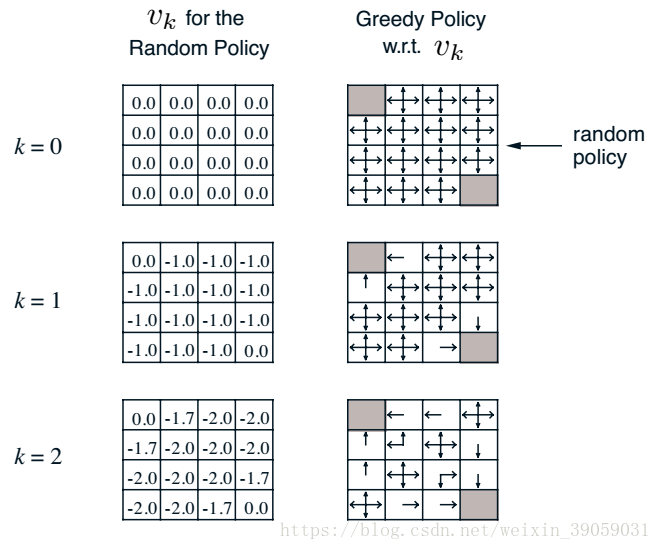
上图是游戏的机制：我们对其迭代求解有：

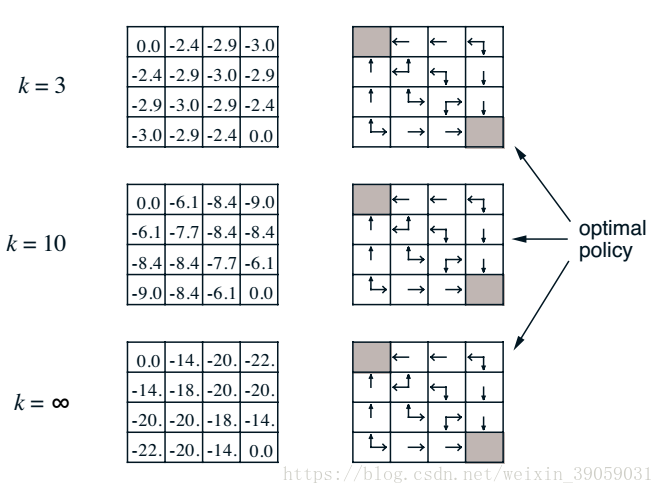
渐渐地，我们发现值函数最终会收敛，也就是当我们策略随机的时候，我们最终到达终点的步长将会是20左右。右侧的表格就是我们在知道value 函数之后构建的新的policy。如果我们忽略右侧的表格，我们可以通过这种策略迭代的方法知道目前我所使用的policy的value。这种方法实际上就是在迭代贝尔曼方程。

Policy Iteration

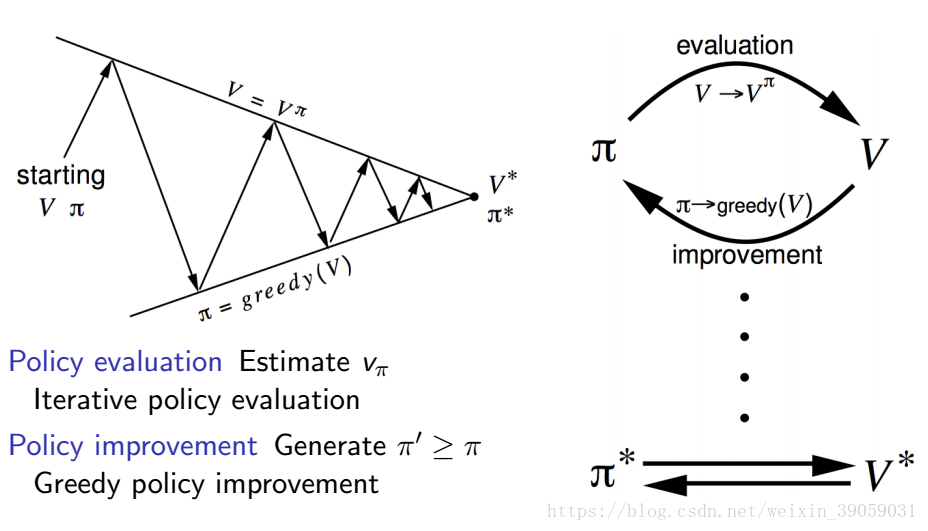
之前我们采取Policy Evaluation的方法能够去评估一个policy。现在我们想要在MDP过程中，寻找一个尽可能好的policy。我们想通过反馈的方式来将其实现。假设某人已近给了你一个policy，你怎么样才能返回一个policy，确保这个policy比原来那个要好。

我们将这个过程分成两部分，第一部分我们将评估这个给定policy的value函数，就像我们在上面policy evaluatioin说的那样，给定一个随机策略，然后更新我们的value函数。第二部分我们依据value函数来改进我们的策略，这里大多数是采用贪心算法（大部分动作的选择采取值函数最大的那一个，小部分采取随机选择）。我们通过第一部分->第二部分->第一部分····这样迭代之后，我们就将会寻找到一个最优的策略。

上面的问题概括起来的话就是下面这张图片：

那么我们现在就推到一下整个策略迭代将会收敛，如下图所示：

我们采用贪婪策略，每次都选取能获得最大价值的那个动作，那么我们得到的奖励至少是和之前的奖励一样大的。通过这样的一次一次迭代之后，我们将会得到一个最优解。

Value Iteration

和策略迭代一样，值函是迭代也是通过回溯的方式来更新整个值函数的。和policy iteration不同的是，我们每一步并不会使用一个已近确定下来的policy，我们只会直接作用于value空间。只有value函数的迭代。

算法的更新过程如下图所示：

其实跟策略迭代没啥多大区别，一个是把动作加进去取max，一个是还没有加动作取max。

证明策略评估的收敛性

在这里我们采用压缩映射（Contraction Mapping）的方法对其实现证明。这个概念在泛函数分析里面有。涉及不动点理论。可以在以下链接中找到一些泛函数分析的教程。

在开始之前我们得先说一下压缩映像：

定义：设 $(X, d)$ $（X, d）$ 是完备的距离空间， $T:X\rightarrow X$ ,如果对于任意的 $x,y\in X$ ,不等式: $d(Tx,Ty)\leq \theta d(x,y)$ 成立，其中 $0<\theta <1$ ,则存在唯一的 $\bar{x}\in X$ 使得 $T\bar{x}=\bar{x}$ 。