递归
递归简单来说就是函数调用自身
例如,下面用迭代和递归的方式分别定义一个计算阶乘的函数
'''迭代方法'''
def factorial(n):
result = n
for i in range(1, n):
result *= i
return result
=================================
'''递归方法'''
def factorial(n):
if n == 0:
return 0
elif n == 1: #递归出口
return 1
else:
return n*factorial(n-1)递归有两个必要因素:
1、有函数调用自身的行为
2、有递归出口(即当符合某条件时停止递归。理论上讲,若忘记设置递归出口,则会无休止的进行下去)
递归会大量消耗时间和空间,所以并不是所有问题都适合用递归来解决(比如上面的求阶乘)。之所以上面说是理论上讲会无休止的进行下去,是因为在某些语言中对递归次数是有默认限制的(比如Python),而有些语言则没有限制(比如C),所以递归次数过多导致的溢出问题则需要程序员自己操心。
'''Python的默认递归次数为100'''
import sys
sys.setrecursionlimit(1000) #可以通过调用sys包中的setrecursionlimit()方法来修改例 汉诺塔问题
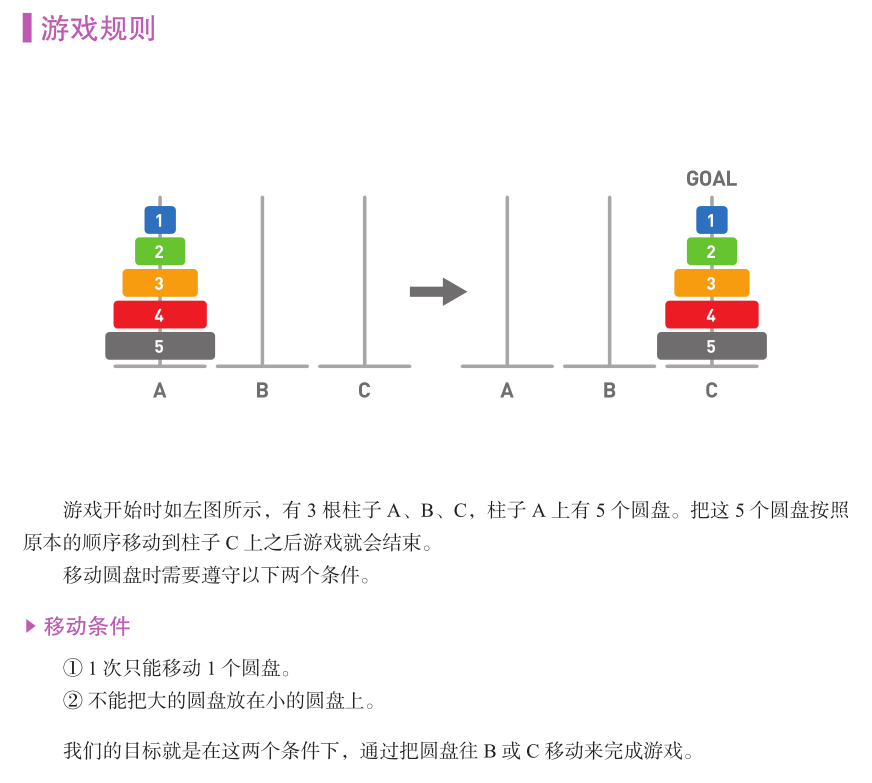
(i) 首先让我们来分析问题,假如只有1个原盘,显然我们可以直接将原盘从A移动到C上
(ii) 而有两个原盘时,则需要将1借助C移动到B上,再将2移动到C上,最后将1借助A移动到C上
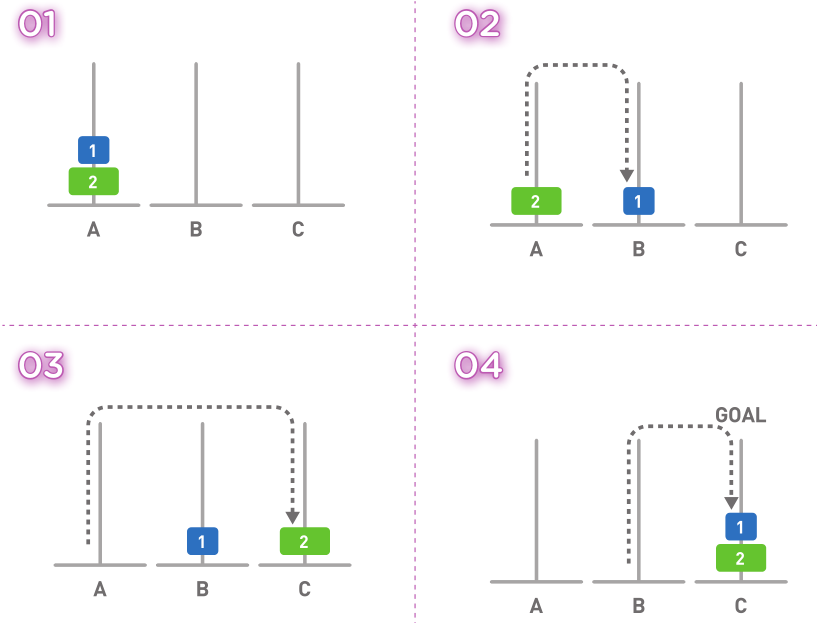
(iii) 当有三个圆盘时,我们要将1、2从A移动到B,将3移动到C,最后将1、2从B移动到C
此时我们可以发现,当圆盘数为n时,问题就可拆解为:
1、将前n-1个圆盘从A借助C移动到B上
2、将第n个圆盘从A移动到C上
3、将前n-1个圆盘从B借助A移动到C上
而其中的1、3步都可以分解为情况(iii)中的三个步骤,第2步即为最简单的情况(i)。
是不是上面的解决方案在文字描述上看起来就已经有了递归的感觉?下面就来试一下代码实现。
cnt = 0 #设置全局变量用来计数
def Hanoi(n, a, b, c): #参数分别为圆盘数,A、B、C柱(从A经过B移动到C)
global cnt #标记cnt为全局变量
if n == 1: #情况(i), 只有一个圆盘时
cnt += 1 #移动一次,移动次数加一
print(a, '--->', c, cnt) #打印圆盘移动路径
else:
Hanoi(n-1, a, c, b) #将前n-1个圆盘从A借助C移动到B上
cnt += 1
print(x, '--->', z, cnt) #将第n个圆盘从A移动到C上
Hanoi(n-1, b, a, c) #将前n-1个圆盘从B借助A移动到C上
Hanoi(5, 'A', 'B', 'C')
输出结果:
a ---> c 1
a ---> b 2
c ---> b 3
a ---> c 4
b ---> a 5
b ---> c 6
a ---> c 7
a ---> b 8
c ---> b 9
c ---> a 10
b ---> a 11
c ---> b 12
a ---> c 13
a ---> b 14
c ---> b 15
a ---> c 16
b ---> a 17
b ---> c 18
a ---> c 19
b ---> a 20
c ---> b 21
c ---> a 22
b ---> a 23
b ---> c 24
a ---> c 25
a ---> b 26
c ---> b 27
a ---> c 28
b ---> a 29
b ---> c 30
a ---> c 31