机器学习（聚类一）——概述

从这篇博客开始，介绍一下无监督学习中最典型的代表——聚类。原本是想讲“分类”这一机器学习最重量级的部分，但内容比较多，所以先讲内容比较少的“聚类”。再介绍具体的聚类算法之前，先简要的说说聚类的概念，以及一些知识点的补充。

什么是聚类

聚类就是对大量未知标注的数据集，按照数据 内部存在的数据特征 将数据集划分为 多个不同的类别 ，使 类别内的数据比较相似，类别之间的数据相似度比较小；属于 无监督学习。

聚类算法的重点是计算样本项之间的 相似度，有时候也称为样本间的 距离。

和分类算法的区别：

• 分类算法是有监督学习，基于有标注的历史数据进行算法模型构建
• 聚类算法是无监督学习，数据集中的数据是没有标注的

有个成语到“物以类聚”，说的就是聚类的概念。直白来讲，就是把认为是一类的物体聚在一起，也就是归为一类（聚在一起的叫一个 簇）。

聚类的思想

给定一个有M个对象的数据集，构建一个具有k个 簇 的模型，其中k<=M（这是肯定的，不可能有3个对象，我划分成4个类吧）。满足以下条件：

• 每个簇至少包含一个对象
• 每个对象属于且仅属于一个簇
• 将满足上述条件的k个簇成为一个合理的聚类划分

总的一个思路就是：对于给定的类别数目k，首先给定初始划分，通过迭代改变样本和簇的隶属关系，使的每次处理后得到的划分方式 比上一次的好 (总的数据集之间的距离和变小了)

相似度/距离公式

上面一直提到什么相似度或距离，特征空间中两个实例点的距离就是两个实例点相似程度的反映。我们也经常用到欧式距离，除此之外还有哪些，这里罗列一些相关公式，因为好多不常用，所以只做简要介绍，或者仅仅提及一下。

1. 闵可夫斯基距离(Minkowski)，也叫范式

对于两个 n 维的数据 $X,Y$
$dist(X,Y)=\sqrt[^{^{^{^p}}}]{\sum_{i=1}^n|x_i - y_i|^p}$
这里 $p \geq1$

也就是先求各维度的差值，然后把这些差值都取 p 次方，接着累加起来，最后把累加的结果开p次方。

（1） 当 $p=1$ 时，称为曼哈顿距离（ Manhattan distance，也称为曼哈顿城市距离），也叫1范式，即
$M\_dist = \sum_{i=1}^n |x_i - y_i|$

以两维的数据为例：

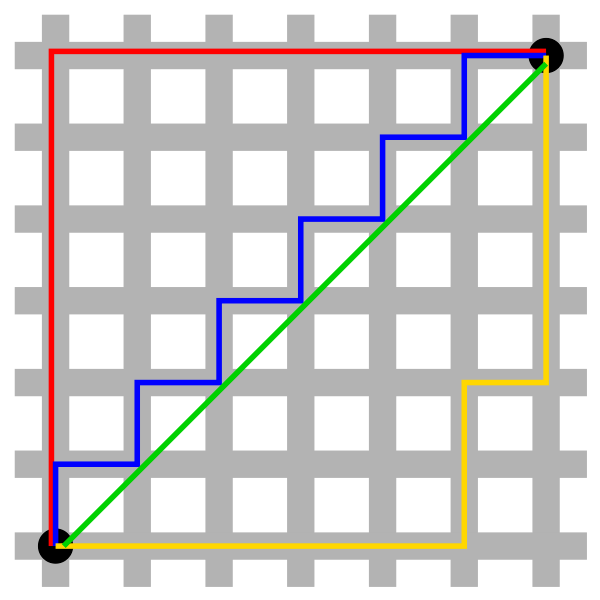
上面的图就像我们的城市公路，比如说从左下角到右上角，我们可以按红线（就是两点间的曼哈顿距离）、蓝线或黄线走，最终都可等效成红线。而绿线就是下面说的欧氏距离。

（2）当 $p=2$ 时，称为欧氏距离 (Euclidean distance) ，也叫2范式，即
$E\_dist=\sqrt{\sum_{i=1}^n|x_i - y_i|^2}$

（3）当 $p=\infty$ 时，称为切比雪夫距离(Chebyshev distance)
$C\_dist=\sqrt[^{^{^{^\infty}}}]{\sum_{i=1}^n|x_i - y_i|^\infty}= \max _i⁡ (|x_i−y_i |)$
也就是上图中，如果横轴的差值大于纵轴的差值，则就为红线中的横线部分；反之就是纵线部分。即，只关心主要的，忽略次要的。

2 . 标准化欧式距离(Standardized Euclidean Distance)

$X^* = \frac{X-\bar{X}}{s}$

这是进行标准化，在数据处理时经常用到。s 表示方差，即 $s=\sqrt{\frac{\sum_{i=1}^n ( s_i - \bar{s})}{n}}$

$标准化的欧式距离 \quad S\_E\_D = \sqrt{\sum_{i=1}^n \left( \frac{x_i -y_i}{s_i} \right)}$

3 . 夹角余弦相似度(Cosine)
$a = (x_{11},x_{12},...,x_{1n}), b = (x_{21},x_{22},...,x_{2n})$
$\cos(\theta) = \frac{\sum_{k=1}^n x_{1k}x_{2k}}{\sqrt{\sum_{k=1}^n x_{1k}^2}*\sqrt{\sum_{k=1}^n x_{1k}^2}} = \frac{a^T \cdot b}{|a||b|}$
其实就是利用了我们中学所学的余弦定理。

4 . KL距离(相对熵)
$D(P||Q)=\sum_x P(x) \log \left( \frac{P(x)}{Q{x}} \right)$
KL距离在信息检索领域，以及自然语言方面有重要的运用。具体内容可以参考《【ML算法】KL距离》

5 . 杰卡德相似系数(Jaccard)
$J(A,B)=\frac{|A \cap B|}{A \cup B}$
目标检测中，经常遇到的IOU，就是这种形式。
$dist(A,B)=1-J(A,B)=\frac{|A \cup B|-|A \cap B|}{|A \cup B|}$
很显然，杰卡德距离是用两个集合中不同元素占所有元素的比例来衡量两个集合的区分度。

6 . Pearson相关系数
$\rho _{XY} = \frac{Cov(X,Y)}{\sqrt{D(X)} \sqrt{D(Y)}} = \frac{E[(X-E(X))(Y-E(Y))]}{\sqrt{D(X)} \sqrt{D(Y)}}=\frac{\sum_{i=1}^n (X_i-\mu_X)(Y_i-\mu_Y)}{\sqrt{\sum_{i=1}^n(X_i-\mu_X)^2}*\sqrt{\sum_{i=1}^n(Y_i-\mu_Y)^2}}$

$dist(X,Y)=1-\rho_{XY}$
Pearson相关系数是统计学三大相关系数之一，具体内容可以参考《如何理解皮尔逊相关系数（Pearson Correlation Coefficient）？》

常见聚类算法

常见的算法，按照不同的思想可进行以下划分，当然还会有一些相应的优化算法，随后的博客也会一一介绍。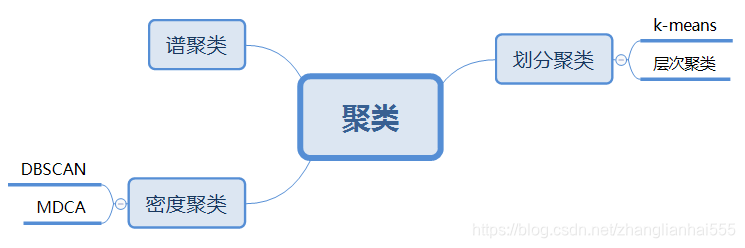
但，实际中，用的比较多的是划分聚类，尤其k-means。在古典目标识别中，经常用到Selective Search（选择搜索）这种图像bouding boxes提取算法，本质就是层次聚类。