浅谈KNN算法与KD树
什么是KNN?
我们先来看看KNN的英文全称: . 翻译过来就是K最近的邻居。KNN是一种分类算法,是数据挖掘分类技术中最简单的方法之一。所谓K最近邻,就是k个最近的邻居的意思,说的是每个样本都可以用它最接近的k个邻居来代表。
KNN的核心思想
kNN算法的核心思想是如果一个样本在特征空间中的k个最相邻的样本中的大多数属于某一个类别,则该样本也属于这个类别,并具有这个类别上样本的特性。该方法在确定分类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。 kNN方法在类别决策时,只与极少量的相邻样本有关。由于kNN方法主要靠周围有限的邻近的样本,而不是靠判别类域的方法来确定所属类别的,因此对于类域的交叉或重叠较多的待分样本集来说,kNN方法较其他方法更为适合。
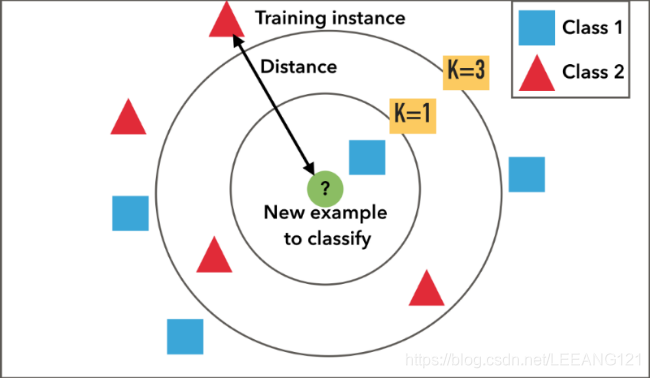
以上图为例:
我们判断绿色是属于类别1(蓝色方块)还是属于类别2(红色三角)
当K=1时即为K最近邻,此时搜索范围内类别1占比100%,判断绿色圆圈属于类别1;
当k=3时,类别2占比2/3,判断绿色圆圈属于类别2
一句话总结:近朱者赤,近墨者黑
KNN的算法流程
1.准备数据,对数据进行预处理
2. 选用合适的数据结构存储训练数据和测试元组
3. 设定参数,如k
4.维护一个大小为k的的按距离由大到小的优先级队列,用于存储最近邻训练元组。随机从训练元组中选取k个元组作为初始的最近邻元组,分别计算测试元组到这k个元组的距离,将训练元组标号和距离存入优先级队列
5. 遍历训练元组集,计算当前训练元组与测试元组的距离,将所得距离L 与优先级队列中的最大距离Lmax
6. 进行比较。若L>=Lmax,则舍弃该元组,遍历下一个元组。若L < Lmax,删除优先级队列中最大距离的元组,将当前训练元组存入优先级队列。
7. 遍历完毕,计算优先级队列中k 个元组的多数类,并将其作为测试元组的类别。
8. 测试元组集测试完毕后计算误差率,继续设定不同的k值重新进行训练,最后取误差率最小的k 值。
KNN的三要素
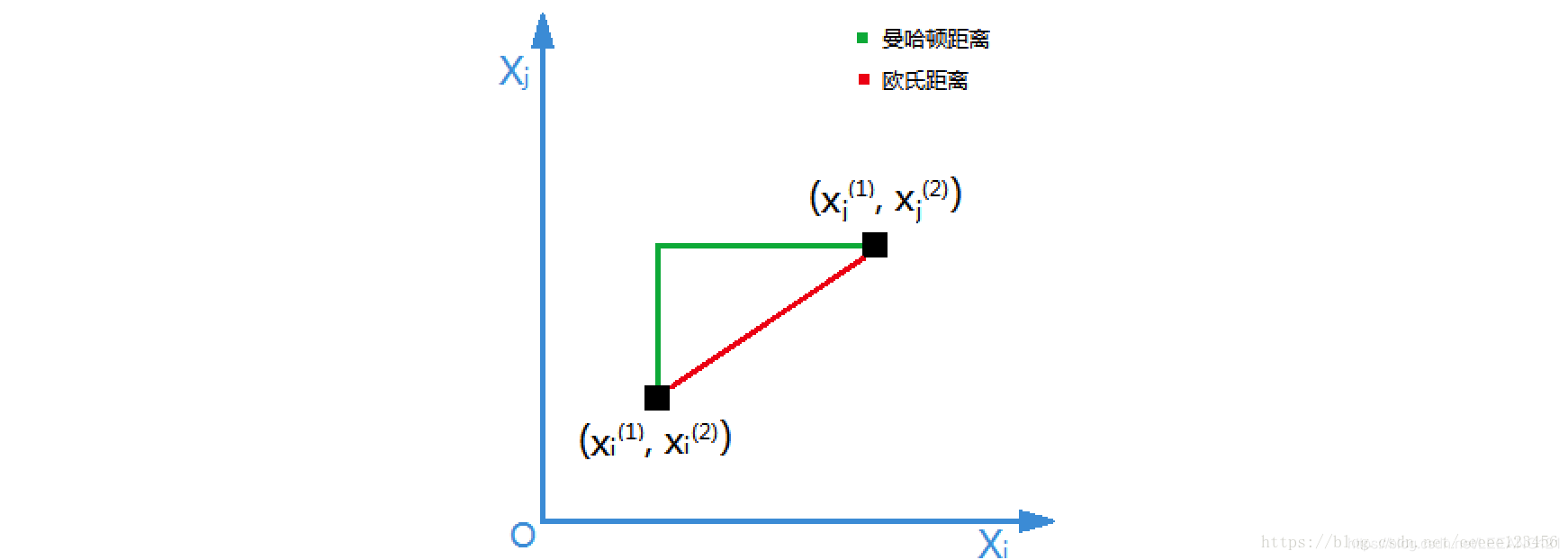
距离度量、k值的选择及分类决策规则是k近邻法的三个基本要素。根据选择的距离度量(如曼哈顿距离或欧氏距离),可计算测试实例与训练集中的每个实例点的距离,根据k值选择k个最近邻点,最后根据分类决策规则将测试实例分类。
度量距离
K值的选择
如果选择较小的K值,就相当于用较小的邻域中的训练实例进行预测,学习的近似误差会减小,只有与输入实例较近的训练实例才会对预测结果起作用,单缺点是学习的估计误差会增大,预测结果会对近邻的实例点分成敏感。如果邻近的实例点恰巧是噪声,预测就会出错。换句话说,K值减小就意味着整体模型变复杂,分的不清楚,就容易发生过拟合。
如果选择较大K值,就相当于用较大邻域中的训练实例进行预测,其优点是可以减少学习的估计误差,但近似误差会增大,也就是对输入实例预测不准确,K值得增大就意味着整体模型变的简单。
近似误差:可以理解为对现有训练集的训练误差。
估计误差:可以理解为对测试集的测试误差。
近似误差关注训练集,如果k值小了会出现过拟合的现象,对现有的训练集能有很好的预测,但是对未知的测试样本将会出现较大偏差的预测。模型本身不是最接近最佳模型。
分类决策规则
k近邻法中的分类决策规则往往是多数表决,即由输入实例的k个邻近的训练实例中的多数类,决定输入实例的类。
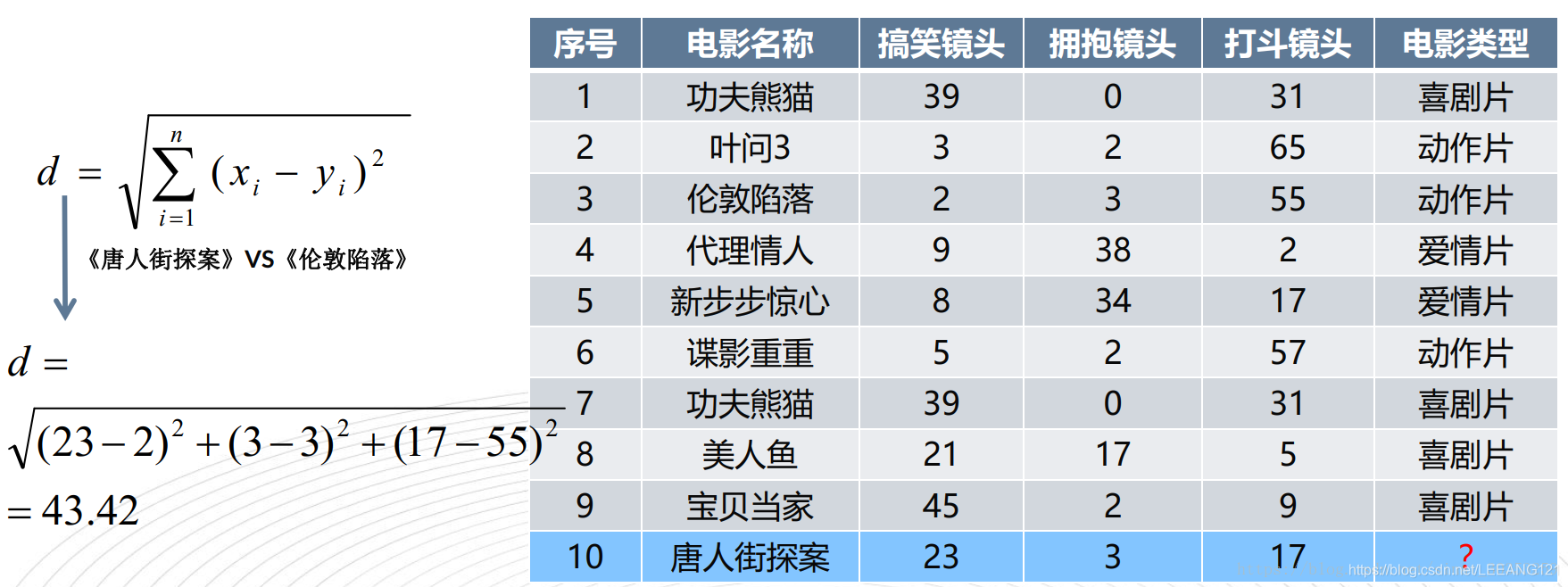
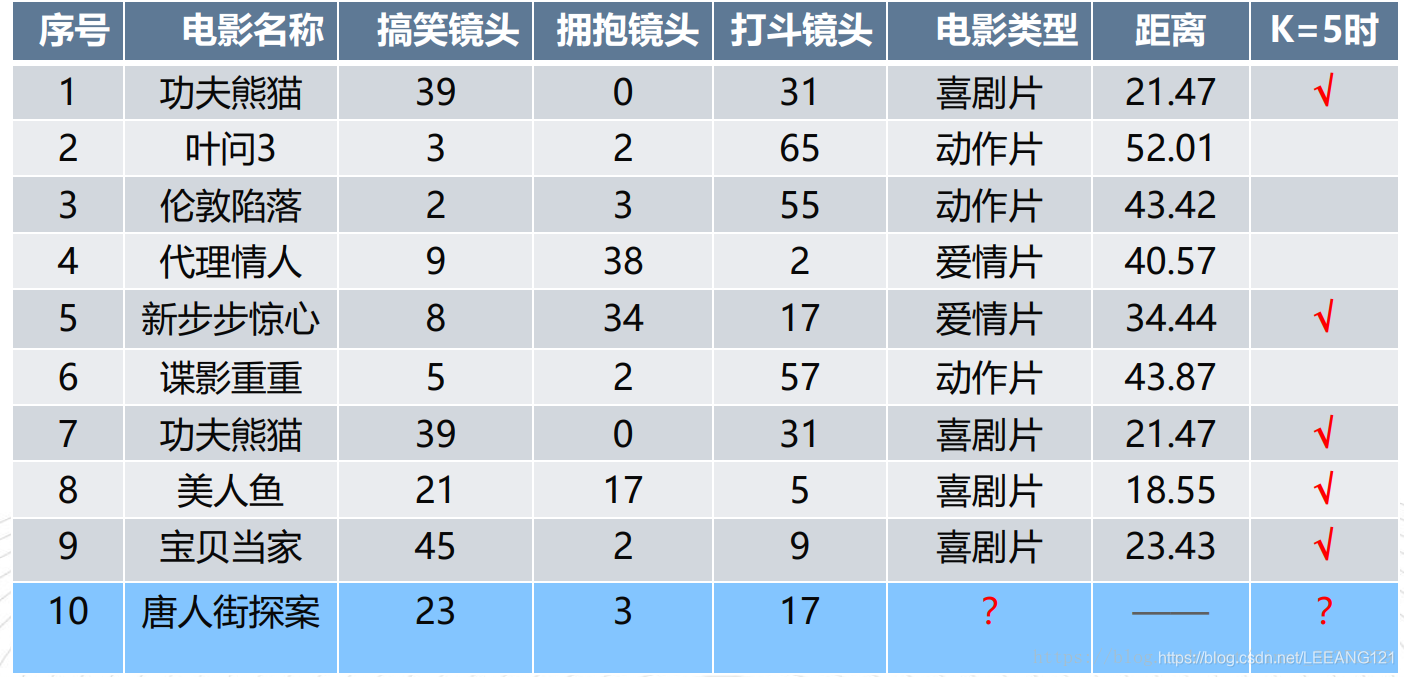
如上图所示,我们将唐人街探案这部电影作为我们要去分类的对象,第一幅图给出了如何计算两个节点之间的距离的方法,第二幅图利用该方法得出了唐人街探案与其他样本的距离,我们找到距离最近的5部影片,这5部影片有4部属于喜剧,因此我们把唐人街探案这部电影归结为喜剧电影。
什么是Kd-Tree?
实现k近邻法时,主要考虑的问题是如何对训练数据进行快速k近邻搜索,这点在特征空间的维数大及训练数据容量大时尤其必要。
k近邻法最简单的实现方法是线性扫描(linear scan),这时要计算输入实例与每一个训练实例的距离,当训练集很大时,计算非常耗时。为了提高k近邻法搜索的效率,可以考虑使用特殊的结构存储训练数据,以减少计算距离的次数。具体方法很多,kd树方法(kd树是存储k维空间数据的树结构,这里的k与k近邻法的k意义不同)就是其中一种。
原理
k-d树是每个节点都为k维点的二叉树。所有非叶子节点可以视作用一个超平面把空间分割成两个半空间。节点左边的子树代表在超平面左边的点,节点右边的子树代表在超平面右边的点。选择超平面的方法如下:每个节点都与k维中垂直于超平面的那一维有关。因此,如果选择按照x轴划分,所有x值小于指定值的节点都会出现在左子树,所有x值大于指定值的节点都会出现在右子树。这样,超平面可以用该x值来确定,其法线为x轴的单位向量。
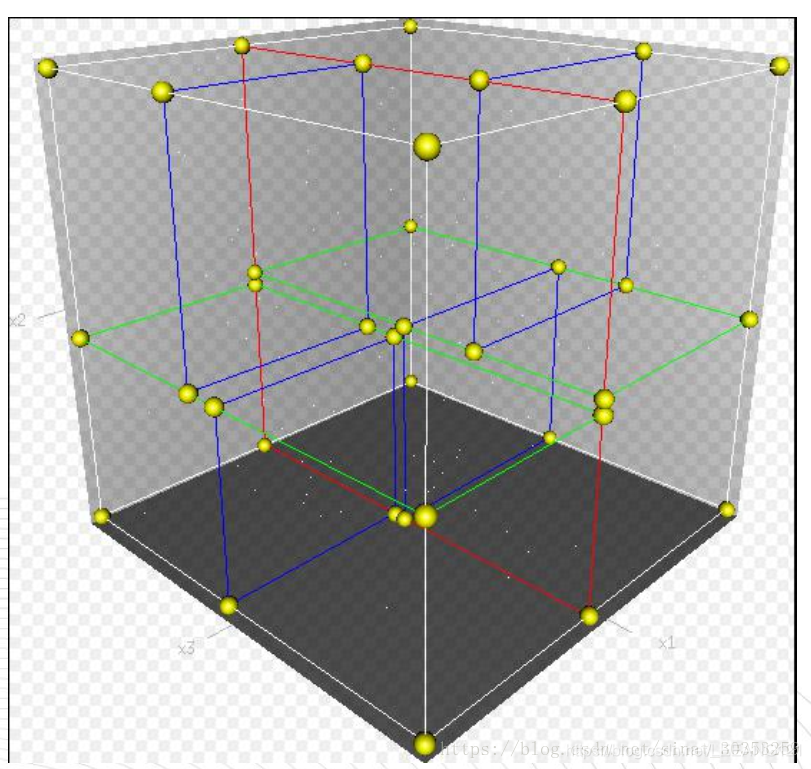
划分过程:
一个三维k-d树。 第一次划分(红色)把根节点(白色)划分成两个节点,然后它们分别再次被划分(绿色) 为两个子节点。最后这四个子节点的每一个都被划分(蓝色) 为两个子节点。 因为没有更进一步的划分, 最后得到的八个节点称为叶子节点。
上面的图像可能比较抽象,我们老规矩,举个栗子先:
假设有6个二维数据点{(2,3),(5,4),(9,6),(4,7),(8,1),(7,2)},数据点位于二维空间内(如下图中黑点所示)。kd树算法就是要确定图1中这些分割空间的分割线(多维空间即为分割平面,一般为超平面)。下面就要通过一步步展示kd树是如何确定这些分割线的。
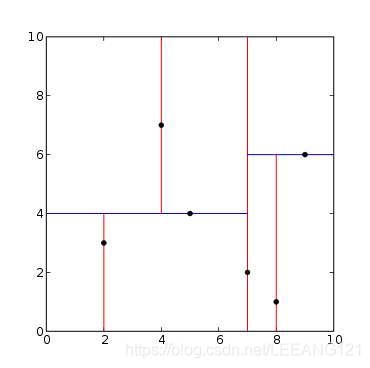
1、分别计算x,y方向上数据的方差,得知x方向上的方差最大;
2、根据x轴方向的值2,5,9,4,8,7排序选出中值为7,所以该node中的data = (7,2)。这样,该节点的分割超平面就是通过(7,2)并垂直于x轴的直线x = 7;
3、确定左子空间和右子空间。分割超平面x = 7将整个空间分为两部分,如下图所示。x < = 7的部分为左子空间,包含3个节点{(2,3),(5,4),(4,7)};另一部分为右子空间,包含2个节点{(9,6),(8,1)}。
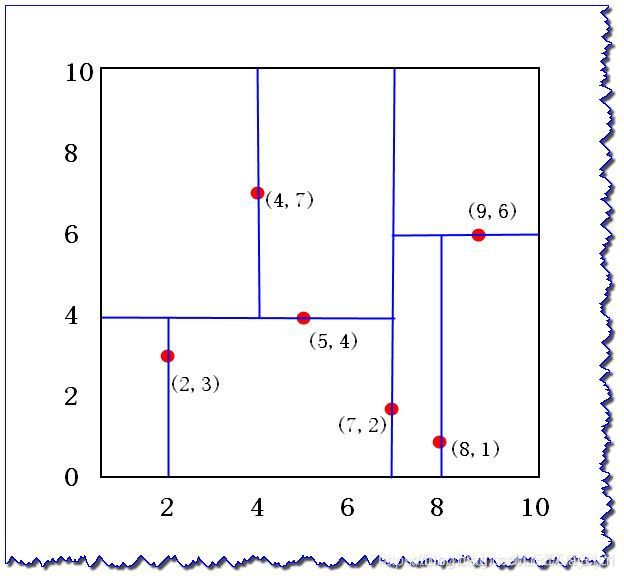
划重点:上图划分的第一条线段是过点(7,2)的竖直线段,划分完该线段后,数据集分了左右。此时重复步骤1,2和3即可以画出其余线段。
k-d树的构建是一个递归的过程。然后对左子空间和右子空间内的数据重复根节点的过程就可以得到下一级子节点(5,4)和(9,6)(也就是左右子空间的’根’节点),同时将空间和数据集进一步细分。如此反复直到空间中只包含一个数据点,如下图所示:
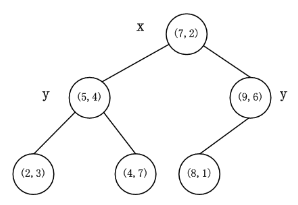
Kd-Tree的最近邻查找
(1)将查询数据Q从根结点开始,按照Q与各个结点的比较结果向下访问Kd-Tree,直至达到叶子结点。 其中Q与结点的比较指的是将Q对应于结点中的k维度上的值与中值m进行比较,若Q(k) < m,则访问左子树,否则访问右子树。达到叶子结点时,计算Q与叶子结点上保存的数据之间的距离,记录下最小距离对应的数据点,记为当前最近邻点nearest和最小距离dis。
(2)进行回溯操作,该操作是为了找到离Q更近的“最近邻点”。即判断未被访问过的分支里是否还有离Q更近的点,它们之间的距离小于dis。
如果Q与其父结点下的未被访问过的分支之间的距离小于dis,则认为该分支中存在离P更近的数据,进入该结点,进行(1)步骤一样的查找过程,如果找到更近的数据点,则更新为当前的最近邻点nearest,并更新dis。
如果Q与其父结点下的未被访问过的分支之间的距离大于dis,则说明该分支内不存在与Q更近的点。 回溯的判断过程是从下往上进行的,直到回溯到根结点时已经不存在与P更近的分支为止。
注:判断未被访问过的树分支中是否还有离Q更近的点,就是判断"Q与未被访问的树分支的距离|Q(k) - m|“是否小于"Q到当前的最近邻点nearest的距离dis”。从几何空间上来看,就是判断以Q为中心,以dis为半径超球面是否与未被访问的树分支代表的超矩形相交。
举个栗子
查找点Q(2.1,3.1)
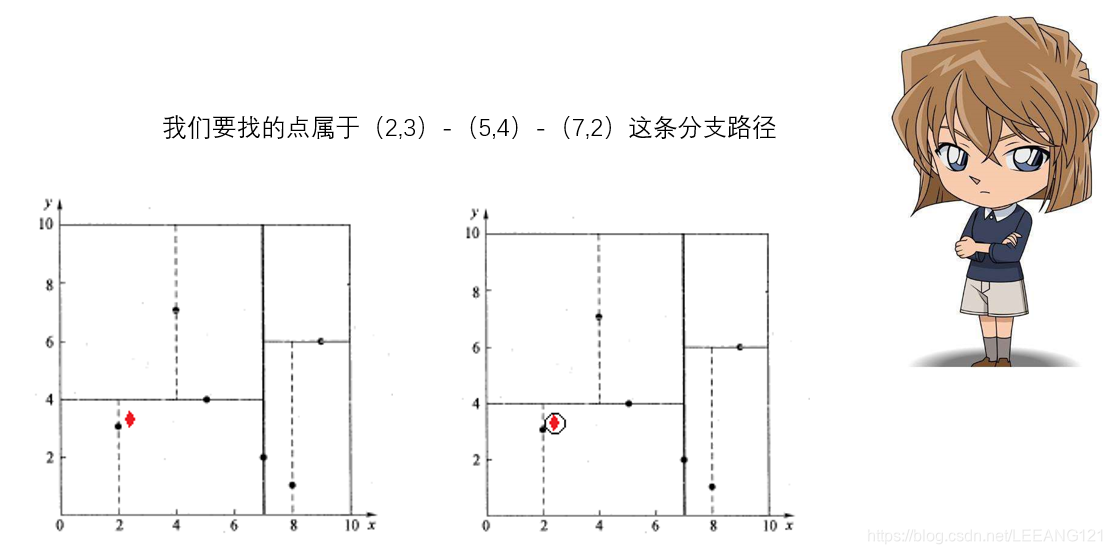
如下图所示,红色的点即为要查找的点。通过图4二叉搜索,顺着搜索路径很快就能找到当前的最邻近点(2,3)。
在上述搜索过程中,产生的搜索路径节点有<(7,2),(5,4),(2,3)>。为了找到真正的最近邻,还需要进行’回溯’操作,首先以(2,3)作为当前最近邻点nearest,计算其到查询点Q(2.1,3.1)的距离dis为0.1414,然后回溯到其父节点(5,4),并判断在该父节点的其他子节点空间中是否有距离查询点Q更近的数据点。以(2.1,3.1)为圆心,以0.1414为半径画圆,如图6所示。发现该圆并不和超平面y = 4交割,即这里:|Q(k) - m|=|3.1 - 4|=0.9 > 0.1414,因此不用进入(5,4)节点右子空间中去搜索。
再回溯到(7,2),以(2.1,3.1)为圆心,以0.1414为半径的圆更不会与x = 7超平面交割,因此不用进入(7,2)右子空间进行查找。至此,搜索路径中的节点已经全部回溯完,结束整个搜索,返回最近邻点(2,3),最近距离为0.1414。
总结
Kd树在维度较小时(比如20、30),算法的查找效率很高,然而当数据维度增大(例如:K≥100),查找效率会随着维度的增加而迅速下降。假设数据集的维数为D,一般来说要求数据的规模N满足N>>2的D次方,才能达到高效的搜索。 为了能够让Kd树满足对高维数据的索引,Jeffrey S. Beis和David G. Lowe提出了一种改进算法——Kd-tree with BBF(Best Bin First),该算法能够实现近似K近邻的快速搜索,在保证一定查找精度的前提下使得查找速度较快。