KNN—Kd树—BBF优化

一、KD树基本解释

1.1、基础概念

为了优化KNN的计算，使用KD树解决通过距离函数在高维矢量之间进行相似性检索的问题，快速而准确地找到查询点的近邻。

索引结构中相似性查询：: 范围查询：给定查询点和查询距离阈值，从数据集中查找所有与查询点距离小于阈值的数据; K近邻查询：给定查询点及正整数K，从数据集中找到距离查询点最近的K个数据，当K=1时，它就是最近邻查询。
$~$
特征点匹配：: 线性扫描/穷举搜索：依次计算样本集E中每个样本到输入实例点的距离，然后抽取出计算出来的最小距离的点即为最近邻点。
此种办法简单，但当样本集或训练集很大时。在物体识别的问题中，可能有数千个甚至数万个SIFT特征点，而去计算这成千上万的特征点与输入实例点的距离，时间复杂度高。; 构建数据索引: 因为实际数据一般都会呈现簇状的聚类形态，因此我们想到建立数据索引，然后再进行快速匹配。
索引树是一种树结构索引方法，其基本思想是对搜索空间进行层次划分。根据划分的空间是否有混叠可以分为Clipping和Overlapping两种。
前者划分空间没有重叠，其代表就是k-d树；后者划分空间相互有交叠，其代表为R树。

这里写图片描述

1.2 KD树的构建

域名	数据类型	描述
Node-data	数据矢量	数据集中某一个n维数据点，分割超面是通过数据点Node-Data并垂直于轴
Range	空间矢量	该节点所代表的空间范围
split	整数	垂直于分割超平面的方向轴序号。 split的平面，分割超面将整个空间分割成两个子空间。
令split域的值为i	/	如果空间Range中某个数据点的第i维数据小于Node-Data[i]，那么，它就属于该节点空间的左子空间，否则就属于右子空间。
Left /Right	k-d树	由位于该节点分割超平面左子空间/右子空间内所有数据点所构成的k-d树
parent	k-d树	父节点

1.3 算法的实现

输入：数据点集Data-set和其所在的空间Range
输出：Kd，类型为k-d tree 

1、If Data-set为空，则返回空的k-d tree
2、调用节点生成程序：   
  （1）确定split域：对于所有描述子数据（特征矢量），统计它们在每个维上的数据方差。 
      以SURF特征为例，描述子为64维，可计算64个方差。挑选出最大值，对应的维就是split域的值。 
      数据方差大表明沿该坐标轴方向上的数据分散得比较开，在这个方向上进行数据分割有较好的分辨率；
  （2）确定Node-data域：数据点集Data-set按其第split域的值排序。 
      位于正中间的那个数据点被选为Node-data。 
      此时新的Data-set’ = Data-set\Node-data（除去其中Node-data这一点）。

3、dataleft = {d属于Data-set’ && d[split] ≤ Node-data[split]}Left_Range =  
  {Range && dataleft} dataright = {d属于Data-set’ && d[split] > Node-data[split]}Right_Range  
  = {Range && dataright}

4.eft = 由（dataleft，Left_Range）建立的k-d tree， 
即递归调用createKDTree（dataleft，Left_Range）。并设置left的parent域为Kd； 
right = 由（dataright，Right_Range）建立的k-d tree， 
即调用createKDTree（dataright，Right_Range）。并设置right的parent域为Kd。

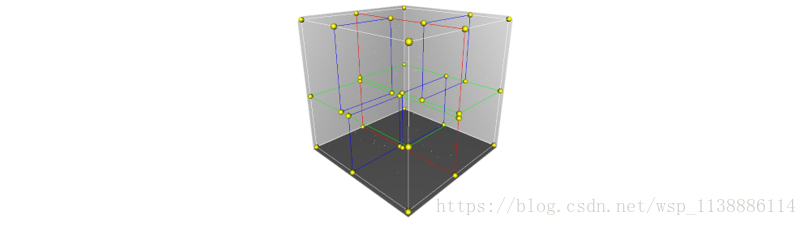
实例：k-d树构建算法。: 假设有6个二维数据点{(2,3)，(5,4)，(9,6)，(4,7)，(8,1)，(7,2)}，数据点位于二维空间内，如下图所示。
为了能有效的找到最近邻，k-d树采用分而治之的思想，即将整个空间划分为几个小部分，
首先，粗黑线将空间一分为二，然后在两个子空间中，细黑直线又将整个空间划分为四部分，最后虚黑直线将这四部分进一步划分。

这里写图片描述

具体步骤

1、确定：split域=x。具体是：6个数据点在x，y维度上的数据方差分别为39，28.63，所以在x轴上方差更大，故split域值为x；
2、确定：Node-data = （7,2）。具体是：根据x维上的值将数据排序，6个数据的中值(所谓中值，即中间大小的值)为7， 
   所以Node-data域位数据点（7,2）。这样，该节点的分割超平面就是通过（7,2）并垂直于：split=x轴的直线x=7；
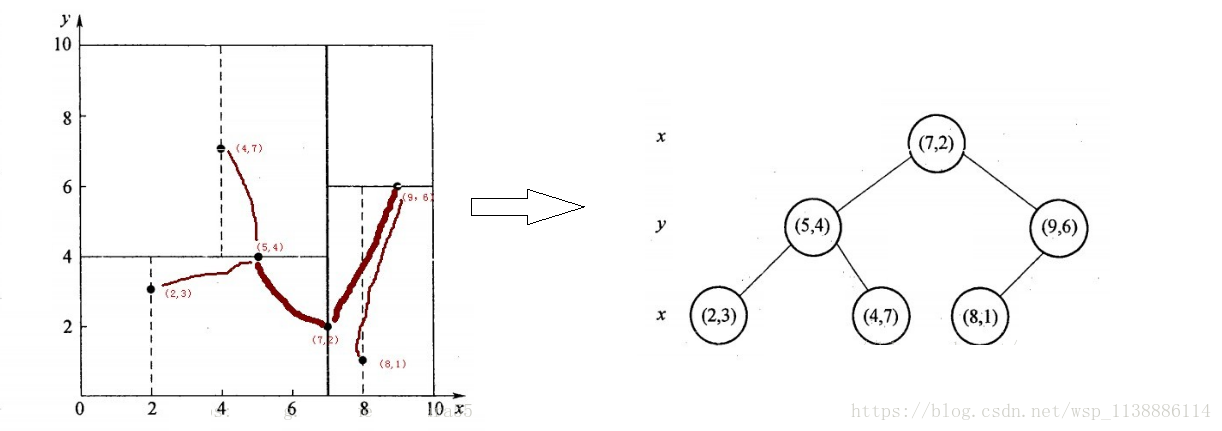
3、确定：左子空间和右子空间。具体是：分割超平面x=7将整个空间分为两部分：x<=7的部分为左子空间， 
   包含3个节点={(2,3),(5,4),(4,7)}；另一部分为右子空间，包含2个节点={(9,6)，(8,1)}；
   与此同时，经过对上面所示的空间划分之后，我们可以看出，点(7,2)可以为根结点， 
   从根结点出发的两条红粗斜线指向的(5,4)和(9,6)则为根结点的左右子结点，而(2,3)，(4,7)则为(5,4)的左右孩子(通过两条细红斜线相连)， 
   最后，(8,1)为(9,6)的左孩子(通过细红斜线相连)。如此，便形成了下面这样一棵k-d树

二、KD树基本操作

2.1、KD树查找

KD树的查找算法：: 在k-d树中进行数据的查找也是特征匹配的重要环节，其目的是检索在k-d树中与查询点距离最近的数据点。对于kd树的检索，其具体过程为：
● 从根节点开始，将待检索的样本划分到对应的区域中（在kd树形结构中，从根节点开始查找，直到叶子节点，将这样的查找序列存储到栈中）
● 以栈顶元素与待检索的样本之间的距离作为最短距离min_distance
● 执行出栈操作：
◆ 向上回溯，查找到父节点，若父节点与待检索样本之间的距离小于当前的最短距离min_distance，则替换当前的最短距离min_distance
◆ 以待检索的样本为圆心（二维，高维情况下是球心），以min_distance为半径画圆，若圆与父节点所在的平面相割，则需要将父节点的另一棵子树进栈，重新执行以上的出栈操作
● 直到栈为空
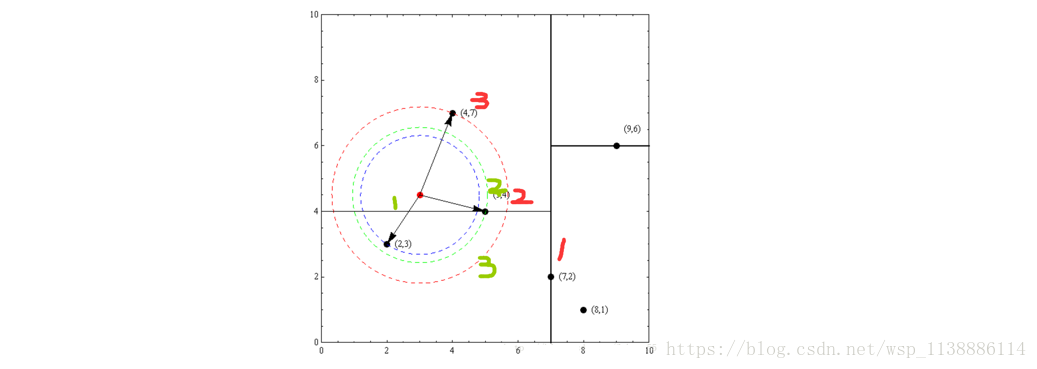
举例: 以先前构建好的kd树为例，查找目标点（3,4.5）的最近邻点。
同样先进行二叉查找，先从（7,2）查找到（5,4）节点，在进行查找时是由y = 4为分割超平面的，
由于查找点为y值为4.5，因此进入右子空间查找到（4,7），
形成搜索路径： （7,2）→（5,4）→（4,7）。
取（4,7）为当前最近邻点。以目标查找点为圆心，目标查找点到当前最近点的距离2.69为半径确定一个红色的圆。
然后回溯到（5,4），计算其与查找点之间的距离为2.06，则该结点比当前最近点距目标点更近，以(5,4)为当前最近点。
用同样的方法再次确定一个绿色的圆，可见该圆和y = 4超平面相交，所以需要进入（5,4）结点的另一个子空间进行查找。
（2,3）结点与目标点距离为1.8，比当前最近点要更近，所以最近邻点更新为（2，3），最近距离更新为1.8，同样可以确定一个蓝色的圆。
接着根据规则回退到根结点(7,2)，蓝色圆与x=7的超平面不相交，因此不用进入（7,2）的右子空间进行查找。
至此，搜索路径回溯完，返回最近邻点（2,3），最近距离1.8。; 如果实例点是随机分布的，kd树搜索的平均计算复杂度是O(logN)O(logN)，这里N是训练实例数。kd树更适用于训练实例数远大于空间维数时的k近邻搜索。 当空间维数接近训练实例数时，它的效率会迅速下降，几乎接近线性扫描。

从上述标准的kd树查询过程可以看出其搜索过程中的“回溯”是由“查询路径”决定的，并没有考虑查询路径上一些数据点本身的一些性质。一个简单的改进思路就是将“查询路径”上的结点进行排序，如按各自分割超平面（也称bin）与查询点的距离排序，也就是说，回溯检查总是从优先级最高（Best Bin）的树结点开始。

具体步骤和思路如下：: ● 在某一层，分割面是第ki维，分割值是kv，那么 abs(q[ki]-kv) 就是没有选择的那个分支的优先级，也就是计算的是那一维上的距离；
● 同时，从优先队列里面取节点只在某次搜索到叶节点后才发生，计算过距离的节点不会出现在队列的，比如1~10这10个节点，你第一次搜索到叶节点的路径是1-5-7，那么1，5，7是不会出现在优先队列的。换句话说，优先队列里面存的都是查询路径上节点对应的相反子节点，
比如：
搜索左子树，就把对应这一层的右节点存进队列。
此算法能确保优先检索包含最近邻点可能性较高的空间，此外，BBF机制还设置了一个运行超时限定。采用了BBF查询机制后，kd树便可以有效的扩展到高维数据集上。
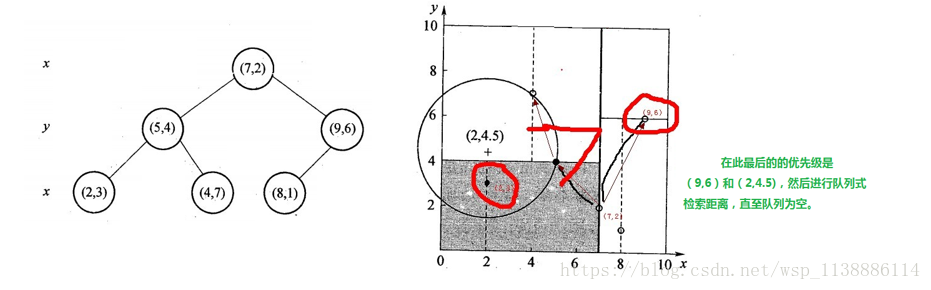
事例: 1、将（7,2）压入优先队列中；
2、提取优先队列中的（7,2），由于（2,4.5）位于（7,2）分割超平面的左侧，所以检索其左子结点（5,4）。
同时，根据BBF机制”搜索左/右子树，就把对应这一层的兄弟结点即右/左结点存进队列”，将其（5,4）对应的兄弟结点即右子结点（9,6）压人优先队列中，此时优先队列为{（9,6）}，最佳点为（7,2）；
然后一直检索到叶子结点（4,7），此时优先队列为{（2,3），（9,6）}，“最佳点”则为（5,4）；
3、提取优先级最高的结点（2,3），重复步骤2，直到优先队列为空。