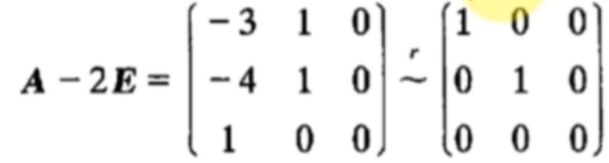线代：1.6矩阵的特征值和特征向量

本课程来自 深度之眼，部分截图来自课程视频。
【第一章 线性代数】1.6矩阵的特征值和特征向量
在线LaTeX公式编辑器

任务详解：

1、掌握内积，正交，线性相关，线性无关的概念
2、掌握规范正交基，正交矩阵
3、掌握特征值特征向量的几何意义与算法

1.向量的内积和范数

向量的内积以及正交性

定义1:

设有n维向量(如果不做特殊说明，n维向量都是指列向量)

[x，y]称为向量x与y的内积(或者叫点积，elementwise).
内积是两个向量之间的一种运算，其结果是一个实数，用矩阵记号表示，当x与y都是列向量时，有
$[x,y]=x^Ty=y^Tx$
有时候也记做：<x,y>

还有一个重要性质：柯西不等式
$[x,y]^2≤[x,x][y,y]$

由以上性质加上我们中学在二维空间里面向量夹角的概念，我们可以推广到高维空间，也可以用来衡量高维空间中两个样本的相似度的一种度量（不同于欧式距离）。

定义2

令
$||x||=\sqrt{[x,x]}=\sqrt{x_1^2+x_2^2+...+x_n^2}$
$||x||$称为n维向量x的长度或者范数或者模长
当 $||x||=1$时，称x为单位向量。
向量的长度具有下述性质：
（i）非负性：当x≠0时， $||x||>0$；当x=0时， $||x||=0$；
（i）齐次性： $|\lambda x|=|\lambda|||x||$；右边的实数外面是绝对值
（ii）三角不等式： $||x+y||≤||x||+||y||$。
当[x，y]=0时，称向量x与y正交（二维上看就在垂直关系）.显然，若x=0，则x与任何向量都正交。

定理1：若n维向量 $a_1,a_2,…,a_n$是一组两两正交的非零向量（ $[a_i,a_j]=0,i\neq j$），则 $a_1,a_2,…,a_n$线性无关.
以下是百度百科中的线性无关定义：
在向量空间V的一组向量A: $a_1, a_2, ···,a_m$如果存在不全为零的数 $k_1, k_2, ···,k_m$ , 使
$k_1a_1+k_2a_2+...+k_ma_m=0$
则称向量组A是线性相关的 ，否则数 $k_1, k_2, ···,k_m$全为0时，称它是线性无关。
由此定义看出 是否线性相关，就看是否存在一组不全为零的数 $k_1, k_2, ···,k_m$使得上式成立。
定理1证明：
在式子 $k_1a_1+k_2a_2+...+k_ma_m=0$的左右两边同时点乘 $a_1$得
$k_1[a_1,a_1]+k_2[a_2,a_1]+...+k_m[a_m,a_1]=0$
由于 $a_1,a_2,…,a_m$两两正交，因此： $[a_2,a_1]=0,...[a_m,a_1]=0$
$k_1[a_1,a_1]=0$，由条件可知 $a_1$是非零向量，[a_1,a_1]≠0，
因此 $k_1=0$，同理 $k_2=0, ···,k_m=0$
$a_1,a_2,…,a_n$线性无关.得证。

定义3

设n维向量 $e_1,e_2,…,e_r$，是向量空间 $V(V\subset R^n)$的一个基，如果 $e_1,e_2,…,e_r$两两正交，且都是单位向量，则称 $e_1,e_2,…,e_r$是V的一个规范正交基。例如：

就是 $R^4$的一个规范正交基.
若 $e_1,e_2,…,e_r$是V的一个规范正交基，那么V中任一向量a应能由 $e_1,e_2,…,e_r$线性表示，设表示式为
$a=\lambda_1 e_1+\lambda_2e_2+,…,+\lambda_re_r$
$\lambda_r=[a,e_r]$

定义4

如果n阶矩阵A满足
$A^TA=E,即A^{-1}=A^T$
那么称A为正交矩阵，简称正交阵。
上式用列向量表示，即是
$\begin{bmatrix} a_1^T\\a_2^T \\ \vdots \\a_n^T \end{bmatrix}(a_1,a_2,\cdots,a_n)=E$
因为 $A^TA=E$与 $AA^T=E$等价，所以上述结论对A的行向量也成立。
由此可见，你、阶正交阵A的n个列（或者行）向量构成的向量空间 $\real^n$的一个规范正交基。

判定矩阵A可逆的小结

1、A的行列式不等于0
2、A的秩等于A的维度n
3、 $a_1,a_2,…,a_n$线性无关

2.特征值特征向量以及矩阵的相似

方阵的特征值与特征向量

定义6

设A是n阶矩阵，如果数λ和μ维非零列向量x使下面关系式成立，
$Ax=\lambda x$
那么，这样的数λ称为矩阵A的特征值，非零向量x称为A的对应于特征值λ的特征向量。
人话版本（物理意义）：刚开始讲矩阵的时候，讲过矩阵的本质是对应线性变换，如果从线性变换的角度看待这个问题，那么就是：现在我们有一个可以做线性变换的矩阵A，如果有一个向量x（注意不是变量），通过这个矩阵进行线性变换（就是乘上A）后的到 $\tilde x$相对于原来的x方向不变，仅仅是大小变化而已（变大了λ倍），（说明这个x还蛮特殊的，一般的向量经过线性变换后大小方向都会变化）那么就把这个特殊的x叫做A的特征向量，变大的倍数λ称为特征值。
如果给我们一个A，如何来求特征值λ和特征向量x呢？就是把上面的公式 $Ax=\lambda x$解方程，把x提取出来，x向量提取出来后，还剩下单位向量E，变成下面的公式：
$(A-\lambda E)x=0$
根据之前学过的克莱姆法则（如果 $Ax=0$有非零解，则|A|=0,如果是|A|≠0则方程只有唯一解，那么x只能=0），则要使得上面的式子要有非零解的充分必要条件是 $|A-\lambda E|=0$：
$\begin{vmatrix} a_{11}-\lambda& a_{12}&\cdots & a_{1n}\\ a_{21}& a_{22}-\lambda&\cdots & a_{2n}\\ \vdots& \vdots&& \vdots\\ a_{n1}& a_{n2}&\cdots & a_{nn}-\lambda \end{vmatrix}=0$
把上面的式子看做是关于λ的方程 $f(\lambda)=0$
(i) $\lambda_1+\lambda_2+\cdots+\lambda_n=a_{11}+a_{22}+\cdots+a_{nn}$
(II) $\lambda_1\lambda_2\cdots\lambda_n=|A|$
设 $\lambda=\lambda_i$为矩阵A的一个特征值，则由方程
$(A-\lambda_iE)x=0$
可求得非零解 $x=p_i$，那么 $p_i$便是A的对应于特征值 $\lambda_i$的特征向量。
例子：求矩阵 $A=\begin{bmatrix} 3 & -1\\ -1& 3 \end{bmatrix}$的特征值和特征向量。
解：先求 $|A-\lambda E|=\begin{vmatrix} 3-\lambda & -1\\ -1& 3-\lambda \end{vmatrix}=(3-\lambda)^2-1=0$
$3-\lambda=\pm 1$求得两个特征值： $\lambda_1=2,\lambda_2=4$
分两步
第一步求 $\lambda_1=2$对应的特征向量，解下面方程
$(A-\lambda_1 E)x_1=0$
$\begin{bmatrix} 3-\lambda_1 & -1\\ -1& 3-\lambda_1 \end{bmatrix}x_1=0$
$\begin{bmatrix} 1 & -1\\ -1& 1 \end{bmatrix}\begin{bmatrix}x_{11}\\x_{12}\end{bmatrix}=0$
解得： $x_1=\begin{bmatrix}1\\1\end{bmatrix}$归一化后得： $x_1=\begin{bmatrix}\frac{\sqrt{2}}{2}\\\frac{\sqrt{2}}{2}\end{bmatrix}$
第一步求 $\lambda_1=4$对应的特征向量，解下面方程
$(A-\lambda_1 E)x_2=0$
$\begin{bmatrix} 3-\lambda_2 & -1\\ -1& 3-\lambda_2 \end{bmatrix}x_2=0$
$\begin{bmatrix} -1 & -1\\ -1& -1 \end{bmatrix}\begin{bmatrix}x_{21}\\x_{22}\end{bmatrix}=0$
解得： $x_2=\begin{bmatrix}1\\-1\end{bmatrix}$归一化后得： $x_2=\begin{bmatrix}\frac{\sqrt{2}}{2}\\-\frac{\sqrt{2}}{2}\end{bmatrix}$
再看一例：
求矩阵 $A=\begin{bmatrix} -1& 1&0\\ -4& 3&0\\ 1 &0 &2 \end{bmatrix}$的特征值和特征向量。
解：A的特征多项式为
$|A-\lambda E|=\begin{vmatrix} -1-\lambda & 1&0\\ -4& 3-\lambda&0\\ 1 &0&2-\lambda \end{vmatrix}=(3-\lambda)^2-1=(2-\lambda)(1-\lambda)^2$
所以A的特征值为 $\lambda_1=2,\lambda_2=\lambda_3=1$
当 $\lambda_1=2$时，解方程 $(A-2E)x=0$.由

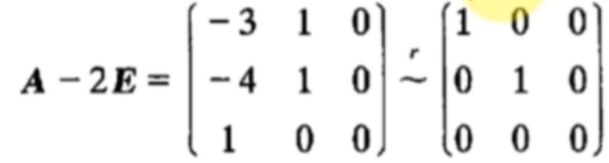
得基础解系： $p_1=\begin{bmatrix}0\\0\\1\end{bmatrix}$
所以 $kp_1(k\neq0)$是对应于 $\lambda_1=2$的全部特征向量。
另外一组解：
当 $\lambda_2=\lambda_3=1$时，解方程 $(A-2E)x=0$.由

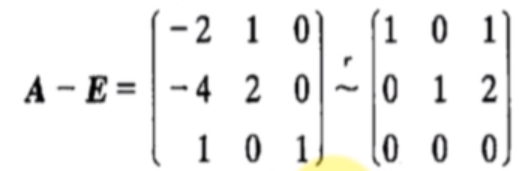
得基础解系： $p_2=\begin{bmatrix}-1\\-2\\1\end{bmatrix}$
所以 $kp_2(k\neq0)$是对应于 $\lambda_2=\lambda_3=1$的全部特征向量。
由于有重根，所以只要两个特征向量

例8设 $\lambda$是方阵A的特征值，证明
（1） $\lambda^2$是 $A^2$的特征值；
（2）当A可逆时， $\frac{1}{\lambda}$是 $A^{-1}$的特征值.
证明（1）：由 $\lambda$是方阵A的特征值可知： $Ax=\lambda x$
$A^2x=\lambda Ax=\lambda^2x$
以此类推： $A^n$的特征值为 $\lambda^n$，特征向量为x
n可以为负数，例如 $A^{-2}$的特征值为 $\lambda^{-2}$
证明（2）：由 $\lambda$是方阵A的特征值可知： $Ax=\lambda x$，两边同时乘以A的逆矩阵得：
$x=\lambda A^{-1}x$，两边同时除以 $\lambda$得
$\frac{1}{\lambda}x=A^{-1}x$，即 $A^{-1}x=\frac{1}{\lambda}x$，根据特征值的定义可知：
$\frac{1}{\lambda}$是 $A^{-1}$的特征值，特征向量为x
再推广：如果 $\lambda$是方阵A的特征值，那么 $f(\lambda)$是方阵 $f(A)$的特征值。
例子：设3阶矩阵A的特征值为1，-1,2，求 $A^2+3A-2E$的特征值。
解：把A的特征值1，-1,2分别代入上式
$1^2+3*1-2=2$
$(-1)^2+3(-1)-2=-4$
$2^2+3*2-2=8$
$A^2+3A-2E$的特征值为2，-4,8