剑指Offer #07 斐波那契数列（四种解法）| 图文详解

题目来源：牛客网-剑指Offer专题
题目地址：斐波那契数列

题目描述

大家都知道斐波那契数列，现在要求输入一个整数n，请你输出斐波那契数列的第n项（从0开始，第0项为0）。n<=39

题目解析

方法一：
普通递归版求法，这种方法通常和汉诺塔一起被放在课本的递归教学部分，应该是面试官不希望看到的算法。
$F(n) = \begin{cases} 0, & \text {n=0} \\ 1, & \text {n=1,2} \\ F(n-1)+F(n-2), & \text{n>2} \end{cases}$
利用上面递推式，自顶向下进行求解，因为存在大量的重叠子问题，时间复杂度为 $O(2^n)$。

public class Solution {
    public int Fibonacci(int n) {
        if (n == 0) return 0;
        if (n == 1) return 1;
        return Fibonacci(n - 1) + Fibonacci(n - 2);
    }
}

方法二：
我们可以将递推式的求解从自顶向下改为自底向上（循环实现）。简而言之，我们已知前两项的值，然后我们就可以用前两项的值求出第3项的值，接着求第4、第5、……，直到求出第n项的值。（废话）

实现过程如下图所示，两个相同颜色的箭头可以确定一个新的数列项。

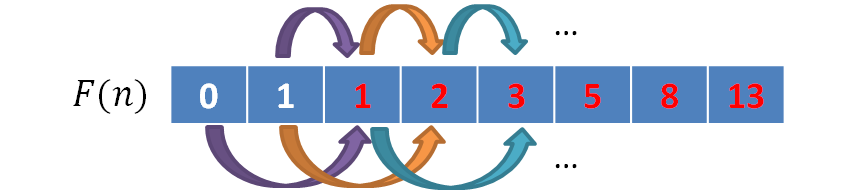
上述算法的时间复杂度为 $O(n)$，在面试中够用了，如果还是觉得简单可以继续往下看。

public class Solution {
    public int Fibonacci(int n) {
        int a = 0, b = 1;
        for (int i = 1; i <= n - 2; i++) {
            a = a + b;
            b = a - b;
        }
        return a;
    }
}

方法三：
我们知道：
$F(n)=F(n-1)+F(n-2) \\ F(n-1)=F(n-1)+0*F(n-2)$
将其转化成矩阵运算可得

$\begin{pmatrix} F(n) \\ F (n-1)\\ \end{pmatrix}= \begin{pmatrix} 1&1 \\ 1&0 \\ \end{pmatrix}* \begin{pmatrix} F(n-1) \\F(n-2)\\ \end{pmatrix}$
而右边的 $2\times1$阶矩阵又可以进一步分解为
$\begin{pmatrix} F(n-1) \\ F (n-2)\\ \end{pmatrix}= \begin{pmatrix} 1&1 \\ 1&0 \\ \end{pmatrix}* \begin{pmatrix} 1&1 \\ 1&0 \\ \end{pmatrix}* \begin{pmatrix} F(n-2) \\F(n-3)\\ \end{pmatrix}$
按照这样一直分解下去直到右边的 $2\times1$阶矩阵F(2),F(1),即
$\begin{pmatrix} F(n) \\ F (n-1)\\ \end{pmatrix}= \begin{pmatrix} 1&1 \\ 1&0 \\ \end{pmatrix}^{n-2}* \begin{pmatrix} F(2) \\F(1)\\ \end{pmatrix}$
这时利用矩阵版的快速幂求解其中的矩阵幂乘，就可以在 $O(logn)$ 的时间复杂度下得出Fibonacci数列的第n项的值。

这种方法通常是用在算法比赛中，在面试中容易装逼失败不适合使用，这里也不挂板子了。

方法四：
根据上面的递推式，利用我们高中学过的“待定系数法”可以推导出斐波那契数列的通项公式。公式如下，（推导过程略）
$F(n)=\frac {\sqrt5} {5} [(\frac {1+\sqrt5} {2})^n-(\frac {1-\sqrt5} {2})^n]$
公式法时间复杂度为 $O(1)$ ? 感觉不然，求公式中的 $n$ 次方应该要用上快速幂，我个人认为时间复杂度应该也是 $O(logn)$。（我要滚去看源码了 ）

public class Solution {
    public int Fibonacci(int n) {
        double a = Math.sqrt(5)/5;
        double b = Math.pow((1+ Math.sqrt(5))/2, n);
        double c = Math.pow((1- Math.sqrt(5))/2, n);
        return (int)(a * (b - c));
    }
}

后记:
如果你在写出循环版之后，再给面试官描述后面两种算法，并流畅写出通项公式的推导过程，相信肯定可以取得面试官的芳心~

---

如果本文对你有所帮助，要记得点赞哦~