参考伯禹学习平台《动手学深度学习》课程内容内容撰写的学习笔记
批量归一化(BatchNormalization)和残差网络
处理后的任意一个特征在数据集中所有样本上的均值为0、标准差为1。
利用小批量上的均值和标准差,不断调整神经网络中间输出,从而使整个神经网络在各层的中间输出的数值更稳定。本质上是标准化数据的处理
位置:全连接层中的仿射变换和激活函数之间。全连接:
x
=
W
u
+
b
o
u
t
p
u
t
=
ϕ
(
x
)
\boldsymbol{x} = \boldsymbol{W\boldsymbol{u} + \boldsymbol{b}} \\ output =\phi(\boldsymbol{x})
x = W u + b o u t p u t = ϕ ( x )
批量归一化(均值为0标准差为1):
o
u
t
p
u
t
=
ϕ
(
BN
(
x
)
)
output=\phi(\text{BN}(\boldsymbol{x}))
o u t p u t = ϕ ( BN ( x ) )
y
(
i
)
=
BN
(
x
(
i
)
)
\boldsymbol{y}^{(i)} = \text{BN}(\boldsymbol{x}^{(i)})
y ( i ) = BN ( x ( i ) )
μ
B
←
1
m
∑
i
=
1
m
x
(
i
)
,
\boldsymbol{\mu}_\mathcal{B} \leftarrow \frac{1}{m}\sum_{i = 1}^{m} \boldsymbol{x}^{(i)},
μ B ← m 1 i = 1 ∑ m x ( i ) ,
σ
B
2
←
1
m
∑
i
=
1
m
(
x
(
i
)
−
μ
B
)
2
,
\boldsymbol{\sigma}_\mathcal{B}^2 \leftarrow \frac{1}{m} \sum_{i=1}^{m}(\boldsymbol{x}^{(i)} - \boldsymbol{\mu}_\mathcal{B})^2,
σ B 2 ← m 1 i = 1 ∑ m ( x ( i ) − μ B ) 2 ,
x
^
(
i
)
←
x
(
i
)
−
μ
B
σ
B
2
+
ϵ
,
\hat{\boldsymbol{x}}^{(i)} \leftarrow \frac{\boldsymbol{x}^{(i)} - \boldsymbol{\mu}_\mathcal{B}}{\sqrt{\boldsymbol{\sigma}_\mathcal{B}^2 + \epsilon}},
x ^ ( i ) ← σ B 2 + ϵ
x ( i ) − μ B ,
这⾥ϵ > 0是个很小的常数,保证分母大于0
y
(
i
)
←
γ
⊙
x
^
(
i
)
+
β
.
{\boldsymbol{y}}^{(i)} \leftarrow \boldsymbol{\gamma} \odot \hat{\boldsymbol{x}}^{(i)} + \boldsymbol{\beta}.
y ( i ) ← γ ⊙ x ^ ( i ) + β .
引入可学习参数:拉伸参数γ和偏移参数β。若
γ
=
σ
B
2
+
ϵ
\boldsymbol{\gamma} = \sqrt{\boldsymbol{\sigma}_\mathcal{B}^2 + \epsilon}
γ = σ B 2 + ϵ
β
=
μ
B
\boldsymbol{\beta} = \boldsymbol{\mu}_\mathcal{B}
β = μ B
位置:卷积计算之后、应⽤激活函数之前。c p*q
训练:以batch为单位,对每个batch计算均值和方差。移动平均 估算整个训练数据集的样本均值和方差。
(何凯明2015imagenet图像识别赛里夺魁)
恒等映射:易于捕捉恒等映射的细微波动 )
在残差块中,输⼊x可通过跨层 的数据线路更快 地向前传播。 并没有对层做改变。
卷积(64,7x7,3)
残差块x4 (通过步幅为2的残差块在每个模块之间减小高和宽)
全局平均池化
全连接
用connect连结 A的通道数和B的通道数相加
###主要构建模块:
A inchannels 与B outchannels连结 输出inchannels+outchannels,在给Ainchannels+outchannels,循环
1
×
1
1\times1
1 × 1 减小模型复杂度
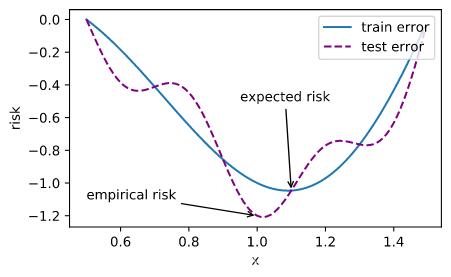
尽管优化方法可以最小化深度学习中的损失函数值,但本质上优化方法达到的目标与深度学习的目标并不相同。
优化方法目标:训练集损失函数值
深度学习目标:测试集损失函数值(泛化性)
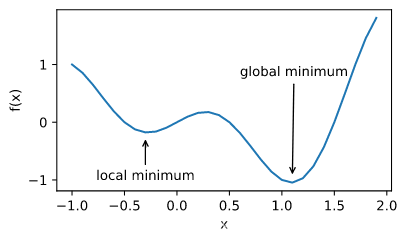
局部最小值
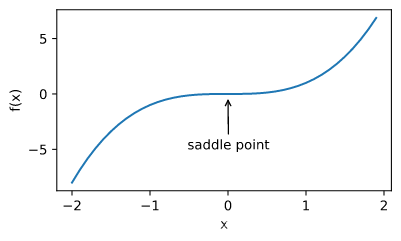
鞍点
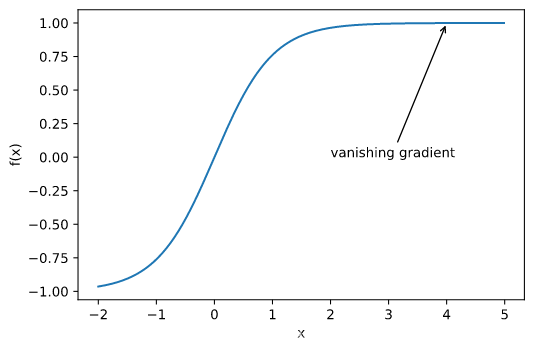
梯度消失
f
(
x
)
=
x
cos
π
x
f(x) = x\cos \pi x
f ( x ) = x cos π x
梯度为0
A
=
[
∂
2
f
∂
x
1
2
∂
2
f
∂
x
1
∂
x
2
⋯
∂
2
f
∂
x
1
∂
x
n
∂
2
f
∂
x
2
∂
x
1
∂
2
f
∂
x
2
2
⋯
∂
2
f
∂
x
2
∂
x
n
⋮
⋮
⋱
⋮
∂
2
f
∂
x
n
∂
x
1
∂
2
f
∂
x
n
∂
x
2
⋯
∂
2
f
∂
x
n
2
]
A=\left[\begin{array}{cccc}{\frac{\partial^{2} f}{\partial x_{1}^{2}}} & {\frac{\partial^{2} f}{\partial x_{1} \partial x_{2}}} & {\cdots} & {\frac{\partial^{2} f}{\partial x_{1} \partial x_{n}}} \\ {\frac{\partial^{2} f}{\partial x_{2} \partial x_{1}}} & {\frac{\partial^{2} f}{\partial x_{2}^{2}}} & {\cdots} & {\frac{\partial^{2} f}{\partial x_{2} \partial x_{n}}} \\ {\vdots} & {\vdots} & {\ddots} & {\vdots} \\ {\frac{\partial^{2} f}{\partial x_{n} \partial x_{1}}} & {\frac{\partial^{2} f}{\partial x_{n} \partial x_{2}}} & {\cdots} & {\frac{\partial^{2} f}{\partial x_{n}^{2}}}\end{array}\right]
A = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ ∂ x 1 2 ∂ 2 f ∂ x 2 ∂ x 1 ∂ 2 f ⋮ ∂ x n ∂ x 1 ∂ 2 f ∂ x 1 ∂ x 2 ∂ 2 f ∂ x 2 2 ∂ 2 f ⋮ ∂ x n ∂ x 2 ∂ 2 f ⋯ ⋯ ⋱ ⋯ ∂ x 1 ∂ x n ∂ 2 f ∂ x 2 ∂ x n ∂ 2 f ⋮ ∂ x n 2 ∂ 2 f ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤
凸函数的性质对研究损失函数的优化问题是有一定帮助的,局部最小值点的区域展现出凸函数的特征(尽管整个函数并不是凸函数)
对于一个集合内的任意两点,如果这两点的连线的所有点都在这个集合内,那么这个集合就是凸集合。
∑
i
α
i
f
(
x
i
)
≥
f
(
∑
i
α
i
x
i
)
and
E
x
[
f
(
x
)
]
≥
f
(
E
x
[
x
]
)
\sum_{i} \alpha_{i} f\left(x_{i}\right) \geq f\left(\sum_{i} \alpha_{i} x_{i}\right) \text { and } E_{x}[f(x)] \geq f\left(E_{x}[x]\right)
i ∑ α i f ( x i ) ≥ f ( i ∑ α i x i ) and E x [ f ( x ) ] ≥ f ( E x [ x ] )
无局部极小值
与凸集的关系
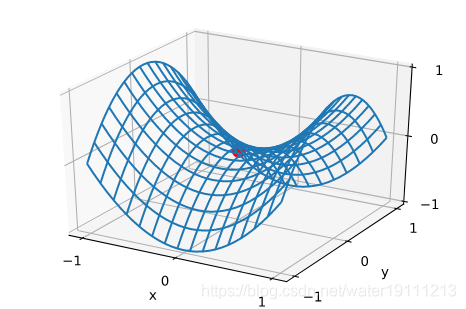
二阶条件
f
′
′
(
x
)
≥
0
⟺
f
(
x
)
f^{''}(x) \ge 0 \Longleftrightarrow f(x)
f ′ ′ ( x ) ≥ 0 ⟺ f ( x )
必要性 (
⇐
\Leftarrow
⇐
对于凸函数:
1
2
f
(
x
+
ϵ
)
+
1
2
f
(
x
−
ϵ
)
≥
f
(
x
+
ϵ
2
+
x
−
ϵ
2
)
=
f
(
x
)
\frac{1}{2} f(x+\epsilon)+\frac{1}{2} f(x-\epsilon) \geq f\left(\frac{x+\epsilon}{2}+\frac{x-\epsilon}{2}\right)=f(x)
2 1 f ( x + ϵ ) + 2 1 f ( x − ϵ ) ≥ f ( 2 x + ϵ + 2 x − ϵ ) = f ( x )
故:
f
′
′
(
x
)
=
lim
ε
→
0
f
(
x
+
ϵ
)
−
f
(
x
)
ϵ
−
f
(
x
)
−
f
(
x
−
ϵ
)
ϵ
ϵ
f^{\prime \prime}(x)=\lim _{\varepsilon \rightarrow 0} \frac{\frac{f(x+\epsilon) - f(x)}{\epsilon}-\frac{f(x) - f(x-\epsilon)}{\epsilon}}{\epsilon}
f ′ ′ ( x ) = ε → 0 lim ϵ ϵ f ( x + ϵ ) − f ( x ) − ϵ f ( x ) − f ( x − ϵ )
f
′
′
(
x
)
=
lim
ε
→
0
f
(
x
+
ϵ
)
+
f
(
x
−
ϵ
)
−
2
f
(
x
)
ϵ
2
≥
0
f^{\prime \prime}(x)=\lim _{\varepsilon \rightarrow 0} \frac{f(x+\epsilon)+f(x-\epsilon)-2 f(x)}{\epsilon^{2}} \geq 0
f ′ ′ ( x ) = ε → 0 lim ϵ 2 f ( x + ϵ ) + f ( x − ϵ ) − 2 f ( x ) ≥ 0
充分性 (
⇒
\Rightarrow
⇒
令
a
<
x
<
b
a < x < b
a < x < b
f
(
x
)
f(x)
f ( x )
f
(
x
)
−
f
(
a
)
=
(
x
−
a
)
f
′
(
α
)
for some
α
∈
[
a
,
x
]
and
f
(
b
)
−
f
(
x
)
=
(
b
−
x
)
f
′
(
β
)
for some
β
∈
[
x
,
b
]
\begin{array}{l}{f(x)-f(a)=(x-a) f^{\prime}(\alpha) \text { for some } \alpha \in[a, x] \text { and }} \\ {f(b)-f(x)=(b-x) f^{\prime}(\beta) \text { for some } \beta \in[x, b]}\end{array}
f ( x ) − f ( a ) = ( x − a ) f ′ ( α ) for some α ∈ [ a , x ] and f ( b ) − f ( x ) = ( b − x ) f ′ ( β ) for some β ∈ [ x , b ]
根据单调性,有
f
′
(
β
)
≥
f
′
(
α
)
f^{\prime}(\beta) \geq f^{\prime}(\alpha)
f ′ ( β ) ≥ f ′ ( α )
f
(
b
)
−
f
(
a
)
=
f
(
b
)
−
f
(
x
)
+
f
(
x
)
−
f
(
a
)
=
(
b
−
x
)
f
′
(
β
)
+
(
x
−
a
)
f
′
(
α
)
≥
(
b
−
a
)
f
′
(
α
)
\begin{aligned} f(b)-f(a) &=f(b)-f(x)+f(x)-f(a) \\ &=(b-x) f^{\prime}(\beta)+(x-a) f^{\prime}(\alpha) \\ & \geq(b-a) f^{\prime}(\alpha) \end{aligned}
f ( b ) − f ( a ) = f ( b ) − f ( x ) + f ( x ) − f ( a ) = ( b − x ) f ′ ( β ) + ( x − a ) f ′ ( α ) ≥ ( b − a ) f ′ ( α )
minimize
x
f
(
x
)
subject to
c
i
(
x
)
≤
0
for all
i
∈
{
1
,
…
,
N
}
\begin{array}{l}{\underset{\mathbf{x}}{\operatorname{minimize}} f(\mathbf{x})} \\ {\text { subject to } c_{i}(\mathbf{x}) \leq 0 \text { for all } i \in\{1, \ldots, N\}}\end{array}
x m i n i m i z e f ( x ) subject to c i ( x ) ≤ 0 for all i ∈ { 1 , … , N }
Boyd & Vandenberghe, 2004
L
(
x
,
α
)
=
f
(
x
)
+
∑
i
α
i
c
i
(
x
)
where
α
i
≥
0
L(\mathbf{x}, \alpha)=f(\mathbf{x})+\sum_{i} \alpha_{i} c_{i}(\mathbf{x}) \text { where } \alpha_{i} \geq 0
L ( x , α ) = f ( x ) + i ∑ α i c i ( x ) where α i ≥ 0
欲使
c
i
(
x
)
≤
0
c_i(x) \leq 0
c i ( x ) ≤ 0
α
i
c
i
(
x
)
\alpha_ic_i(x)
α i c i ( x )
λ
2
∣
∣
w
∣
∣
2
\frac{\lambda}{2} ||w||^2
2 λ ∣ ∣ w ∣ ∣ 2
Proj
X
(
x
)
=
argmin
x
′
∈
X
∥
x
−
x
′
∥
2
\operatorname{Proj}_{X}(\mathbf{x})=\underset{\mathbf{x}^{\prime} \in X}{\operatorname{argmin}}\left\|\mathbf{x}-\mathbf{x}^{\prime}\right\|_{2}
P r o j X ( x ) = x ′ ∈ X a r g m i n ∥ x − x ′ ∥ 2
(Boyd & Vandenberghe, 2004 )
证明:沿梯度反方向移动自变量可以减小函数值
泰勒展开:
f
(
x
+
ϵ
)
=
f
(
x
)
+
ϵ
f
′
(
x
)
+
O
(
ϵ
2
)
f(x+\epsilon)=f(x)+\epsilon f^{\prime}(x)+\mathcal{O}\left(\epsilon^{2}\right)
f ( x + ϵ ) = f ( x ) + ϵ f ′ ( x ) + O ( ϵ 2 )
代入沿梯度方向的移动量
η
f
′
(
x
)
\eta f^{\prime}(x)
η f ′ ( x )
f
(
x
−
η
f
′
(
x
)
)
=
f
(
x
)
−
η
f
′
2
(
x
)
+
O
(
η
2
f
′
2
(
x
)
)
f\left(x-\eta f^{\prime}(x)\right)=f(x)-\eta f^{\prime 2}(x)+\mathcal{O}\left(\eta^{2} f^{\prime 2}(x)\right)
f ( x − η f ′ ( x ) ) = f ( x ) − η f ′ 2 ( x ) + O ( η 2 f ′ 2 ( x ) )
f
(
x
−
η
f
′
(
x
)
)
≲
f
(
x
)
f\left(x-\eta f^{\prime}(x)\right) \lesssim f(x)
f ( x − η f ′ ( x ) ) ≲ f ( x )
x
←
x
−
η
f
′
(
x
)
x \leftarrow x-\eta f^{\prime}(x)
x ← x − η f ′ ( x )
f
(
x
)
=
x
2
f(x) = x^2
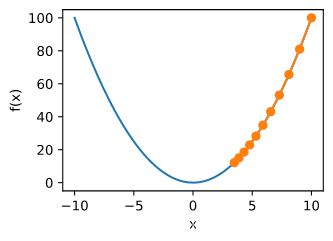
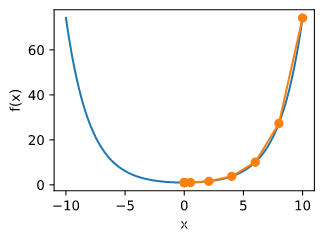
f ( x ) = x 2
def gradf(x):
def gd(eta):
res = gd(0.2)
show_trace(res)
show_trace(gd(0.05))
e.g.
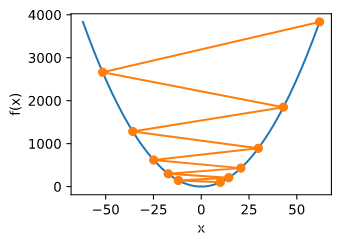
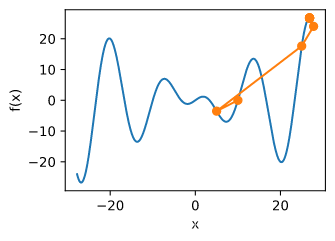
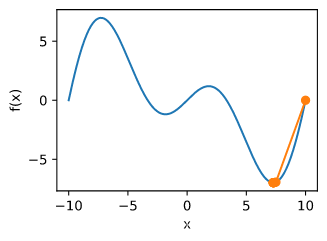
f
(
x
)
=
x
cos
c
x
f(x) = x\cos cx
f ( x ) = x cos c x
c = 0.15 * np.pi
def f(x):
def gradf(x):
show_trace(gd(2)) #学习率过大导致
def show_trace_2d(f, results):
f
(
x
)
=
x
1
2
+
2
x
2
2
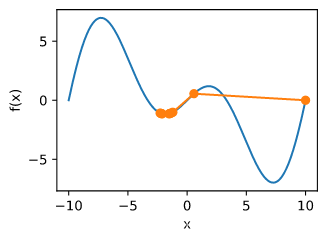
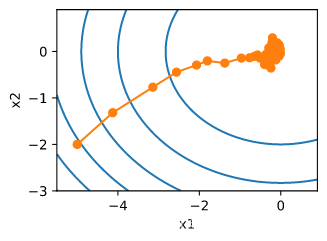
f(x) = x_1^2 + 2x_2^2
f ( x ) = x 1 2 + 2 x 2 2
def f_2d(x1, x2): # 目标函数
def gd_2d(x1, x2):
show_trace_2d(f_2d, train_2d(gd_2d))
(自动调整学习率),实际应用中,由于速度太慢,可能用的少,但可以给我们提供一种思路。
在
x
+
ϵ
x + \epsilon
x + ϵ
f
(
x
+
ϵ
)
=
f
(
x
)
+
ϵ
⊤
∇
f
(
x
)
+
1
2
ϵ
⊤
∇
∇
⊤
f
(
x
)
ϵ
+
O
(
∥
ϵ
∥
3
)
f(\mathbf{x}+\epsilon)=f(\mathbf{x})+\epsilon^{\top} \nabla f(\mathbf{x})+\frac{1}{2} \epsilon^{\top} \nabla \nabla^{\top} f(\mathbf{x}) \epsilon+\mathcal{O}\left(\|\epsilon\|^{3}\right)
f ( x + ϵ ) = f ( x ) + ϵ ⊤ ∇ f ( x ) + 2 1 ϵ ⊤ ∇ ∇ ⊤ f ( x ) ϵ + O ( ∥ ϵ ∥ 3 )
最小值点处满足:
∇
f
(
x
)
=
0
\nabla f(\mathbf{x})=0
∇ f ( x ) = 0
∇
f
(
x
+
ϵ
)
=
0
\nabla f(\mathbf{x} + \epsilon)=0
∇ f ( x + ϵ ) = 0
ϵ
\epsilon
ϵ
∇
f
(
x
)
+
H
f
ϵ
=
0
and hence
ϵ
=
−
H
f
−
1
∇
f
(
x
)
\nabla f(\mathbf{x})+\boldsymbol{H}_{f} \boldsymbol{\epsilon}=0 \text { and hence } \epsilon=-\boldsymbol{H}_{f}^{-1} \nabla f(\mathbf{x})
∇ f ( x ) + H f ϵ = 0 and hence ϵ = − H f − 1 ∇ f ( x )
def f(x):
def gradf(x):
def hessf(x):
def newton(eta=1):
show_trace(newton())
c = 0.15 * np.pi
def f(x):
def gradf(x):
def hessf(x):
show_trace(newton()) #错误,默认学习率1
show_trace(newton(0.5))
只考虑在函数为凸函数 , 且最小值点上
f
′
′
(
x
∗
)
>
0
f''(x^*) > 0
f ′ ′ ( x ∗ ) > 0
令
x
k
x_k
x k
k
k
k
x
x
x
e
k
:
=
x
k
−
x
∗
e_{k}:=x_{k}-x^{*}
e k : = x k − x ∗
x
k
x_k
x k
x
∗
x^{*}
x ∗
f
′
(
x
∗
)
=
0
f'(x^{*}) = 0
f ′ ( x ∗ ) = 0
0
=
f
′
(
x
k
−
e
k
)
=
f
′
(
x
k
)
−
e
k
f
′
′
(
x
k
)
+
1
2
e
k
2
f
′
′
′
(
ξ
k
)
for some
ξ
k
∈
[
x
k
−
e
k
,
x
k
]
0=f^{\prime}\left(x_{k}-e_{k}\right)=f^{\prime}\left(x_{k}\right)-e_{k} f^{\prime \prime}\left(x_{k}\right)+\frac{1}{2} e_{k}^{2} f^{\prime \prime \prime}\left(\xi_{k}\right) \text{for some } \xi_{k} \in\left[x_{k}-e_{k}, x_{k}\right]
0 = f ′ ( x k − e k ) = f ′ ( x k ) − e k f ′ ′ ( x k ) + 2 1 e k 2 f ′ ′ ′ ( ξ k ) for some ξ k ∈ [ x k − e k , x k ]
两边除以
f
′
′
(
x
k
)
f''(x_k)
f ′ ′ ( x k )
e
k
−
f
′
(
x
k
)
/
f
′
′
(
x
k
)
=
1
2
e
k
2
f
′
′
′
(
ξ
k
)
/
f
′
′
(
x
k
)
e_{k}-f^{\prime}\left(x_{k}\right) / f^{\prime \prime}\left(x_{k}\right)=\frac{1}{2} e_{k}^{2} f^{\prime \prime \prime}\left(\xi_{k}\right) / f^{\prime \prime}\left(x_{k}\right)
e k − f ′ ( x k ) / f ′ ′ ( x k ) = 2 1 e k 2 f ′ ′ ′ ( ξ k ) / f ′ ′ ( x k )
代入更新方程
x
k
+
1
=
x
k
−
f
′
(
x
k
)
/
f
′
′
(
x
k
)
x_{k+1} = x_{k} - f^{\prime}\left(x_{k}\right) / f^{\prime \prime}\left(x_{k}\right)
x k + 1 = x k − f ′ ( x k ) / f ′ ′ ( x k )
x
k
−
x
∗
−
f
′
(
x
k
)
/
f
′
′
(
x
k
)
=
1
2
e
k
2
f
′
′
′
(
ξ
k
)
/
f
′
′
(
x
k
)
x_k - x^{*} - f^{\prime}\left(x_{k}\right) / f^{\prime \prime}\left(x_{k}\right) =\frac{1}{2} e_{k}^{2} f^{\prime \prime \prime}\left(\xi_{k}\right) / f^{\prime \prime}\left(x_{k}\right)
x k − x ∗ − f ′ ( x k ) / f ′ ′ ( x k ) = 2 1 e k 2 f ′ ′ ′ ( ξ k ) / f ′ ′ ( x k )
x
k
+
1
−
x
∗
=
e
k
+
1
=
1
2
e
k
2
f
′
′
′
(
ξ
k
)
/
f
′
′
(
x
k
)
x_{k+1} - x^{*} = e_{k+1} = \frac{1}{2} e_{k}^{2} f^{\prime \prime \prime}\left(\xi_{k}\right) / f^{\prime \prime}\left(x_{k}\right)
x k + 1 − x ∗ = e k + 1 = 2 1 e k 2 f ′ ′ ′ ( ξ k ) / f ′ ′ ( x k )
当
1
2
f
′
′
′
(
ξ
k
)
/
f
′
′
(
x
k
)
≤
c
\frac{1}{2} f^{\prime \prime \prime}\left(\xi_{k}\right) / f^{\prime \prime}\left(x_{k}\right) \leq c
2 1 f ′ ′ ′ ( ξ k ) / f ′ ′ ( x k ) ≤ c
e
k
+
1
≤
c
e
k
2
e_{k+1} \leq c e_{k}^{2}
e k + 1 ≤ c e k 2
x
←
x
−
η
diag
(
H
f
)
−
1
∇
x
\mathbf{x} \leftarrow \mathbf{x}-\eta \operatorname{diag}\left(H_{f}\right)^{-1} \nabla \mathbf{x}
x ← x − η d i a g ( H f ) − 1 ∇ x
对于有
n
n
n
f
i
(
x
)
f_i(x)
f i ( x )
i
i
i
f
(
x
)
=
1
n
∑
i
=
1
n
f
i
(
x
)
f(\mathbf{x})=\frac{1}{n} \sum_{i=1}^{n} f_{i}(\mathbf{x})
f ( x ) = n 1 i = 1 ∑ n f i ( x )
其梯度为:
∇
f
(
x
)
=
1
n
∑
i
=
1
n
∇
f
i
(
x
)
\nabla f(\mathbf{x})=\frac{1}{n} \sum_{i=1}^{n} \nabla f_{i}(\mathbf{x})
∇ f ( x ) = n 1 i = 1 ∑ n ∇ f i ( x )
使用该梯度的一次更新的时间复杂度为
O
(
n
)
\mathcal{O}(n)
O ( n )
随机梯度下降更新公式
O
(
1
)
\mathcal{O}(1)
O ( 1 )
x
←
x
−
η
∇
f
i
(
x
)
\mathbf{x} \leftarrow \mathbf{x}-\eta \nabla f_{i}(\mathbf{x})
x ← x − η ∇ f i ( x )
且有:
E
i
∇
f
i
(
x
)
=
1
n
∑
i
=
1
n
∇
f
i
(
x
)
=
∇
f
(
x
)
\mathbb{E}_{i} \nabla f_{i}(\mathbf{x})=\frac{1}{n} \sum_{i=1}^{n} \nabla f_{i}(\mathbf{x})=\nabla f(\mathbf{x})
E i ∇ f i ( x ) = n 1 i = 1 ∑ n ∇ f i ( x ) = ∇ f ( x )
f
(
x
1
,
x
2
)
=
x
1
2
+
2
x
2
2
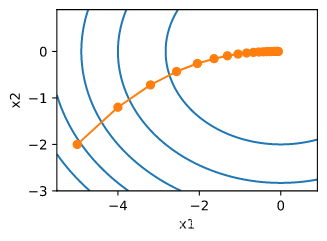
f(x_1, x_2) = x_1^2 + 2 x_2^2
f ( x 1 , x 2 ) = x 1 2 + 2 x 2 2
def gradf(x1, x2):
def sgd(x1, x2): # Simulate noisy gradient
eta = 0.1
规划学习率
η
(
t
)
=
η
i
if
t
i
≤
t
≤
t
i
+
1
piecewise constant
η
(
t
)
=
η
0
⋅
e
−
λ
t
exponential
η
(
t
)
=
η
0
⋅
(
β
t
+
1
)
−
α
polynomial
\begin{array}{ll}{\eta(t)=\eta_{i} \text { if } t_{i} \leq t \leq t_{i+1}} & {\text { piecewise constant }} \\ {\eta(t)=\eta_{0} \cdot e^{-\lambda t}} & {\text { exponential }} \\ {\eta(t)=\eta_{0} \cdot(\beta t+1)^{-\alpha}} & {\text { polynomial }}\end{array}
η ( t ) = η i if t i ≤ t ≤ t i + 1 η ( t ) = η 0 ⋅ e − λ t η ( t ) = η 0 ⋅ ( β t + 1 ) − α piecewise constant exponential polynomial
ctr = 1
ctr = 1
梯度下降和随机梯度下降折中的一种方法。
features, labels = get_data_ch7()
import pandas as pd
def sgd(params, states, hyperparams): #params,模型参数;states,不用;hyperparams,学习率
def train_ch7(optimizer_fn, states, hyperparams, features, labels,
w = torch.nn.Parameter(torch.tensor(np.random.normal(0, 0.01, size=(features.shape[1], 1)), dtype=torch.float32),
requires_grad=True) #weight
b = torch.nn.Parameter(torch.zeros(1, dtype=torch.float32), requires_grad=True)
def eval_loss():
return loss(net(features, w, b), labels).mean().item()
ls = [eval_loss()]
data_iter = torch.utils.data.DataLoader(
torch.utils.data.TensorDataset(features, labels), batch_size, shuffle=True)
for _ in range(num_epochs):
start = time.time()
for batch_i, (X, y) in enumerate(data_iter):
l = loss(net(X, w, b), y).mean() # 使用平均损失
# 梯度清零
if w.grad is not None:
w.grad.data.zero_()
b.grad.data.zero_()
l.backward()
optimizer_fn([w, b], states, hyperparams) # 迭代模型参数
if (batch_i + 1) * batch_size % 100 == 0:
ls.append(eval_loss()) # 每100个样本记录下当前训练误差
# 打印结果和作图
print('loss: %f, %f sec per epoch' % (ls[-1], time.time() - start))
d2l.set_figsize()
d2l.plt.plot(np.linspace(0, num_epochs, len(ls)), ls)
d2l.plt.xlabel('epoch')
d2l.plt.ylabel('loss')
def train_sgd(lr, batch_size, num_epochs=2):
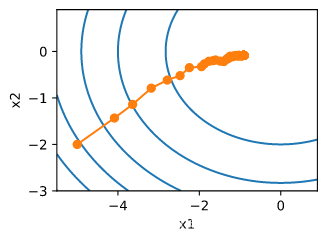
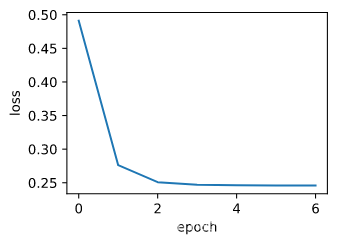
train_sgd(1, 1500, 6)
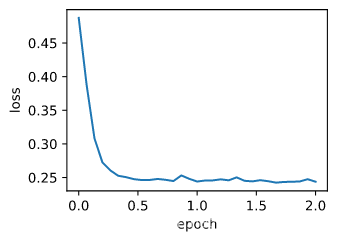
train_sgd(0.005, 1)
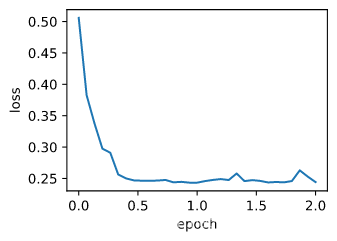
train_sgd(0.05, 10)