Indirect Kalman Filter for 3D Attitude Estimation

翻译一篇2005的论文。

1 四元数代数中的元素

1.1 四元数定义

四元数通常定义为

q ⃗ = q 4 + q 1 i + q 2 j + q 3 k

$\vec{q}=q_4+q_1i+q_2j+q_3k$
其中 i，j，k是纯虚数，满足以下条件

i 2 = - 1, j 2 = - 1, k 2 = - 1 - i j = j i = k, - j k = k j = i, - k i = i k = j

$i^2=-1,j^2=-1,k^2=-1\\ -ij=ji=k,-jk=kj=i,-ki=ik=j$
数字

q4 $q_4$ 是一个实数或者说四元数的标量部分，

q1i+q2j+q3k $q_1i+q_2j+q_3k$ 是虚部或者说是四元数的矢量部分，寺院数量可以被写为4维的列矩阵，

q ⃗ = [q q 4] = [q 1 q 2 q 3 q 4] T

$\vec{q}=\begin{bmatrix} \large q \\ q_4 \end{bmatrix}=\begin{bmatrix} q_1 & q_2 & q_3 & q_4 \end{bmatrix}^T$

如果数 $\large q$ 和 $q_4$ 满足

q = ⎡ ⎣ ⎢ k x s i n (θ / 2) k y s i n (θ / 2) k z s i n (θ / 2) ⎤ ⎦ ⎥ = k ⃗ s i n (θ / 2), q 4 = c o s (θ / 2)

$\large q=\begin{bmatrix} k_xsin(\theta/2) \\ k_ysin(\theta/2) \\ k_zsin(\theta/2)\end{bmatrix}=\vec{k}sin(\theta/2),q 4 = cos(θ/2)$
那么元素

q1,...,q4 $q_1 , . . . , q_4$ 叫做“旋转四元数”或者“欧拉对称参数”，在这个等式中，

k⃗ $\vec{k}$ 是轴向的单位四元数，

θ $θ$ 是旋转角度，旋转四元数是一个单位四元数，满足

| q ⃗ | = q ⃗ T q ⃗ - - - \sqrt = | q | 2 + q 24 - - - - - - - - \sqrt = 1

$|\vec{q}|=\sqrt{\vec{q}^T\vec{q}}=\sqrt{|\large q|^2+q_4^2}=1$
因此我们用术语四元数来表示旋转四元数。

1.2 四元数乘法

四元数乘法定义为

q ̄ \otimes p ̄ = (q 4 + q 1 i + q 2 j + q 3 k) (p 4 + p 1 i + p 2 j + p 3 k) = q 4 p 4 - q 1 p 1 - q 2 p 2 - q 3 p 3 + (q 4 p 1 + q 1 p 4 - q 2 p 3 + q 3 p 2) i + (q 4 p 2 + q 2 p 4 - q 3 p 1 + q 1 p 3) j + (q 4 p 3 + q 3 p 4 - q 1 p 2 + q 2 p 1) k = ⎡ ⎣ ⎢ ⎢ ⎢ ⎢ q 4 p 1 + q 3 p 2 - q 2 p 3 + q 1 p 4 - q 3 p 1 + q 4 p 2 + q 1 p 3 + q 2 p 4 q 2 p 1 - q 1 p 2 + q 4 p 3 + q 3 p 4 - q 1 p 1 - q 2 p 2 - q 2 p 3 + q 4 p 4 ⎤ ⎦ ⎥ ⎥ ⎥ ⎥

$q̄ ⊗ p̄ =(q 4 + q 1 i + q 2 j + q 3 k) (p 4 + p 1 i + p 2 j + p 3 k)\\ =q 4 p 4 − q 1 p 1 − q 2 p 2 − q 3 p 3 + (q 4 p 1 + q 1 p 4 − q 2 p 3 + q 3 p 2 ) i\\+ (q 4 p 2 + q 2 p 4 − q 3 p 1 + q 1 p 3 ) j + (q 4 p 3 + q 3 p 4 − q 1 p 2 + q 2 p 1 ) k\\=\begin{bmatrix} q_4p_1+q_3p_2-q_2p_3+q_1p_4 \\ -q_3p_1+q_4p_2+q_1p_3+q_2p_4 \\ q_2p_1-q_1p_2+q_4p_3+q_3p_4 \\ -q_1p_1-q_2p_2-q_2p_3+q_4p_4 \end{bmatrix}$ 四元数乘法可以另写成矩阵形式，为此，我们先介绍矩阵叉乘符号，使用反对称运算

⌊ q \times ⌋ = ⎡ ⎣ ⎢ 0 q 3 - q 2 - q 3 0 q 1 q 2 - q 1 0 ⎤ ⎦ ⎥

$\lfloor q× \rfloor=\begin{bmatrix} 0 & -q_3 & q_2\\ q_3 & 0 & -q_1 \\ -q_2 & q_1 & 0\end{bmatrix}$ 叉乘可以被写成

q \times p = ∣ ∣ ∣ ∣ i q 1 p 1 j q 2 p 2 k q 3 p 3 ∣ ∣ ∣ ∣ = ⎡ ⎣ ⎢ q 2 p 3 - q 3 p 2 q 3 p 1 - q 1 p 3 q 1 p 2 - q 2 p 1 ⎤ ⎦ ⎥ = ⎡ ⎣ ⎢ 0 q 3 - q 2 - q 3 0 q 1 q 2 - q 1 0 ⎤ ⎦ ⎥ ⎡ ⎣ ⎢ p 1 p 2 p 3 ⎤ ⎦ ⎥ = ⌊ q \times ⌋ p

$\large q \small × \large p \small = \\\begin{vmatrix} i & j & k \\ q_1 & q_2 & q_3 \\ p_1 & p_2 & p_3 \\ \end{vmatrix} = \begin{bmatrix} q_2p_3-q_3p_2\\ q_3p_1-q_1p_3 \\ q_1p_2-q_2p_1\end{bmatrix}=\begin{bmatrix} 0 & -q_3 & q_2\\ q_3 & 0 & -q_1 \\ -q_2 & q_1 & 0\end{bmatrix}\begin{bmatrix} p_1\\ p_2\\ p_3\end{bmatrix}=\lfloor q× \rfloor\large p$ 四元数的乘法可以被重写成

q ̄ \otimes p ̄ = L (q ̄) p ̄ = ⎡ ⎣ ⎢ ⎢ ⎢ ⎢ q 4 - q 3 q 2 - q 1 q 3 q 4 - q 1 - q 2 - q 2 q 1 q 4 - q 3 q 1 q 2 q 3 q 4 ⎤ ⎦ ⎥ ⎥ ⎥ ⎥ ⎡ ⎣ ⎢ ⎢ ⎢ ⎢ p 1 p 2 p 3 p 4 ⎤ ⎦ ⎥ ⎥ ⎥ ⎥ = [q 4 I 3 \times 3 - ⌊ q \times ⌋ - q T q q 4] [p p 4] = [q 4 p + p 4 q - q \times p p 4 q 4 - q T p] = [p 4 q + q 4 p + ⌊ p \times ⌋ q p 4 q 4 - p T q] = [p 4 I 3 \times 3 + ⌊ p \times ⌋ - p T p p 4] [q q 4] = ⎡ ⎣ ⎢ ⎢ ⎢ ⎢ p 4 p 3 - p 2 - p 1 - p 3 p 4 p 1 - p 2 p 2 - p 1 p 4 - p 3 p 1 p 2 p 3 p 4 ⎤ ⎦ ⎥ ⎥ ⎥ ⎥ ⎡ ⎣ ⎢ ⎢ ⎢ ⎢ q 1 q 2 q 3 q 4 ⎤ ⎦ ⎥ ⎥ ⎥ ⎥ = R (p ̄) q ̄

$q̄ ⊗ p̄ = \cal L(q̄)p̄ \\ = \begin{bmatrix} q_4 & q_3 & -q_2 & q_1\\ -q_3 & q_4 & q_1 & q_2 \\ q_2 & -q_1 & q_4 & q_3 \\ -q_1 & -q_2 & -q_3 & q_4\end{bmatrix}\begin{bmatrix} p_1\\ p_2 \\ p_3 \\ p_4\end{bmatrix}\\ =\begin{bmatrix} q_4 \large I_{3×3}-\lfloor q× \rfloor & \large q\\-\large q^T & q_4\end{bmatrix} \begin{bmatrix} \large p \\ p_4 \end{bmatrix}\\ = \begin{bmatrix} q_4\large p+\small p_4\large q - \large q \small × \large p \\ p_4q_4 - \large q^Tp \end{bmatrix}\\ =\begin{bmatrix} p_4\large q+\small q_4\large p + \lfloor p× \rfloor \large q \\ p_4q_4 - \large p^Tq \end{bmatrix}\\ =\begin{bmatrix} p_4 \large I_{3×3}+\lfloor p× \rfloor & \large p\\-\large p^T & p_4\end{bmatrix} \begin{bmatrix} \large q \\ q_4 \end{bmatrix}\\ =\begin{bmatrix} p_4 & -p_3 & p_2 & p_1\\ p_3 & p_4 & -p_1 & p_2 \\ -p_2 & p_1 & p_4 & p_3 \\ -p_1 & -p_2 & -p_3 & p_4\end{bmatrix}\begin{bmatrix} q_1\\ q_2 \\ q_3 \\ q_4\end{bmatrix}\\ =\cal R(p̄)q̄$

L $\cal L$ 和

R $\cal R$ 的属性如下：

L (q ̄ - 1) = L T (q ̄) R (p ̄ - 1) = R T (p ̄) L = [Ψ (q ̄) q ̄] R = [Ξ (p ̄) p ̄]

$\cal L(q̄^{-1})=\cal L^T(q̄)\\ \cal R(p̄^{-1})=\cal R^T(p̄)\\ \cal L=\begin{bmatrix} Ψ(q̄) & q̄\end{bmatrix}\\ \cal R=\begin{bmatrix} Ξ(p̄) & p̄\end{bmatrix}$
其中Ψ和Ξ定义为

Ψ = [q 4 I 3 \times 3 - ⌊ q \times ⌋ - q T] Ξ = [p 4 I 3 \times 3 - ⌊ p \times ⌋ - p T]

$Ψ = \begin{bmatrix} q_4 \large I_{3×3}-\lfloor q× \rfloor \\ -\large q^T\end{bmatrix}\\ Ξ = \begin{bmatrix} p_4 \large I_{3×3}-\lfloor p× \rfloor \\ -\large p^T\end{bmatrix}$
如果两个旋转，

CA $C_A$ and

CB $C_B$ 是相关的，例如

CACX=CXCB $C_A C_X = C_X C_B$ (手眼标定),那么相关的矩阵

L(q̄ A)−R(q̄ B) $\cal L(q̄ A)-R(q̄ B)$ 是反对称矩阵，秩为2，特别，

q̄ A4=q̄ B4 $q̄ A_4 = q̄ B_4$ ,

||qA||=||qB|| $||q A || = ||q B ||$ 。
四元数有一个关于乘法中性的元素，定义为

q ̄ 0 = [0001] T q ̄ \otimes q ̄ 0 = q ̄ 0 \otimes q ̄ = q ̄

$q̄_0= \begin{bmatrix} 0 & 0 & 0 & 1\end{bmatrix}^T\\ q̄⊗ q̄_0 = q̄_0 ⊗ q̄ = q̄$
旋转的逆描述为逆或者负数共扼四元数，表示为

q ̄ - 1 = [- q q 4] = [- k s i n (θ / 2) c o s (θ / 2)] = [k s i n (- θ / 2) c o s (- θ / 2)]

$q̄^{-1}=\begin{bmatrix} -\large q \\ q_4\end{bmatrix} = \begin{bmatrix} -\large k \small sin(θ/2) \\ cos(θ/2)\end{bmatrix} = \begin{bmatrix} \large k \small sin(-θ/2) \\ cos(-θ/2)\end{bmatrix}$

q ̄ \otimes q ̄ - 1 = q ̄ - 1 \otimes q ̄ = q ̄ 0 (q ̄ \otimes p ̄) - 1 = p ̄ - 1 \otimes q ̄ - 1

$q̄ ⊗ q̄^{−1} = q̄^{−1} ⊗ q̄ = q̄ 0\\(q̄ ⊗ p̄)^{−1} = p̄^{−1} ⊗ q̄^{−1}$

1.3 有用的性质

1.3.1 叉乘反对称矩阵 $\lfloor \omega\times \rfloor$ 的属性

反交換律

⌊ ω \times ⌋ = - ⌊ ω \times ⌋ T

$\lfloor \omega\times \rfloor = -\lfloor \omega\times \rfloor ^T$

⌊ a \times ⌋ b = - ⌊ b \times ⌋ a ⟸ a T ⌊ b \times ⌋ = - b T ⌊ a \times ⌋

$\large\lfloor \large a \small\times \large\rfloor \large b \small= -\large\lfloor \large b \small\times \large\rfloor \large a \\\impliedby \large a^T \lfloor\large b \small\times \large\rfloor \small= -\large b^T\lfloor \large a \small\times \large\rfloor$
加法分配律

⌊ a \times ⌋ + ⌊ b \times ⌋ = ⌊ a + b \times ⌋

$\lfloor \large a \small\times \rfloor + \lfloor \large b \small\times \rfloor= \lfloor \large a \small + \large b \small\times \rfloor$
标量乘法

c \cdot ⌊ ω \times ⌋ = ⌊ c \cdot ω \times ⌋

$c\cdot\lfloor \omega\times \rfloor = \lfloor c\cdot \omega\times \rfloor$
平行矢量叉乘

ω \times (c \cdot ω) = c \cdot ⌊ ω \times ⌋ ω = - c \cdot (ω T ⌊ ω \times ⌋) T = 0 3 \times 1

${\large ω} × (c · {\large ω}) = c · \lfloor{\large ω} ×\rfloor {\large ω} \\ =−c · ({\large ω}^T\lfloor {\large ω} ×\rfloor )^T= 0_{3×1}$
拉格朗日公式

⌊ a \times ⌋ ⌊ b \times ⌋ = b a T - (a T b) I 3 \times 3 ⟸ a \times (b \times c) = b (a T c) - c (a T b)

$\lfloor {\large a}\times \rfloor \lfloor {\large b}\times \rfloor = {\large b}{\large a}^T-({\large a}^T{\large b}){\large I_{3×3}}\\ \impliedby {\large a} ×({\large b}×{\large c}) = {\large b}({\large a}^T{\large c})-{\large c}({\large a}^T{\large b})$

⌊ a \times ⌋ ⌊ b \times ⌋ + a b T = ⌊ b \times ⌋ ⌊ a \times ⌋ + b a T ⌊ (a \times b) \times ⌋ = b a T - a b T

$\lfloor {\large a}\times \rfloor \lfloor {\large b}\times \rfloor + {\large a}{\large b}^T= \lfloor {\large b}\times \rfloor \lfloor {\large a}\times \rfloor + {\large b}{\large a}^T\\ \lfloor ({\large a} ×{\large b} )\times \rfloor = {\large b}{\large a}^T-{\large a}{\large b}^T$
雅可比恒等式

⌊ a \times ⌋ ⌊ b \times ⌋ c + ⌊ b \times ⌋ ⌊ c \times ⌋ a + ⌊ c \times ⌋ ⌊ a \times ⌋ b = 0

$\lfloor {\large a}\times \rfloor \lfloor {\large b}\times \rfloor{\large c}+\lfloor {\large b}\times \rfloor \lfloor {\large c}\times \rfloor{\large a} +\lfloor {\large c}\times \rfloor \lfloor {\large a}\times \rfloor{\large b}= 0$
旋转

⌊ C a \times ⌋ = C ⌊ a \times ⌋ C T C (a \times b) = (C a) \times (C b)

$\lfloor {\large C}{\large a}\times\rfloor = {\large C}\lfloor {\large a} \times \rfloor {\large C}^T \\ {\large C}({\large a}\times{\large b}) = ({\large C}{\large a})\times({\large C}{\large b})$

四元数表示的向量叉乘，如果我们定义四元数

ā = [a 0], b ̄ = [b 0], c ̄ = [c 0] = [a \times b 0]

$ā = \begin{bmatrix}{\large a}\\ 0\end{bmatrix},b̄ = \begin{bmatrix}{\large b}\\ 0\end{bmatrix},c̄ = \begin{bmatrix}{\large c}\\ 0\end{bmatrix} = \begin{bmatrix}{\large a}\times{\large b}\\ 0\end{bmatrix}$
我们可以得到：

c ̄ = 1 2 (b ̄ \otimes ā + ā \otimes b ̄ - 1) = 1 2 ((L (b) + R T (b)) ā = 1 2 ([- 2 ⌊ b \times ⌋ 0 00] [a 0])

$c̄ = \frac{1}{2}( b̄ ⊗ ā + ā ⊗ b̄^{-1})\\ = \frac{1}{2}((\cal L(b)+\cal R^T(b))ā\\ = \frac{1}{2}(\begin{bmatrix}-2\lfloor {\large b}\times\rfloor & 0\\ 0 & 0\end{bmatrix}\begin{bmatrix} {\large a} \\ 0 \end{bmatrix})$

$\lfloor {\large\omega}\times \rfloor$ 的次方

⌊ ω \times ⌋ 2 = ω ω T - | ω | 2 \cdot I 3 \times 3 ⌊ ω \times ⌋ 3 = - | ω | 2 \cdot ⌊ ω \times ⌋ ⌊ ω \times ⌋ 4 = - | ω | 2 \cdot ⌊ ω \times ⌋ 2 ⌊ ω \times ⌋ 5 = | ω | 4 \cdot ⌊ ω \times ⌋

$\lfloor {\large\omega}\times \rfloor^2 = {\large\omega}{\large\omega}^T-|{\large\omega}|^2\cdot{\large I}_{3\times3} \\ \lfloor {\large\omega}\times \rfloor^3 = -|{\large\omega}|^2\cdot\lfloor {\large\omega}\times \rfloor\\ \lfloor {\large\omega}\times \rfloor^4 = -|{\large\omega}|^2\cdot\lfloor {\large\omega}\times \rfloor^2\\ \lfloor {\large\omega}\times \rfloor^5 = |{\large\omega}|^4\cdot\lfloor {\large\omega}\times \rfloor$
以此类推。

1.3.2 Ω矩阵的性质

矩阵Ω在一个向量和四元数相乘时出现，他用于例如四元数微分，具有如下属性：

Ω (ω) = ⎡ ⎣ ⎢ ⎢ ⎢ ⎢ 0 - ω z ω y - ω x ω z 0 - ω x - ω y - ω y ω x 0 ω z ω x ω y ω z 0 ⎤ ⎦ ⎥ ⎥ ⎥ ⎥ = [- ⌊ ω \times ⌋ - ω T ω 0]

$Ω(ω) = \begin{bmatrix} 0 & ω_z & -ω_y & ω_x \\ -ω_z & 0 & ω_x & ω_y \\ ω_y & -ω_x & 0 & ω_z \\ -ω_x & -ω_y & ω_z & 0\end{bmatrix}\\ = \begin{bmatrix}-\lfloor ω\times\rfloor & ω\\ -ω^T & 0\end{bmatrix}$

Ω (ω) 2 = [⌊ ω \times ⌋ 2 - ω ω T - ω T ⌊ ω \times ⌋ - ⌊ ω \times ⌋ ω - ω T ω] = [- | ω | 2 \cdot I 3 \times 3 - 0 1 \times 3 0 3 \times 1 - | ω | 2] = - | ω | 2 \cdot I 4 \times 4

$Ω(ω)^2 = \begin{bmatrix}\lfloor ω\times\rfloor^2-ωω^T & -\lfloor ω\times\rfloorω\\ -ω^T\lfloor ω\times\rfloor & −ω^T ω\end{bmatrix}\\ =\begin{bmatrix}-|ω|^2\cdot{\large I_{3\times3}} & 0_{3\times1}\\ -0_{1\times3}& −|ω|^2 \end{bmatrix}\\ =−|ω|^2 · I_{4×4}$

Ω (ω) 3 = - | ω | 2 \cdot Ω (ω)

$Ω(ω)^3 = −|ω|^2· Ω(ω)$

Ω (ω) 4 = - | ω | 4 \cdot I 4 \times 4

$Ω(ω)^4 = −|ω|^4· I_{4\times4}$

Ω (ω) 5 = | ω | 4 \cdot Ω (ω)

$Ω(ω)^5 = |ω|^4· Ω(ω)$

Ω (ω) 6 = - | ω | 6 \cdot I 4 \times 4

$Ω(ω)^6 = −|ω|^6· I_{4\times4}$
以此类推。

1.3.3 Ξ矩阵的性质

Ξ(q̄)矩阵在一个向量与四元数相乘时出现。Ξ(q̄) 和 Ω(a)的关系，与乘法矩阵 $L(q̄)$ 和 $R(p̄)$ 的关系相同。

Ξ (q ̄) = ⎡ ⎣ ⎢ ⎢ ⎢ ⎢ q 4 q 3 - q 2 - q 1 - q 3 q 4 q 1 - q 2 q 2 - q 1 q 4 - q 3 ⎤ ⎦ ⎥ ⎥ ⎥ ⎥ = [q 4 \cdot I 3 \times 3 + ⌊ q \times ⌋ - q T]

$Ξ(q̄) = \begin{bmatrix} q_4 & -q_3 & q_2 \\ q_3 & q_4 & -q_1 \\ -q_2 & q_1 & q_4 \\ -q_1 & -q_2 & -q_3 \end{bmatrix}=\begin{bmatrix} q_4 \cdot {\large I_{3\times3}}+\lfloor {\large q}\times \rfloor\\ -{\large q}^T \end{bmatrix}$

Ξ T (q ̄) = ⎡ ⎣ ⎢ q 4 - q 3 q 2 q 3 q 4 - q 1 - q 2 q 1 q 4 - q 1 - q 2 - q 3 ⎤ ⎦ ⎥

$Ξ^T(q̄) = \begin{bmatrix} q_4 & q_3 & -q_2 & -q_1\\ -q_3 & q_4 & q_1 & -q_2\\ q_2 & -q_1 & q_4 & -q_3\end{bmatrix}$
可以看出

Ξ T (q ̄) Ξ (q ̄) = I 3 \times 3 Ξ (q ̄) Ξ T (q ̄) = I 4 \times 4 - q ̄ q ̄ T Ξ T (q ̄) q ̄ = 0 3 \times 1

$Ξ^T (q̄)Ξ(q̄) = I_{3×3}\\ Ξ (q̄)Ξ^T(q̄) = I_{4×4}-q̄ q̄^T\\ Ξ T (q̄)q̄ = 0_{3\times1}$
Ξ 和 Ω的关系

Ω (a) q ̄ = Ξ (q ̄) a

$Ω(a)q̄ = Ξ(q̄)a$

1.4 四元数和旋转矩阵之间的关系

给定一个向量P，我们定义对应的四元数为

p ̄ = [p 0]

$p̄ = \begin{bmatrix} {\large p}\\0\end{bmatrix}$ 我们将利用在不同坐标系中表示的向量之间的两个关系

p L p = C (q ̄) L G C (q ̄) p G p

$\sideset{^L}{}{\large p }= \sideset{^L_G}{}{\large C(q̄)} \sideset{^G}{}{\large p}$

q̄ =̄ LḠ q $q̄ = \sideset{^L_G}q̄$ 和

CLGC(q̄ ) $\sideset{^L_G}{}C(q̄)$ 是3×3的旋转矩阵，是(全局)坐标系{G}相对于(局部)坐标系{L}。
也可以将一个向量从一个坐标系转移到另一个坐标系通过将四元数分别左乘和右乘旋转四元数和它的逆。

p L p = q L G q ̄ \otimes p ̄ G p ̄ \otimes q L G q - 1 ̄ = [(2 q 24 - 1) I 3 \times 3 - 2 q 4 ⌊ q \times ⌋ + 2 q q T 0] [P G P 0]

$\sideset{^L}{}{\large p} = \sideset{^L_G}{}q̄⊗ \sideset{^G}{}{\large p̄ }⊗\sideset{^L_G}{^{-1}}q̄\\ =\begin{bmatrix} (2q_4^2-1){\large I_{3\times3}-2q_4\lfloor{\large q}\times\rfloor+2{\large q}{\large q}^T} \\ 0\end{bmatrix}\begin{bmatrix} \sideset{^G}{}{\large P} \\ 0\end{bmatrix}$
由此我们得到四元数和他对应的旋转矩阵之间的关系。

C L G C (q ̄) = (2 q 4 - 1) I 3 \times 3 - 2 q 4 ⌊ q \times ⌋ + 2 q q T

$\sideset{^L_G}{}C(q̄) = (2q_4 − 1){\large I _{3×3 }}− 2q_4 \lfloor q ×\rfloor + 2qq^T$
也可以写成

C L G C (q ̄) = Ξ T (q ̄) Ψ (q ̄)

$\sideset{^L_G}{}C(q̄) = Ξ^T (q̄)Ψ(q̄)$
我们可以通过三个四元数相乘得到相似的形式，尽管这没有什么物理意义

q ̄ \otimes p ̄ \otimes q ̄ - 1 = L (q ̄) R T (q ̄) p ̄ = [C (q ̄) 0 01] [p p 4] = [C (q ̄) p p 4]

$q̄ ⊗ p̄ ⊗ q̄^{−1}\\ = \cal L(q̄)R^T(q̄)p̄\\ =\begin{bmatrix}{\large C(q̄)} & 0\\ 0 & 1\end{bmatrix}\begin{bmatrix} {\large p}\\ p_4\end{bmatrix}\\ = \begin{bmatrix}{\large C(q̄)}{\large p} \\ p_4\end{bmatrix}$
如果只有一个很小的旋转

δq̄ $δ q̄$ ,我们可以用小的角度近似值来简化上面的表达式。我们可以描述一个小角度四元数

δ q ̄ = [δ q δ q 4] = [k s i n (δ θ / 2) c o s (δ θ / 2)] \approx [δ θ / 2 1]

$δq̄ = \begin{bmatrix} δ{\large q}\\ δq_4\end{bmatrix}\\ = \begin{bmatrix}{\large k}sin(δθ/2)\\cos(δθ/2)\end{bmatrix}\\ \approx \begin{bmatrix}δθ/2\\1\end{bmatrix}$
我们得到对应的旋转矩阵表达式

C L G C (δ q ̄) \approx I 3 \times 3 - ⌊ δ θ \times ⌋

$\sideset{^L_G}{}C(δq̄) \approx I_{3\times3}-\lfloor δθ × \rfloor$

旋转矩阵也可以用轴角表示

C L G C = c o s (θ) \cdot I 3 \times 3 - s i n (θ) ⌊ k \times ⌋ + (1 - c o s (θ)) k k T = (2 c o s 2 (θ / 2) - 1) \cdot I 3 \times 3 - 2 c o s (θ / 2) s i n (θ / 2) ⌊ k \times ⌋ + 2 s i n 2 (θ / 2) k k T

$\sideset{^L_G}{}C = cos(θ) · I_{3×3} − sin(θ)\lfloor {\large k}\times \rfloor+ (1 − cos(θ)) {\large k}{\large k}^T \\= (2 cos ^2 (θ/2)-1)· I_{3×3}-2cos(θ/2) sin(θ/2)\lfloor {\large k}\times\rfloor+ 2 sin^2 (θ/2) {\large k}{\large k}^T$
我们用四元数表示旋转矩阵

C L G C (q ̄) = ⎡ ⎣ ⎢ ⎢ q 21 - q 22 - q 23 + q 24 2 (q 1 q 2 - q 3 q 4) 2 (q 1 q 3 + q 2 q 4) 2 (q 1 q 2 + q 3 q 4) - q 21 + q 22 - q 23 + q 24 2 (q 2 q 3 - q 1 q 4) 2 (q 1 q 3 - q 2 q 4) 2 (q 2 q 3 + q 1 q 4) - q 21 - q 22 + q 23 + q 24 ⎤ ⎦ ⎥ ⎥ = ⎡ ⎣ ⎢ ⎢ 2 q 21 + 2 q 24 - 1 2 (q 1 q 2 - q 3 q 4) 2 (q 1 q 3 + q 2 q 4) 2 (q 1 q 2 + q 3 q 4) 2 q 22 + 2 q 24 - 1 2 (q 2 q 3 - q 1 q 4) 2 (q 1 q 3 - q 2 q 4) 2 (q 2 q 3 + q 1 q 4) 2 q 23 + 2 q 24 - 1 ⎤ ⎦ ⎥ ⎥ = ⎡ ⎣ ⎢ ⎢ 1 - 2 q 22 - 2 q 23 - 1 2 (q 1 q 2 - q 3 q 4) 2 (q 1 q 3 + q 2 q 4) 2 (q 1 q 2 + q 3 q 4) 1 - 2 q 21 - 2 q 23 2 (q 2 q 3 - q 1 q 4) 2 (q 1 q 3 - q 2 q 4) 2 (q 2 q 3 + q 1 q 4) 1 - 2 q 21 - 2 q 22 ⎤ ⎦ ⎥ ⎥

$\sideset{^L_G}{}C(q̄) = \begin{bmatrix}q_1^2 − q_2^2 − q_3^2 + q_4^2 & 2 (q_1q_2 + q_3 q_4) & 2 (q_1q_3 − q_2q_4 ) \\2 (q_1 q_2 − q_3 q_4 ) & −q_1^2 + q_2^2 − q_3^2 + q_4^2 & 2 (q_2 q_3 + q_1 q_4 )\\ 2 (q_1 q_3 + q_2 q_4 ) & 2 (q_2 q_3 − q_1 q_4 ) & −q_1^2 − q_2^2 + q_3^2 + q_4^2\end{bmatrix} \\ =\begin{bmatrix}2q_1^2 + 2q_4^2-1 & 2 (q_1q_2 + q_3 q_4) & 2 (q_1q_3 − q_2q_4 ) \\2 (q_1 q_2 − q_3 q_4 ) & 2 q_2^2 + 2q_4^2 -1& 2 (q_2 q_3 + q_1 q_4 )\\ 2 (q_1 q_3 + q_2 q_4 ) & 2 (q_2 q_3 − q_1 q_4 ) & 2q_3^2 + 2q_4^2-1\end{bmatrix}\\ =\begin{bmatrix}1-2q_2^2 - 2q_3^2-1 & 2 (q_1q_2 + q_3 q_4) & 2 (q_1q_3 − q_2q_4 ) \\2 (q_1 q_2 − q_3 q_4 ) & 1-2 q_1^2 - 2q_3^2 & 2 (q_2 q_3 + q_1 q_4 )\\ 2 (q_1 q_3 + q_2 q_4 ) & 2 (q_2 q_3 − q_1 q_4 ) & 1-2q_1^2 - 2q_2^2\end{bmatrix}$
旋转矩阵还有另一种表现形式

C L G C (q ̄) = I 3 \times 3 - 2 q 4 ⌊ q \times ⌋ + 2 ⌊ q \times ⌋ 2

$\sideset{^L_G}{}C(q̄) = {\large I}_{3\times3}-2q_4\lfloor{\large q}\times\rfloor+2\lfloor{\large q}\times\rfloor^2$
注意，由于四元组乘法的约定，两个旋转矩阵的乘积将对应于相同顺序的两个四元的乘积，因此

C L 1 L 2 C (q L 1 L 2 q ̄) \cdot C L 2 G C (q L 2 G q ̄) = C L 1 G C (q L 1 L 2 q ̄ \otimes q L 2 G q ̄)

$\sideset{^{L_1}_{L_2}}{}C(\sideset{^{L_1}_{L_2}}{}q̄)·\sideset{^{L_2}_{G}}{}C(\sideset{^{L_2}_{G}}{}q̄) = \sideset{^{L_1}_{G}}{}C(\sideset{^{L_1}_{L_2}}{}q̄⊗\sideset{^{L_2}_{G}}{}q̄)$
最终，我们可以解释

qL2L1q̄ =[ksin(θ/2)cos(θ/2)] $\sideset{^{L_2}_{L_1}}{}q̄ = \begin{bmatrix}{\large k} sin(θ/2)\\cos(θ/2)\end{bmatrix}$ 表示L2坐标系到L1坐标系的旋转，旋转轴K在L1中表示，这也可以表示为指数形式

C L 1 L 2 C (q ̄) = e x p (- ⌊ k \times ⌋ θ)

$\sideset{^{L_1}_{L_2}}{}C(q̄) = exp(−\lfloor {\large k} × \rfloor θ)$

1.5 四元数时间微分

当本地坐标系L相对全局坐标系G移动，我们可以计算改变率或者对应的四元数微分来描述他们的关系，我们通过计算差分式的极限

q L (t) G q ̄' (t) = lim ∆ t \to 0 1 ∆ t (q L (t + ∆ t) G q ̄ - q L (t) G q ̄)

$\sideset{^{L(t)}_{G}}{}q̄'(t) = \lim_{∆t \to 0} \frac{1}{∆t}(\sideset{^{L(t+∆t)}_{G}}{}q̄ -\sideset{^{L(t)}_{G}}{}q̄)$
四元数

qL(t+∆t)Gq̄ $\sideset{^{L(t+∆t)}_{G}}{}q̄$ 可以表示为两个寺院书叉乘

q L (t + ∆ t) G q ̄ = q L (t + ∆ t) t q ̄ \otimes q L (t) G q ̄

$\sideset{^{L(t+∆t)}_{G}}{}q̄ = \sideset{^{L(t+∆t)}_{t}}{}q̄⊗\sideset{^{L(t)}_{G}}{}q̄$
其中

q L (t + ∆ t) L (t) q ̄ = [k s i n (θ / 2) c o s (θ / 2)]

$\sideset{^{L(t+∆t)}_{L(t)}}{}q̄ = \begin{bmatrix}{\large k} sin(θ/2)\\cos(θ/2)\end{bmatrix}$

注意，四元数 $\sideset{^{L(t+∆t)}_{L(t)}}{}q̄$ 表示L(t)坐标系到L(t+∆t)坐标系的旋转，旋转角度为θ，旋转轴K是L(t+∆t)坐标系下的表示。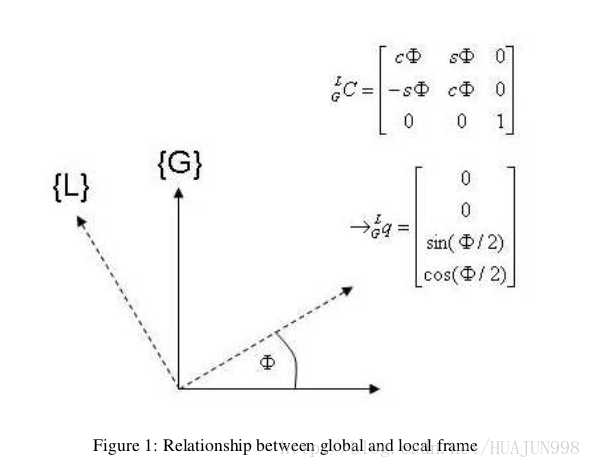这里写图片描述

在极限条件下，∆t → 0,旋转角度将会非常小，我们可以近似sin和cos函数用他们一阶泰勒展开式。

q L (t + ∆ t) L (t) q ̄ = [k s i n (θ / 2) c o s (θ / 2)] = [k θ / 2 1] = ⎡ ⎣ 1 2 \cdot δ θ 1 ⎤ ⎦

$\sideset{^{L(t+∆t)}_{L(t)}}{}q̄ = \begin{bmatrix}{\large k} sin(θ/2)\\cos(θ/2)\end{bmatrix}\\ =\begin{bmatrix}{\large k} θ/2\\1\end{bmatrix}\\ =\begin{bmatrix}\frac{1}{2}· δθ\\1\end{bmatrix}$
向量δθ与旋转轴同向，大小为旋转角度，将这个矢量除以∆t，极限时，得到旋转速度

ω = lim ∆ t \to 0 δ θ ∆ t

$ω = \lim_{∆t \to 0}\frac{δθ}{∆t}$

现在我们准备推出四元数的导数

q L (t) G q ̄' (t) = lim ∆ t \to 0 1 ∆ t (q L (t + ∆ t) G q ̄ - q L (t) G q ̄) \approx lim ∆ t \to 0 1 ∆ t (⎡ ⎣ 1 2 \cdot δ θ 1 ⎤ ⎦ - [01]) \otimes q L (t) G q ̄ = 1 2 [ω 1]) \otimes q L (t) G q ̄ = 1 2 [- ⌊ ω \times ⌋ - ω T ω 0] q L (t) G q ̄ = 1 2 Ω (ω) q L (t) G q ̄ = 1 2 Ξ (q L (t) G q ̄) ω

$\sideset{^{L(t)}_{G}}{}q̄'(t) = \lim_{∆t \to 0} \frac{1}{∆t}(\sideset{^{L(t+∆t)}_{G}}{}q̄ -\sideset{^{L(t)}_{G}}{}q̄)\\ \approx \lim_{∆t \to 0}\frac{1}{∆t}(\begin{bmatrix}\frac{1}{2}· δθ\\1\end{bmatrix}-\begin{bmatrix} 0 \\ 1\end{bmatrix})⊗\sideset{^{L(t)}_{G}}{}q̄\\ =\frac{1}{2}\begin{bmatrix} ω \\ 1\end{bmatrix})⊗\sideset{^{L(t)}_{G}}{}q̄\\ =\frac{1}{2}\begin{bmatrix} -\lfloor ω \times \rfloor & ω\\ -ω^T & 0\end{bmatrix}\sideset{^{L(t)}_{G}}{}q̄\\ = \frac{1}{2}Ω(ω)\sideset{^{L(t)}_{G}}{}q̄\\ = \frac{1}{2}Ξ(\sideset{^{L(t)}_{G}}{}q̄)ω$
其中

Ω (ω) = ⎡ ⎣ ⎢ ⎢ ⎢ ⎢ 0 - ω z ω y - ω x ω z 0 - ω x - ω y - ω y ω x 0 - ω z ω x ω y ω z 0 ⎤ ⎦ ⎥ ⎥ ⎥ ⎥

$Ω(ω) = \begin{bmatrix}0 & ω_z & -ω_y & ω_x\\ -ω_z & 0 & ω_x & ω_y \\ ω_y & -ω_x & 0 & ω_z\\-ω_x & -ω_y & -ω_z & 0\end{bmatrix}$

Ξ (q L (t) G q ̄) = ⎡ ⎣ ⎢ ⎢ ⎢ ⎢ q 4 q 3 - q 2 - q 1 - q 3 q 4 - q 1 - q 2 q 2 - q 1 q 4 - q 3 ⎤ ⎦ ⎥ ⎥ ⎥ ⎥

$Ξ(\sideset{^{L(t)}_{G}}{}q̄) =\begin{bmatrix}q_4 & -q_3 & q_2\\ q_3 & q_4 & -q_1 \\ -q_2 & -q_1 & q_4\\-q_1 & -q_2 & -q_3\end{bmatrix}$

注意 $ω = \sideset{^{L(t)}}{}ω$ ,换句话说旋转速度是本地的而不是惯性坐标系。

1.6 四元数积分

对四元数进行积分就相当于解一阶微分方程

q L G q ̄' (t) = 1 2 Ω (ω) q L G q ̄ (t)

$\sideset{^{L}_{G}}{}q̄'(t) = \frac{1}{2}Ω(ω)\sideset{^{L}_{G}}{}q̄(t)$
我们把时间从上标中去掉了，而表示时间变化四元数通过写q=q(t)来提高符号的清晰度。值得一提上标L表示时间t时的本地坐标系。
这个微分方程的通解

q L G q ̄' (t) = Θ (t, t k) q L G q ̄ (t k)

$\sideset{^{L}_{G}}{}q̄'(t) = Θ(t, t_k )\sideset{^{L}_{G}}{}q̄(t_k)$
微分和重新排序项得到了了

Θ(t,tk) $Θ(t, t_k )$ 的控制方程

Θ ̇ (t, t k) = q L G q ̄' (t) q L G q ̄ - 1 (t k) = 1 2 Ω (ω (t)) q L G q ̄ (t) q L G q ̄ - 1 (t k) = 1 2 Ω (ω (t)) Θ (t, t k)

$Θ̇(t, t k ) = \sideset{^{L}_{G}}{}q̄'(t)\sideset{^{L}_{G}}{}q̄^{-1}(t_k)\\ =\frac{1}{2}Ω(ω(t)) \sideset{^{L}_{G}}{}q̄(t)\sideset{^{L}_{G}}{}q̄^{-1}(t_k)\\ =\frac{1}{2}Ω(ω(t)) Θ(t, t k )$
其中初始条件

Θ (t k, t k) = I 4 \times 4

$Θ(t_k , t_k ) = I_{4×4}$
在确定的假设下我们可以获得这个等式的闭解形式，最简单的假设是ω在时间周期

∆t=tk+1−tk $∆t = t_k+1 − t_k$ 内是常数，使微分方程线性时不变，这个假设导致了零阶四元数积分。另一个更精确的近似是ω在∆t内是线性的，我们将把这个结果式的公式作为一阶四元数的积分。

1.6.1 零阶四元数积分

如果ω(t) = ω在积分周期 $∆t = t_{k+1} − t_ k$ 内是常数,矩阵Ω不依赖于时间， $Θ(t_{k+1} , t_k )$ 可以写成

Θ (t k + 1, t k) = Θ (∆ t) = e x p (1 2 Ω (ω) ∆ t)

$Θ(t_{k+1} , t_k ) = Θ(∆t) = exp(\frac{1}{2}Ω(ω)∆t)$
我们可以用泰勒级数展开成写矩阵的指数形式

Θ (∆ t) = I 4 \times 4 + 1 2 Ω (ω) ∆ t + 1 2 ! (1 2 Ω (ω) ∆ t) 2 + 1 3 ! (1 2 Ω (ω) ∆ t) 3 + . . .

$Θ(∆t) = {\large I}_{4\times4}+\frac{1}{2}Ω(ω)∆t+\frac{1}{2!}(\frac{1}{2}Ω(ω)∆t)^2+\frac{1}{3!}(\frac{1}{2}Ω(ω)∆t)^3+...$
利用Ω矩阵的性质得到

Θ (∆ t) = I 4 \times 4 + 1 2 Ω (ω) ∆ t - 1 2 ! (1 2 ∆ t) 2 | ω | 2 \cdot I 4 \times 4 - 1 3 ! (1 2 ∆ t) 3 | ω | 2 \cdot Ω (ω) + 1 4 ! (1 2 ∆ t) 4 | ω | 4 \cdot I 4 \times 4 + 1 5 ! (1 2 ∆ t) 5 | ω | 4 \cdot Ω (ω) - . . .

$Θ(∆t)={\large I}_{4\times4}+\frac{1}{2}Ω(ω)∆t-\frac{1}{2!}(\frac{1}{2}∆t)^2|ω|^2·{\large I}_{4\times4}-\frac{1}{3!}(\frac{1}{2}∆t)^3|ω|^2· Ω(ω)+\frac{1}{4!}(\frac{1}{2}∆t)^4|ω|^4·{\large I}_{4\times4}+\frac{1}{5!}(\frac{1}{2}∆t)^5|ω|^4· Ω(ω)-...$
重新排列和展开|ω|得到

Θ (∆ t) = (1 - 1 2 ! (1 2 ∆ t) 2 | ω | 2 + 1 4 ! (1 2 ∆ t) 4 | ω | 4 - . . .) I 4 \times 4 + 1 | ω | (1 2 | ω | ∆ t - 1 3 ! (1 2 | ω | ∆ t) 3 + 1 5 ! (1 2 | ω | ∆ t) 5) - . . .) Ω (ω)

$Θ(∆t) = (1-\frac{1}{2!}(\frac{1}{2}∆t)^2|ω|^2 + \frac{1}{4!}(\frac{1}{2}∆t)^4|ω|^4-...){\large I}_{4\times4} + \frac{1}{|ω|}(\frac{1}{2}|ω|∆t-\frac{1}{3!}(\frac{1}{2}|ω|∆t)^3+\frac{1}{5!}(\frac{1}{2}|ω|∆t)^5)-...)Ω(ω)$
经过仔细检查，我们发现了泰勒级数展开式的sin和cos函数

Θ (∆ t) = c o s (| ω | 2 ∆ t) \cdot I 4 \times 4 + 1 | ω | s i n (| ω | 2 ∆ t) \cdot Ω (ω)

$Θ(∆t) = cos(\frac{|ω|}{2}∆t)·{\large I}_{4\times4}+\frac{1}{|ω|}sin(\frac{|ω|}{2}∆t)· Ω(ω)$
最终我们可以写零阶四元数积分

q L G q ̄ (t k + 1) = Θ (t k + 1, t k) q L G q ̄ (t k) = (c o s (| ω | 2 ∆ t) \cdot I 4 \times 4 + 1 | ω | s i n (| ω | 2 ∆ t) \cdot Ω (ω)) q L G q ̄ (t k)

$\sideset{^{L}_{G}}{}q̄(t_{k+1}) = Θ(t_{k+1} , t_k )\sideset{^{L}_{G}}{}q̄(t_k)\\ =(cos(\frac{|ω|}{2}∆t)·{\large I}_{4\times4}+\frac{1}{|ω|}sin(\frac{|ω|}{2}∆t)· Ω(ω))\sideset{^{L}_{G}}{}q̄(t_k)$
仔细观察就会发现

Θ(tk+1,tk) $Θ(t_{k+1} , t_k )$ 不过是一个与特定四元数相关的乘法矩阵，
这样我们就可以把零阶四元数的积分改写成四元数的乘积

q L G q ̄ (t k + 1) = ⎡ ⎣ ⎢ ⎢ ⎢ ω | ω | \cdot s i n (| ω | 2 ∆ t) c o s (| ω | 2 ∆ t) ⎤ ⎦ ⎥ ⎥ ⎥ \otimes q L G q ̄ (t k)

$\sideset{^{L}_{G}}{}q̄(t_{k+1}) =\begin{bmatrix}\frac{ω}{|ω|}\cdot sin(\frac{|ω|}{2}∆t)\\ cos(\frac{|ω|}{2}∆t)\end{bmatrix}⊗\sideset{^{L}_{G}}{}q̄(t_k)$
这个四元数的乘积对应于将原始坐标系沿旋转轴ω旋转|ω|∆t角度，它对应于ω是常数的假设。
上面的表达式对于极小的ω可会造成数字不稳定，因为|ω|出现在分母当中，我们将计算上式的极限|ω|趋近于0，利用L’Hôpital定理计算乘

lim | ω | \to 0 Θ (∆ t) = lim | ω | \to 0 (c o s (| ω | 2 ∆ t) I 4 \times 4 + 1 | ω | s i n (| ω | 2 ∆ t) Ω (ω)) = I 4 \times 4 + lim | ω | \to 0 (1 | ω | s i n (| ω | 2 ∆ t) Ω (ω)) = I 4 \times 4 + ∆ t 2 Ω (ω)

$\lim_{|ω| \to 0}Θ(∆t) = \lim_{|ω| \to 0}(cos(\frac{|ω|}{2}∆t){\large I}_{4\times4}+\frac{1}{|ω|}sin(\frac{|ω|}{2}∆t)Ω(ω))\\ ={\large I}_{4\times4} + \lim_{|ω| \to 0}(\frac{1}{|ω|}sin(\frac{|ω|}{2}∆t)Ω(ω) )\\ ={\large I}_{4\times4}+\frac{∆t}{2}Ω(ω)$

1.6.2 一阶四元数积分

一阶四元数积分假设ω在积分区间∆t内是线性变化的，在这种情况下我们必须改变上面的 $Θ(t_{k+1} , t_k )$ ,为了这个目的，我们将引入平均旋转率ω̄，定义为

ω ̄ = ω ( t k + 1 ) + ω ( t k ) 2

$ω̄ =\frac{ω(t_{k+1} ) + ω(t_k )}{2}$
我们也定义了旋转率的微分ω’和相关的Ω( ω’)矩阵，在现行条件下是常数。

Ω (ω') = Ω (ω ( t k + 1 ) - ω ( t k ) ∆ t)

$Ω( ω') =Ω(\frac{ω(t_{k+1} ) − ω(t_k )}{∆t})$
注意高阶的Ω( ω) 微分是零。
为了计算

tk+1 $t_{k+1}$ 时的四元数，我们写下她在时间

tk $t_k$ 时的泰勒展开

q L G q ̄ (t k + 1) = q L G q ̄ (t k) + q L G q ̄' (t k) ∆ t + 1 2 q L G q ̄'' (t k) ∆ t 2 + . . .

$\sideset{^{L}_{G}}{}q̄(t_{k+1}) = \sideset{^{L}_{G}}{}q̄(t_{k}) + \sideset{^{L}_{G}}{}q̄'(t_{k}) ∆t+\frac{1}{2}\sideset{^{L}_{G}}{}q̄''(t_{k}) ∆t^2+...$

重复的利用四元数时间微分的定义得到

q L G q ̄ (t k + 1) = (I 4 \times 4 + 1 2 Ω (ω (t k)) ∆ t + 1 2 ! (Ω (ω (t k)) ∆ t)) 2 + 1 3 ! (Ω (ω (t k)) ∆ t)) 3 + . . .) q L G q ̄ (t k) + 1 4 ∆ t 2 Ω (ω' (t k)) q L G q ̄ (t k) + (1 12 Ω (ω' (t k)) Ω (ω (t k)) + (1 24 Ω (ω (t k)) Ω (ω' (t k))) ∆ t 3 q L G q ̄ (t k) + . . .

$\sideset{^{L}_{G}}{}q̄(t_{k+1}) = ({\large I}_{4\times4}+\frac{1}{2}Ω(ω(t_k))∆t + \frac{1}{2!}(Ω(ω(t_k))∆t))^2+ \frac{1}{3!}(Ω(ω(t_k))∆t))^3+...)\sideset{^{L}_{G}}{}q̄(t_{k}) + \frac{1}{4}∆t^2 Ω( ω'(t k ))\sideset{^{L}_{G}}{}q̄(t_{k})+(\frac{1}{12}Ω(ω'(t_k))Ω(ω(t_k))+(\frac{1}{24}Ω(ω(t_k))Ω(ω'(t_k)))∆t^3\sideset{^{L}_{G}}{}q̄(t_{k})+...$
如果我们将Ω( ω̄)均值写成

Ω (ω ̄) = 1 ∆ t \int t k + 1 t k Ω (ω (τ)) d τ = Ω (ω (t k)) + 1 2 Ω (ω' (t k)) ∆ t

$Ω( ω̄) = \frac{1}{∆t}\int_{t_k}^{t_{k+1}}Ω(ω(τ )){\rm d}τ \\= Ω(ω(t_k ))+\frac{1}{2}Ω( ω'(t_k ))∆t$
我们可以重新排列项

q L G q ̄ (t k + 1) = (I 4 \times 4 + 1 2 Ω (ω ̄) ∆ t + 1 2 ! (Ω (ω ̄) ∆ t)) 2 + 1 3 ! (Ω (ω ̄) ∆ t)) 3 + . . . + 1 48 (Ω (ω' (t k)) Ω (ω (t k)) - Ω (ω (t k)) Ω (ω' (t k))) ∆ t 3) q L G q ̄ (t k)

$\sideset{^{L}_{G}}{}q̄(t_{k+1}) =({\large I}_{4\times4}+\frac{1}{2}Ω(ω̄)∆t + \frac{1}{2!}(Ω(ω̄)∆t))^2+ \frac{1}{3!}(Ω(ω̄)∆t))^3+...+\frac{1}{48}(Ω( ω'(t_k ))Ω(ω(t_k ))-Ω(ω(t_k ))Ω( ω'(t_k )))∆t^3)\sideset{^{L}_{G}}{}q̄(t_{k})$

我们发现第一项是指数的泰勒级数展开，带入Ω( ω’)，我们或的最终公式

q L G q ̄ (t k + 1) = (e x p (1 2 Ω (ω ̄) ∆ t) + 1 48 (Ω (ω (t k + 1)) Ω (ω (t k)) - Ω (ω (t k)) Ω (ω (t k + 1))) ∆ t 2) q L G q ̄ (t k)

$\sideset{^{L}_{G}}{}q̄(t_{k+1}) = (exp(\frac{1}{2}Ω( ω̄)∆t)+\frac{1}{48}(Ω(ω(t_{k+1}))Ω(ω(t_k))-Ω(ω(t_k))Ω(ω(t_{k+1})))∆t^2)\sideset{^{L}_{G}}{}q̄(t_{k})$

2 姿态传播

卡尔曼滤波器估计当前姿态包含两步。在第一步，传播，滤波器预测当前的姿态基于上一次估计和一些本体感受的测量，这个估计在后面的更新步中被修正，当的到一个新的绝对方位测量。
预测系统状态的一种方法是将系统中给定的控制命令输入到系统模型中，从而预测系统的行为。另一种估计位置和方向的方法是使用惯性测量单元(IMU)的数据作为动态模型替换。IMU提供了对系统上的平移加速度和旋转速度的测量。本文将探讨后一种方法。在讨论状态方程和误差传播之前，我们将描述陀螺仪的模型，它将提供旋转速度的测量值。

2.1 陀螺仪噪声模型

作为IMU的一部分，一个三轴陀螺仪提供了旋转速度的测量。众所周知，陀螺会受到不同的误差项影响，例如速率噪声误差和偏差。我们使用一个简单的模型将测量的旋转速率 $ω_m$ 和实际的角速度 $ω$ 联系起来

ω m = ω + b + n r

$ω_m = ω + b + n_r$
在这个等式中，

b $b$ 表示陀螺仪偏置，

nr $n_r$ 表示噪声系数，假设是高斯白噪声，具有如下特性

E [n r] = 0 3 \times 1 E [n r (t + τ) n T r (t) = N r δ (τ)

$E [n_r ] = 0_{3×1}\\ E [n_r (t + τ )n_r^T (t) = N_r δ(τ )$
陀螺偏差是非静态的，并模拟为随机游走过程

b' = n w

$b' = n_w$
具有如下属性

E [n w] = 0 3 \times 1 E [n r (t + τ) n T r (t)] = N r δ (τ)

$E [n_w ] = 0_{3\times1}\\ E[n_r (t + τ )n_r^T (t)]=N_r δ(τ )$
因此，偏差是随机的，需要和四元数一起估计。
为了简化我们假设噪声在三个方向是相等的

N r = σ 2 r c \cdot I 3 \times 3 N r = σ 2 w c \cdot I 3 \times 3

$N_r= σ^2_{rc} · I_{3×3}\\ N_r= σ^2_{wc} · I_{3×3}$
下标c表示，这些是连续时间系统的噪声协方差，将它们与后面离散系统中的噪声协方差进行了区分。
为了确定协方差的单位，我们考虑了标量的例子，它直接扩展到向量的情况。为了兼容性，

nr $n_r$ 与ω有相同的单位，因此

[E [n r (t + τ) n r (t)]] = [σ 2 r c δ (τ)] = r a d 2 s e c 2

$[E[n_r(t+τ)n_r(t)]] = [σ^2_{rc}δ(τ )] = \frac{rad^2}{sec^2}$ 但是

δ(τ) $δ(τ )$ 的单位定义为

[δ (τ)] = 1 s e c

$[δ(τ )] =\frac{1}{sec}$ 因此

[σ 2 r c] = r a d 2 s e c 2 \cdot s e c = r a d s e c 2 \cdot 1 1 s e c = r a d s e c 2 \cdot 1 H z

$[σ^2_{rc}] = \frac{rad^2}{sec^2}\cdot sec\\ = \frac{rad}{sec}^2\cdot\frac{1}{\frac{1}{sec}}\\ =\frac{rad}{sec}^2\cdot\frac{1}{Hz}$
并且

[σ r c] = (r a d s e c) \cdot 1 H z - - - \sqrt = r a d s e c - - - \sqrt

$[σ_{rc}] = (\frac{rad}{sec})\cdot \frac{1}{\sqrt{Hz}}= \frac{rad}{\sqrt{sec}}$
分析得到

[σ 2 w c] = (r a d s e c / s e c) 2 \cdot s e c = r a d 2 s e c 3 = (r a d s e c) 2 \cdot H z

$[σ^2_{wc}] =(\frac{rad}{sec}/sec)^2\cdot sec\\ =\frac{rad^2}{sec^3}\\ =(\frac{rad}{sec})^2\cdot Hz$
并且

[σ w c] = (r a d s e c) \cdot H z - - - \sqrt = r a d s e c 3 - - - - \sqrt

$[σ_{wc}] = (\frac{rad}{sec})\cdot {\sqrt{Hz}}= \frac{rad}{\sqrt{sec^3}}$
在离散情况下，

nrd $n_{rd}$ 和

nwd $n_{wd}$ 必须有与旋转速率相同的单位,也就是rad/sec。为了保持噪声强度的等效性，我们必须在离散化的情况下加入采样频率，得到

σ r d = σ r c ∆ t - - \sqrt σ w d = σ w c \cdot ∆ t - - \sqrt

$σ_{rd} = \frac{σ_{rc}}{\sqrt{∆t}}\\ σ_{wd} = σ_{wc}\cdot \sqrt{∆t}$
其中∆t是采样频率的倒数，离散方差将用于模拟真实世界的数据。关于连续和离散噪声变化之间的转换的进一步解释是由Simon提供的。为了与书中推导进行类比，偏差噪声，

nw $n_w$ ，对应于过程噪声，而速率噪声，

nr $n_r$ ，对应于测量噪声。

2.2 状态方程

在之前的分析的结果中，我们定义了一个七个元素的状态向量,由四元数和陀螺偏差组成的

x (t) = [q ̄ (t) b (t)]

$x(t) = \begin{bmatrix}q̄(t)\\ {\large b}(t)\end{bmatrix}$
由四元数微分的定义和误差模型，我们找到以下微分方程组控制的状态

q L G q ̄' (t) = 1 2 Ω (ω m - b - n r) q L G q ̄ (t) b' = n w

$\sideset{^{L}_{G}}{}q̄'(t) = \frac{1}{2}Ω(ω_m − b − n_r ) \sideset{^{L}_{G}}{}q̄(t)\\ b'=n_w$ 以上述的期望为目标，在ekf框架内为状态提供预测方程(cf 3，422)。

q L G q c' (t) = 1 2 Ω (ω c) q L G q c (t) b' c = 0 3 \times 3

$\sideset{^{L}_{G}}{_c}q'(t)=\frac{1}{2}Ω(ω_c )\sideset{^{L}_{G}}{_c}q(t)\\ b_c' = 0_{3\times3}$
其中

ω c = ω m - b

$ω_c = ω_m − b$ 由于在积分区间上的偏差是恒定的，我们可以使用零阶或第一阶积分来积分四元数，用

ωc $ω_c$ 代替

ω $ω$ 。

2.3 误差和协方差表示

通常，误差向量及其协方差是由状态向量和它的估计之间的算术差来表示的。然而，在手边的问题中，由于系统中存在约束，这种表示是有问题的。由于四元数被强制成单位长度使得对应的协方差矩阵是奇异的，很难维持它的数值性，为了稳定的原因，我们将用一个不同的六维的误差向量表示方法。
不使用四元数与四元数估计之间的算数差来定义误差，我们引入一个四元数误差 $δq_c$ ;一个很小的旋转在估计和真正的本地参考坐标系之间，我们定义一个乘积来表示误差代替差分

q L G q ̄ = δ L L c δ q ̄ \otimes q L G q c δ L L c δ q ̄ = q L G q ̄ \otimes q L G q - 1 c

$\sideset{^{L}_{G}}{}q̄ = \sideset{^{L}_{L_c}}{}δq̄⊗\sideset{^{L}_{G}}{_c}q\\ \sideset{^{L}_{L_c}}{}δq̄ = \sideset{^{L}_{G}}{}q̄ ⊗\sideset{^{L}_{G}}{^{-1}_c}q$
由于与误差四元数相关的旋转可以被认为是非常小的，我们可以用一个小的角度近似，并且定义姿态误差角向量

δθ $δθ$ 如下

δ q ̄ = [δ q δ q 4] = [k s i n (δ θ / 2) c o s (δ θ / 2)] \approx ⎡ ⎣ 1 2 δ θ 1 ⎤ ⎦

$δq̄ = \begin{bmatrix}δ{\large q}\\ δq_4\end{bmatrix}\\ =\begin{bmatrix}{\large k}sin(δθ/2)\\ cos(δθ/2)\end{bmatrix}\\ \approx \begin{bmatrix}\frac{1}{2}δθ\\ 1\end{bmatrix}$
误差角向量δθ 是

3×1 $3\times1$ 维度的，将和偏置误差一起在误差状态向量中使用，偏置误差定义为

∆ b = b - b c

$∆b = b − b_c$ 我们可以定义误差向量

x = [δ θ ∆ b]

$x =\begin{bmatrix}δθ\\ ∆b\end{bmatrix}$
在下一节我们将研究误差向量的连续时间状态方程。

2.4 连续时间状态方程

为了推导出误差向量的连续时间线性状态方程，我们将从误差四元的定义开始

q ̄ = δ q ̄ \otimes q c q' c = δ' q ̄ \otimes q ̄ + δ q ̄ \otimes q' c

$q̄ = δq̄ ⊗ q_c\\ q_c' = δ'q̄⊗q̄+δq̄ ⊗ q_c'$
用

q′ $q'$ 定义和

q′c $q_c'$ 定义代替可以得到

1 2 [ω 0] \otimes q ̄ = δ' q ̄ \otimes q ̄ + δ q ̄ \otimes （ 1 2 [ω c 0] \otimes q c) δ' q ̄ \otimes q c = 1 2 ([ω 0] \otimes q ̄ - （ δ q ̄ ） \otimes [ω c 0] \otimes q c) δ' q ̄ = 1 2 ([ω 0] \otimes δ q ̄ - δ q ̄ \otimes [ω c 0])

$\frac{1}{2}\begin{bmatrix}ω\\0\end{bmatrix}⊗q̄ = δ'q̄⊗q̄+δq̄ ⊗（\frac{1}{2}\begin{bmatrix}ω_c\\0\end{bmatrix}⊗ q_c)\\ δ'q̄⊗q_c = \frac{1}{2}(\begin{bmatrix}ω\\0\end{bmatrix}⊗q̄-（δq̄）⊗\begin{bmatrix}ω_c\\0\end{bmatrix}⊗ q_c) \\ δ'q̄ = \frac{1}{2}(\begin{bmatrix}ω\\0\end{bmatrix}⊗δq̄ -δq̄ ⊗\begin{bmatrix}ω_c\\0\end{bmatrix})$
联系陀螺仪模型

ω $ω$ 和

ωc $ω_c$ 的定义，得到

ω = ω c - ∆ b - n r

$ω = ω_c−∆b − n_r$

在上面的替换中

δ' q ̄ = 1 2 ([ω c 0] \otimes δ q ̄ - δ q ̄ \otimes [ω c 0]) - 1 2 [∆ b + n r 0] \otimes δ q ̄ = 1 2 ([- ⌊ ω c \times ⌋ - ω T c ω c 0] \otimes (δ q ̄) - [⌊ ω c \times ⌋ - ω T c ω c 0] \otimes δ q ̄) -) - 1 2 [∆ b + n r 0] \otimes δ q ̄ = 1 2 [- 2 ⌊ ω c \times ⌋ 0 1 \times 3 0 3 \times 1 0] \cdot (δ q ̄) - 1 2 [∆ b + n r 0] \otimes δ q ̄ = 1 2 [- 2 ⌊ ω c \times ⌋ 0 1 \times 3 0 3 \times 1 0] \cdot (δ q ̄) - 1 2 [∆ b + n r 0] - O (| ∆ b | | δ q |, | n r | | δ q |)

$δ'q̄ = \frac{1}{2}(\begin{bmatrix}ω_c\\0\end{bmatrix}⊗δq̄-δq̄⊗\begin{bmatrix}ω_c\\0\end{bmatrix})-\frac{1}{2}\begin{bmatrix}∆b + n_r\\0\end{bmatrix}⊗δq̄\\ = \frac{1}{2}(\begin{bmatrix}-\lfloor ω_c\times\rfloor & ω_c\\-ω^T_c & 0\end{bmatrix}⊗(δq̄)-\begin{bmatrix}\lfloor ω_c\times\rfloor & ω_c\\-ω^T_c & 0\end{bmatrix}⊗δq̄)-)-\frac{1}{2}\begin{bmatrix}∆b + n_r\\0\end{bmatrix}⊗δq̄\\ =\frac{1}{2}\begin{bmatrix}-2\lfloor ω_c\times\rfloor & 0{3\times1}\\0_{1\times3} & 0\end{bmatrix}\cdot(δq̄)-\frac{1}{2}\begin{bmatrix}∆b + n_r\\0\end{bmatrix}⊗δq̄\\ =\frac{1}{2}\begin{bmatrix}-2\lfloor ω_c\times\rfloor & 0_{3\times1}\\0_{1\times3} & 0\end{bmatrix}\cdot(δq̄)-\frac{1}{2}\begin{bmatrix}∆b + n_r\\0\end{bmatrix}-O(|∆b||δq|, |n_r||δq|)$
忽略二阶项，我们可以写成

δ' q ̄ = [δ' q δ' q 4] = ⎡ ⎣ 1 2 δ' θ 1' ⎤ ⎦ = ⎡ ⎣ - ω c \times δ q - 1 2 (∆ b + n r) 0 ⎤ ⎦

$δ'q̄ =\begin{bmatrix}δ'{\large q}\\δ'q_4\end{bmatrix}=\begin{bmatrix}\frac{1}{2}δ'θ\\1'\end{bmatrix}=\begin{bmatrix}−ω_c\times δq-\frac{1}{2}(∆b + n_r)\\0\end{bmatrix}$
最终

δ' θ = - ω c \times δ θ - ∆ b - n r

$δ'θ = −ω_c × δθ −∆b − n_r$
偏置误差的控制方程很容易计算出来

∆' b = b' - b c = n w

$∆'b = b' − b_c = n_w$
联系这些结果我们可以重写误差状态方程

= [δ' θ ∆' b] = [- ⌊ ω c \times ⌋ 0 3 \times 3 I 3 \times 3 0 3 \times 3] \cdot [δ θ ∆ b] + [- I 3 \times 3 0 3 \times 3 0 3 \times 3 0 3 \times 3] \cdot [n r n w]

$=\begin{bmatrix}δ'θ\\∆'b \end{bmatrix} =\begin{bmatrix}-\lfloor ω_c\times\rfloor & I_{3\times3}\\0_{3\times3} & 0_{3\times3} \end{bmatrix}\cdot \begin{bmatrix}δθ\\∆b\end{bmatrix}+\begin{bmatrix}-I_{3\times3} & 0_{3\times3}\\0_{3\times3} & 0_{3\times3} \end{bmatrix}\cdot\begin{bmatrix}n_r\\n_w \end{bmatrix}$
或者

x' = F c \cdot x + G c \cdot n

$x' = F_c · x +G_c · n$
其中

F c = [- ⌊ ω c \times ⌋ 0 3 \times 3 I 3 \times 3 0 3 \times 3] G c = [- I 3 \times 3 0 3 \times 3 0 3 \times 3 0 3 \times 3]

$F_c=\begin{bmatrix}-\lfloor ω_c\times\rfloor & I_{3\times3}\\0_{3\times3} & 0_{3\times3} \end{bmatrix}\\ G_c=\begin{bmatrix}-I_{3\times3} & 0_{3\times3}\\0_{3\times3} & 0_{3\times3} \end{bmatrix}$
是系统矩阵和噪声矩阵

x = [δ θ ∆ b], n = [n r n w]

$x = \begin{bmatrix}δθ\\∆b \end{bmatrix},n=\begin{bmatrix}n_r\\n_w \end{bmatrix}$
分别表示误差状态和噪声向量。
就像我们在2.1节中讨论的，假设

nr $n_r$ 和

nw $n_w$ 是白噪声且独立的，连续系统噪声协方差矩阵就是

Q c = E [n (t + τ) n T (t)] = [N r 0 3 \times 3 0 3 \times 3 N w] = [σ 2 r c \cdot I 3 \times 3 0 3 \times 3 0 3 \times 3 σ 2 w c]

$Q_c = E[n(t + τ)n^T(t)] = \begin{bmatrix}N_r & 0_{3\times3}\\0_{3\times3} & N_w \end{bmatrix} = \begin{bmatrix}σ^2_{rc}\cdot I_{3\times3}&0_{3\times3}\\0_{3\times3} & σ^2_{wc}\end{bmatrix}$

2.5 离散时间误差状态方程

为了实现离散时间卡尔曼滤波方程，我们需要对上述误差传播模型进行离散化处理。特别是，我们需要找到状态转换矩阵Φ和系统噪声协方差 $Q_d$ 。

3D姿态估计-间接卡尔曼滤波

1 四元数代数中的元素

1.1 四元数定义

1.2 四元数乘法

1.3 有用的性质

1.3.1 叉乘反对称矩阵 $\lfloor \omega\times \rfloor$ 的属性

1.3.2 Ω矩阵的性质

1.3.3 Ξ矩阵的性质

1.4 四元数和旋转矩阵之间的关系

1.5 四元数时间微分

1.6 四元数积分

1.6.1 零阶四元数积分

1.6.2 一阶四元数积分

2 姿态传播

2.1 陀螺仪噪声模型

2.2 状态方程

2.3 误差和协方差表示

2.4 连续时间状态方程

2.5 离散时间误差状态方程

2.5.1 状态转换矩阵

猜你喜欢

3D姿态估计-间接卡尔曼滤波

1 四元数代数中的元素

1.1 四元数定义

1.2 四元数乘法

1.3 有用的性质

1.3.1 叉乘反对称矩阵 ⌊ω×⌋ \lfloor \omega\times \rfloor的属性

1.3.2 Ω矩阵的性质

1.3.3 Ξ矩阵的性质

1.4 四元数和旋转矩阵之间的关系

1.5 四元数时间微分

1.6 四元数积分

1.6.1 零阶四元数积分

1.6.2 一阶四元数积分

2 姿态传播

2.1 陀螺仪噪声模型

2.2 状态方程

2.3 误差和协方差表示

2.4 连续时间状态方程

2.5 离散时间误差状态方程

2.5.1 状态转换矩阵

猜你喜欢

1.3.1 叉乘反对称矩阵 $\lfloor \omega\times \rfloor$ 的属性