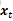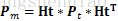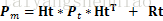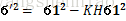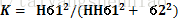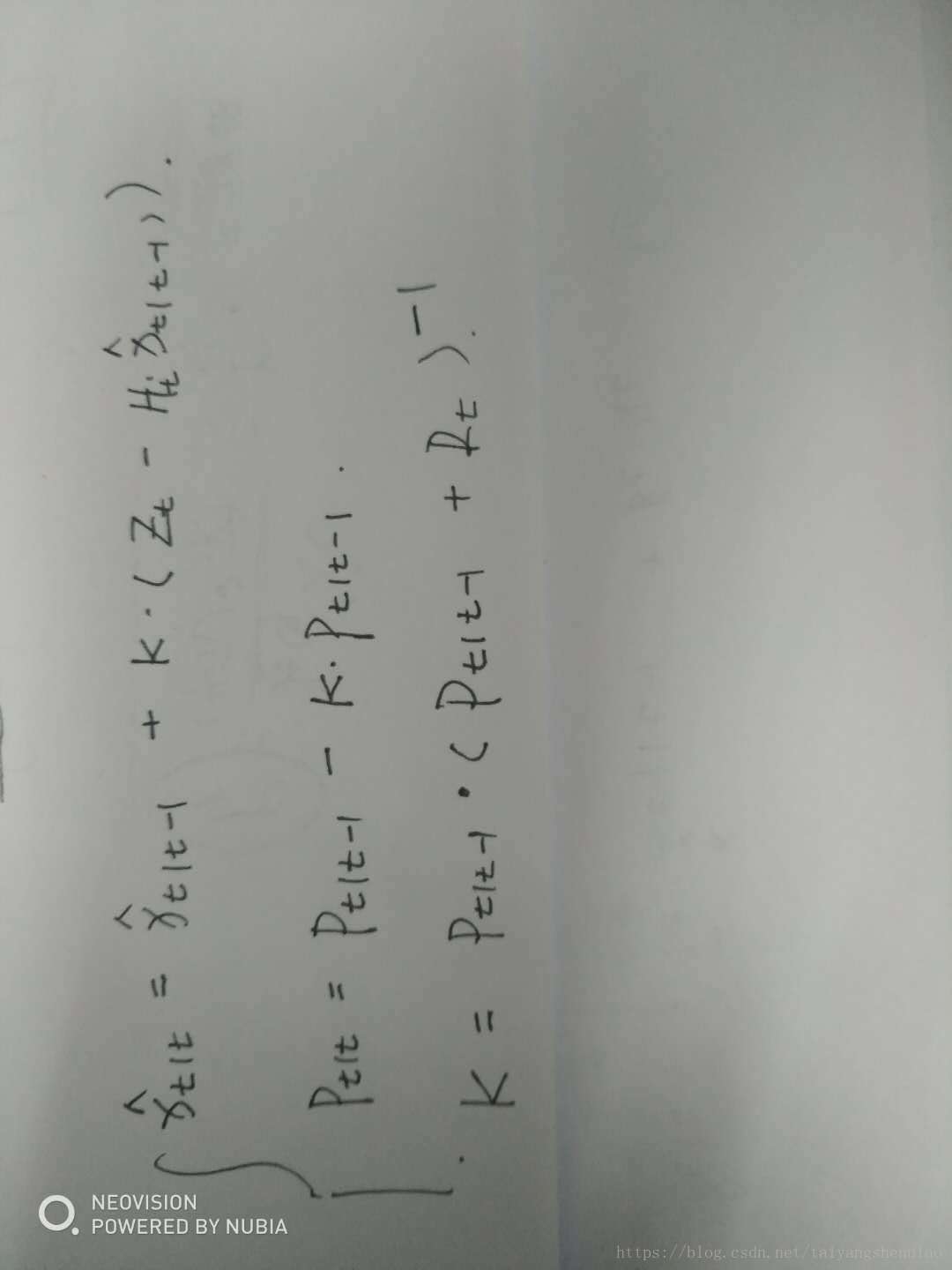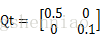卡尔曼滤波说明
什么是卡尔曼滤波:
你可以在任何含有不确定因素的动态系统里使用卡尔曼滤波,而且你应该可以通过某种数学建模对系统下一步动向做一个大概的预测。尽管系统总是会受到一些未知的干扰,但是卡尔曼滤波总是可以派上用场来提高系统预估的精确度,这样你就可以更加准确地知道到底发生了什么事情(系统状态是如何转移的)。
卡尔曼是使用已有的测量数据和观测数据,再结合两者这件的协方差等参数估计系统下一步状态的一种计算方法。
原理理解和过程推导:
既然卡尔曼是结合观测数据和预测数据来确定当前目标的最有位置,那么首先需要做的,就是对系统进行建模。
假设系统的状态空间中包括了距离和速度两项。即x = [r v]’;系统以匀加速运动,系统加速度a = 1;根据牛顿运动定律可预测目标的当前位置为:
rt= rt-1+vt-1*△t+(a*△t2
vt= vt-1 + a*△t
结合上述两方程使用矩阵乘法形式表示如下所示:
rtvt= 1△t01rt-1vt-1+ △t22△t*a
令Ft = 1△t01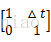

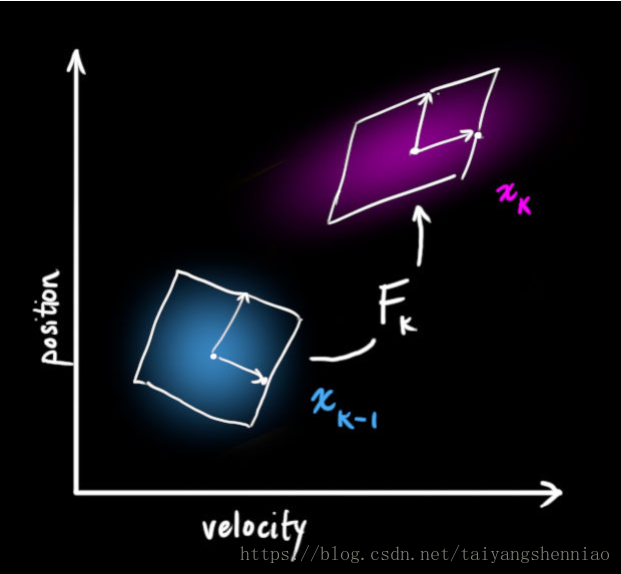
Ft和Bt矩阵的作用是通过上一次的位置,将目标计算到下一次位置。如下图所示:
由于在xk-1的位置上距离和速度是存在相关性的,应为随着速度的变化,距离也是会随之变化的。假设在xt-1


根据对称矩阵的性质可以知道,假设:
covx=p
则covAx=ApAT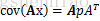
所以系统从xk-1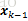
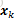

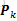
其中Pt=Ft*Pt-1*FtT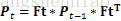
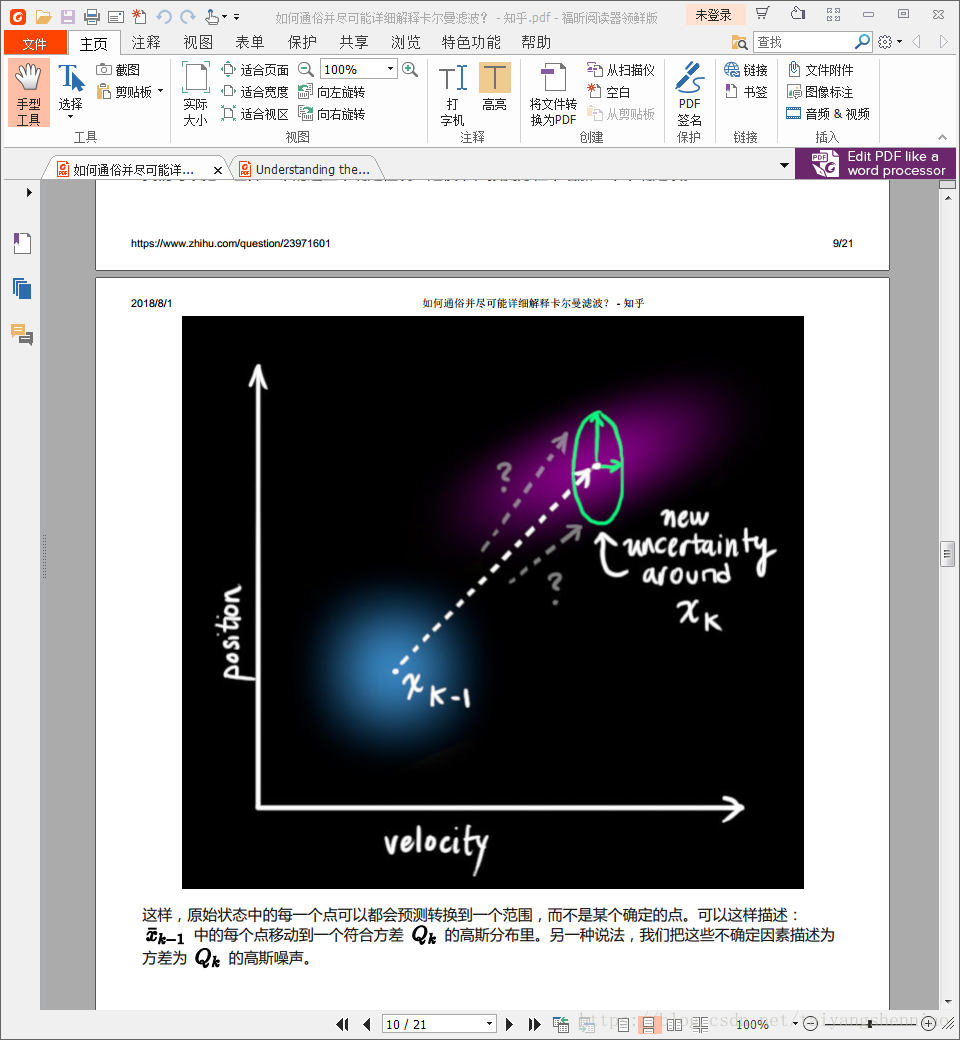
综上表达式1和表达式2就已经完成了目标的预测的过程。当时上述过程还少了一个误差量。这个误差量有可能是系统本身自带的或者是计算机的浮点误差或是截位误差等等。通俗来讲就是说,理论上xt-1
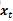
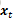
这个误差我们使用Qt
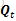
此处需要区分两个概念,一个是Pt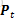
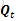

Pt=Ft*Pt-1*FtT+ Qt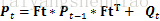
//***************************************************************************************//
上面一部分是介绍系统的预测值。并且得到了系统预测值得协方差矩阵,下面一部分就是关系系统的测量值:
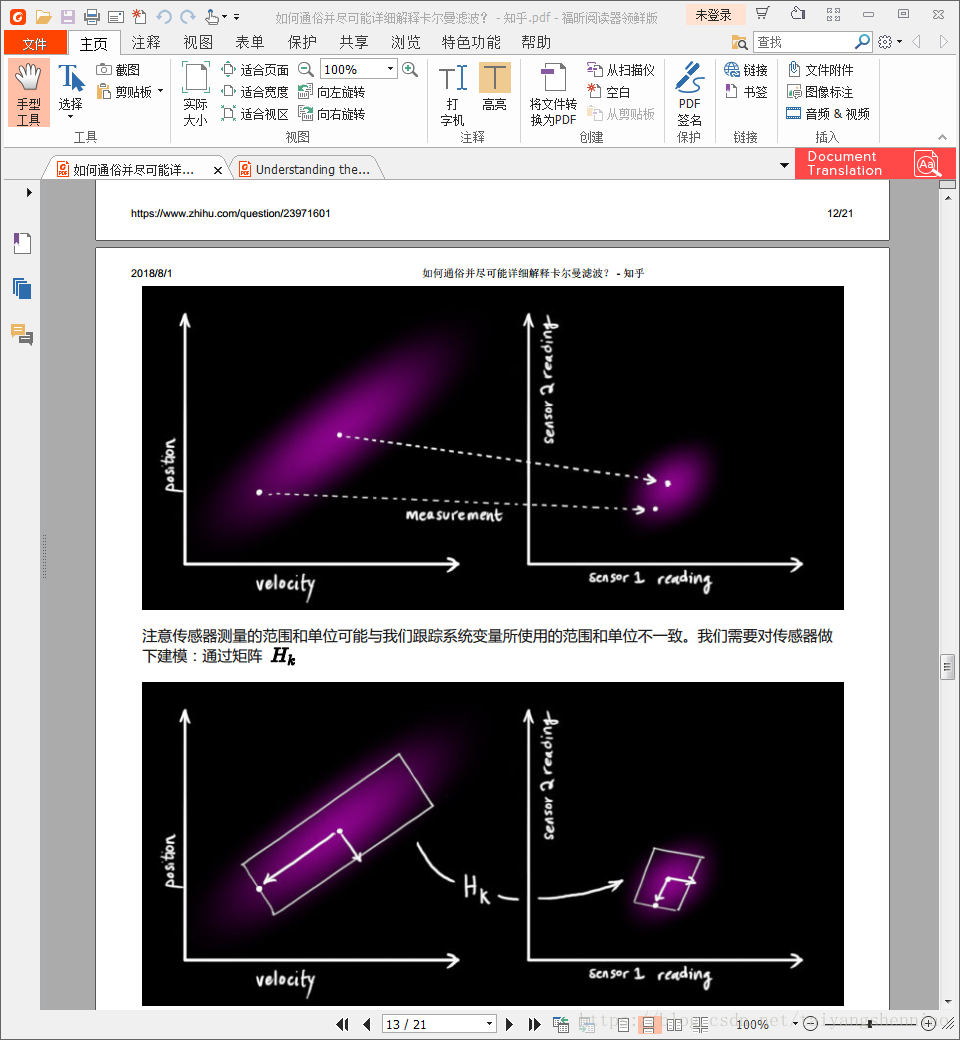
一般情况下我们通过传感器就能够直接测量得到我们的状态空间中的变量。比如雷达能够直接测量得到距离和速度,而距离和速度就是系统状态空间中的变量。但是也不排除传感器测量的量并不是我们状态系统中的变量。比如说,雷达传感器无法直接测量出前方目标的加速度,只能通过测量得到的速度和时间间隔通过公式计算出加速度。那么这个计算也可以通过矩阵来建模,这个变换矩阵称之为Ht矩阵。如下图所示:
对于测量值而言:
xm
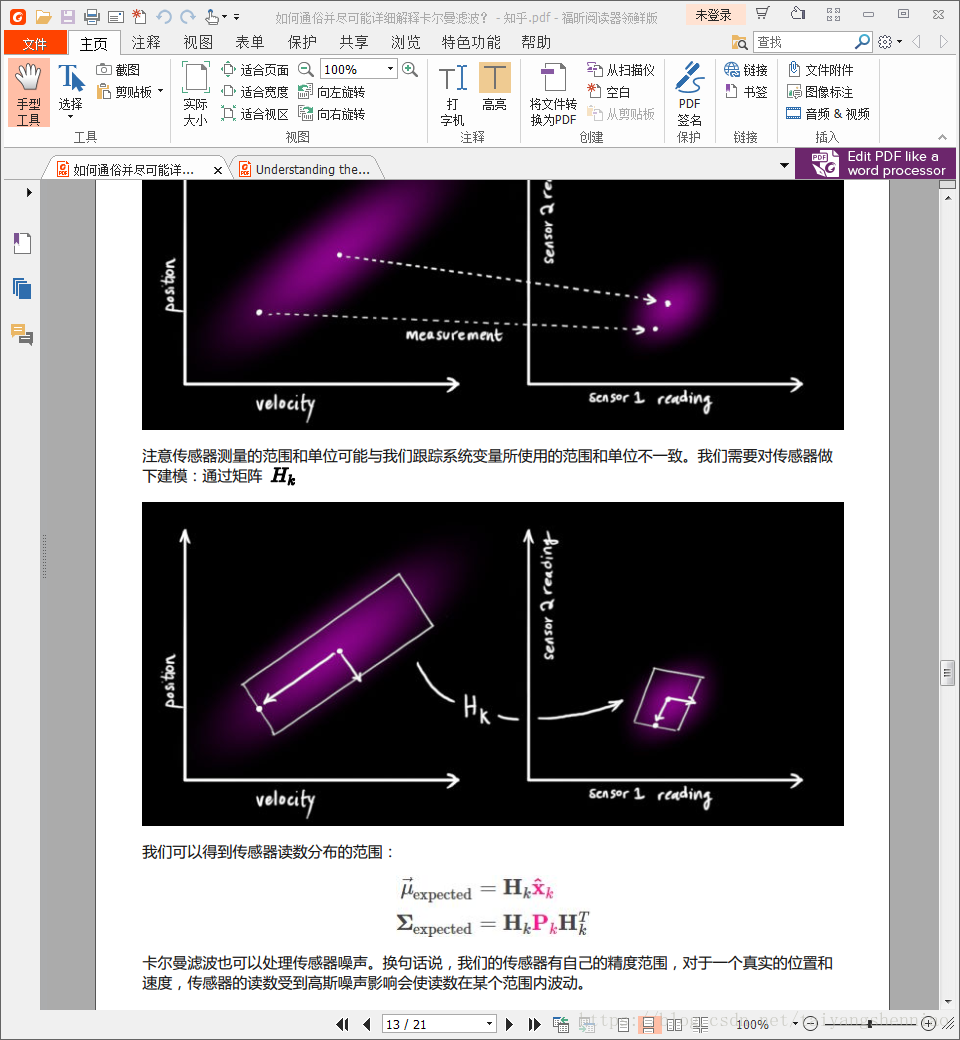
同样经过Hk变换后系统的测量的协方差矩阵也发送了变化,即
Pm=Ht*Pt*HtT
但是由于测量传感器也是存在误差的,比如雷达传感器就会存在干扰以及信噪比不够导致的测量不准确等等,我们统称测量上引入的干扰也是用方差表示,称之为:Rt,如下图所示:
所以测量系统最后得到的协方差矩阵为:Pm=Ht*Pt*HtT + Rt
其中Rt与Pm的关系与Qt和Pt的关系式一样的,注意区别。
//***************************************************************************************//
到目前为止,我们已经获得了两套目标信息,一套是通过预测得到的目标状态,以及他的协方差矩阵;另外一套就是通过实际测量得到的一套目标状态信息和他的协方差矩阵。
现在的关键问题是如何取舍,相信谁更多一点。这个比例怎么分配。如下所示:
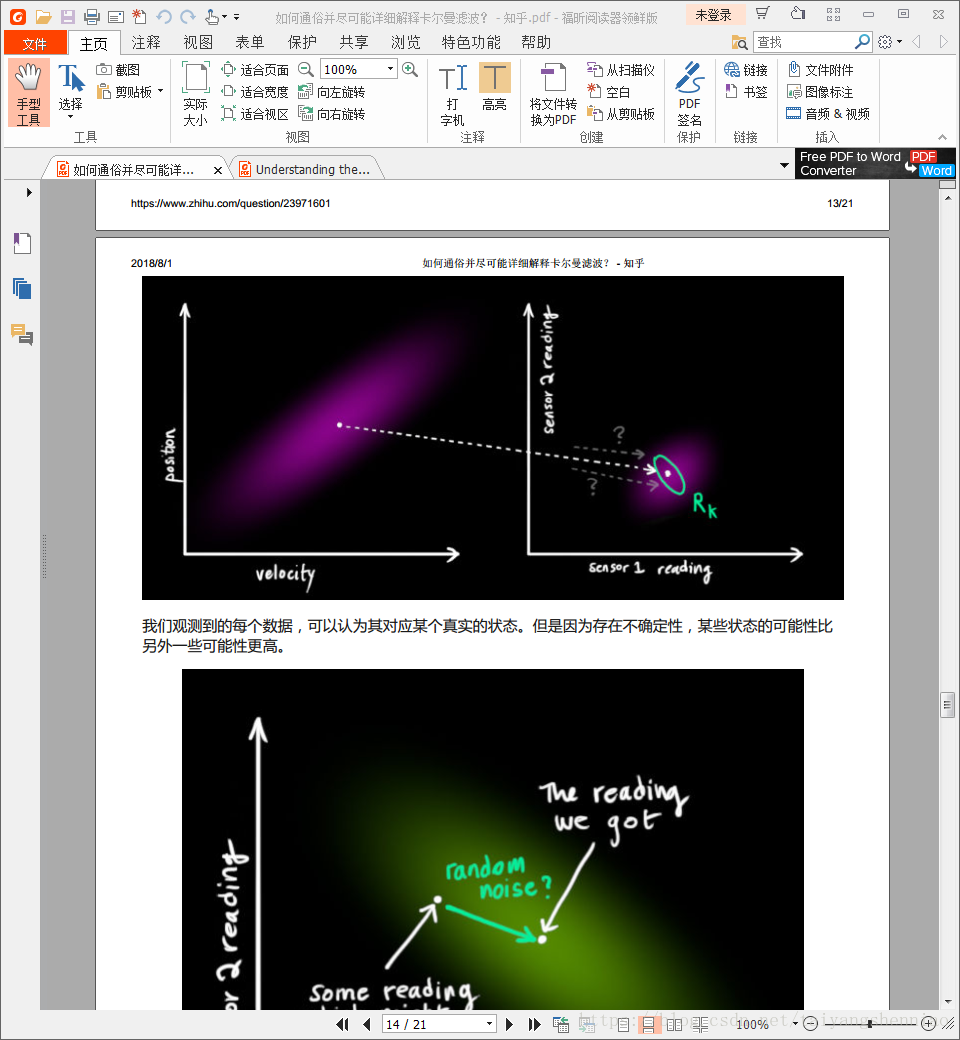
图中有两个区域位置,一个是通过预测得到,预测得到位置为黄色正太分布的期望,但是由于存在误差,所以他还有一个方差存在,即Pt
另外一个蓝色的区域,是测量得到的,同样,测量得到的状态量带变了蓝色分布的期望值,他的协方差矩阵表征了由于误差到来的变动范围。
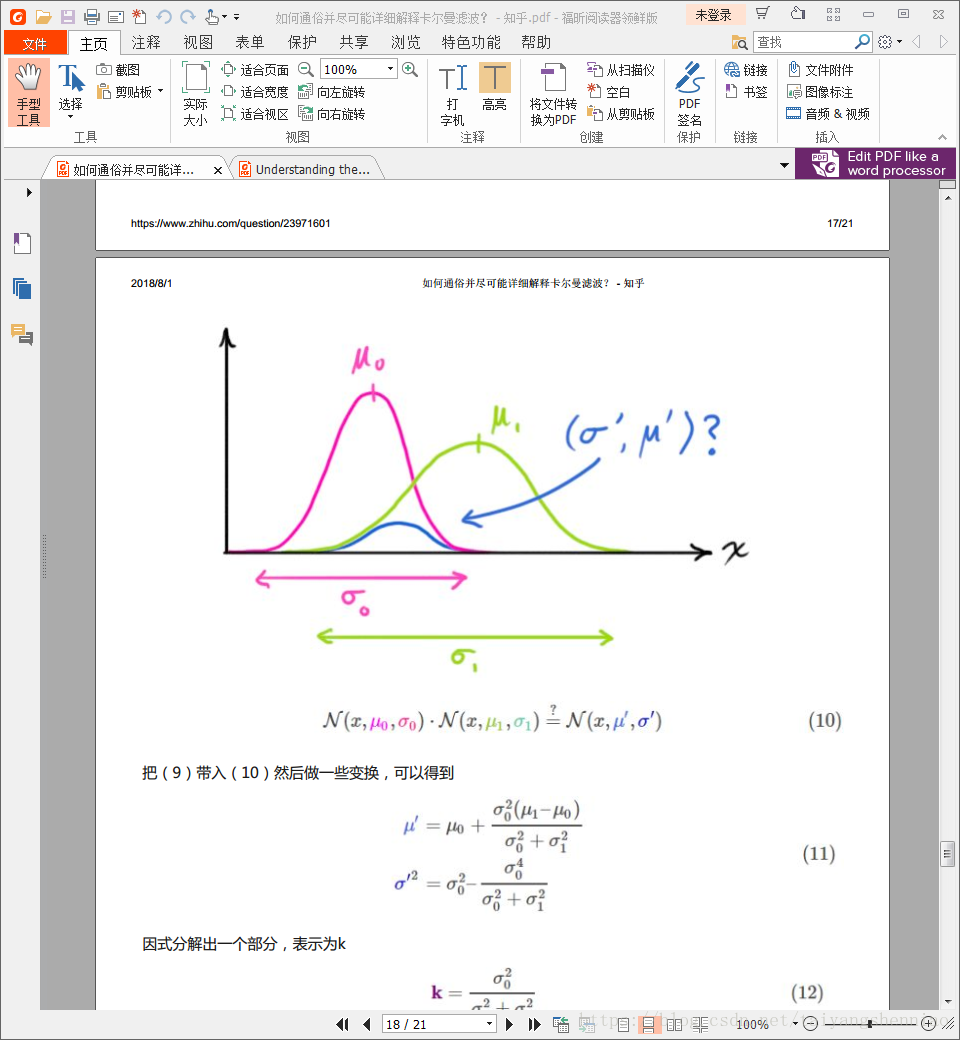
如何在这两个分布中获取最优的占比。方法是获取他们的交集。然而对于一维的正态分布,获取他们交集的一个办法就是把两个正太分布的pdf(概率密度函数)相乘即可。如下图所示:
求解得到的新的正太分布的期望值就是当前帧的状态预测值。得到的方差矩阵就会是预测后目标可能存在的一个变动范围。
下面介绍两个正太分布如何相乘。在介绍之前,先把几个变量的含义搞清楚。如上图。首先假定紫红色的正太分布图代表的是预测值得;绿色代表的是传感器测量值的。
那么相对于上一时刻而言,期望值u0就是预测得到的系统量xt|t-1
最后两个正太分布相乘之后化简得到:
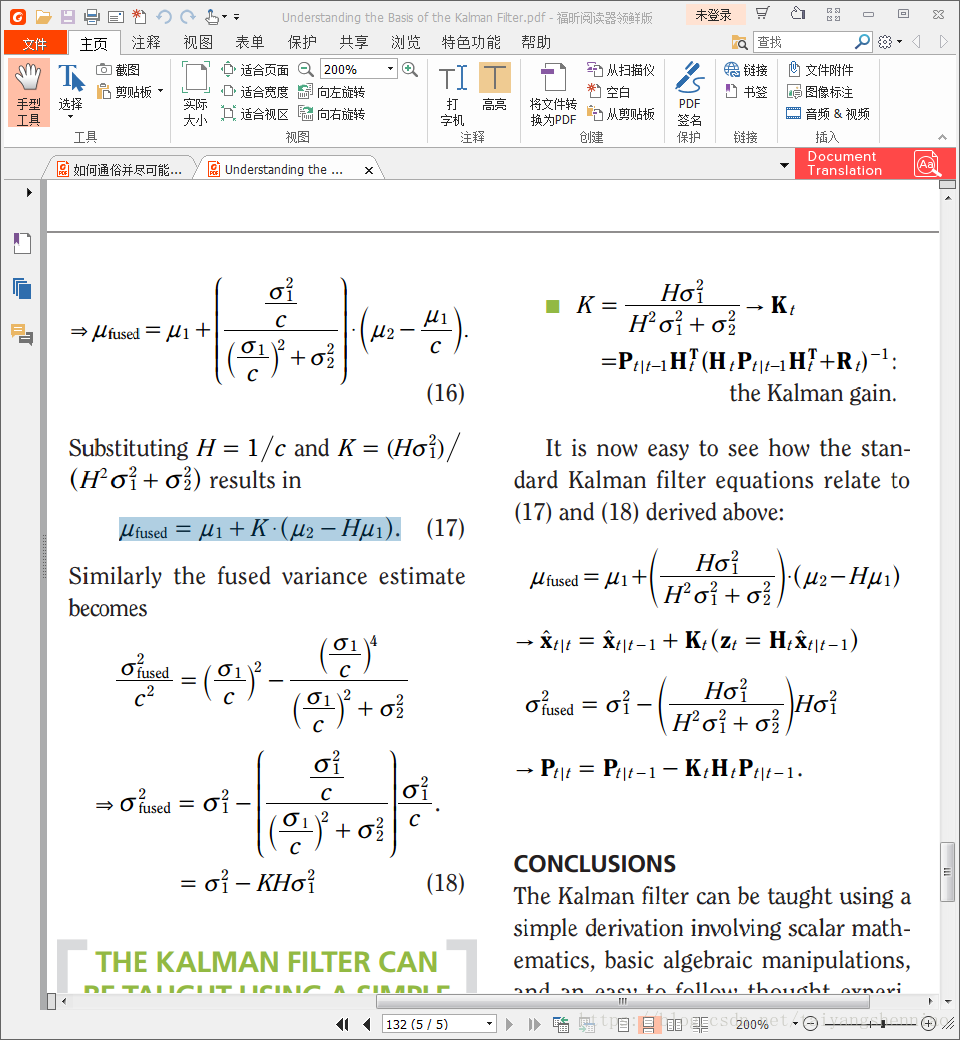
最后总结公式如下:
u'= u1+K*(u2-Hu1)
б'2= б12-KHб12
K= Hб12/(HHб12+ б22)
u0就是预测得到的系统量xt|t-1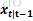
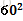

由这三个公式在加上(1)和(3)便是整个卡尔曼滤波的过程和公式的由来。
//***************************************************************************************//
下面是计算卡尔曼的过程:
这个流程中有一个问题,就是Qt和Rt如何获得,
首先对于Qt和Rt都是属于系统的误差带进来的,和系统的状态向量是无关向量,所以可以认为Qt和Rt的两个状态量是线性无关的,既然是线性无关,那么Qt和Rt就是一个对角矩阵。出对角线元素以外,其他元素都为零。
对于对角线上的值,同样假设系统的状态量为距离和速度,那么对于Qt而言,是属于系统的预测误差,这个误差主要来源是计算误差,理论上应该是较小的。但是其真实值我们是不知道的,所以可以选择对于
Qt= 0.5000.1
但是Rt则是测量误差引起的,从雷达传感器的经验上看,他的误差距离在±3m左右,速度的误差在±1.5m/s左右,所以用这个值带入得到Rt矩阵。
//***************************************************************************************//
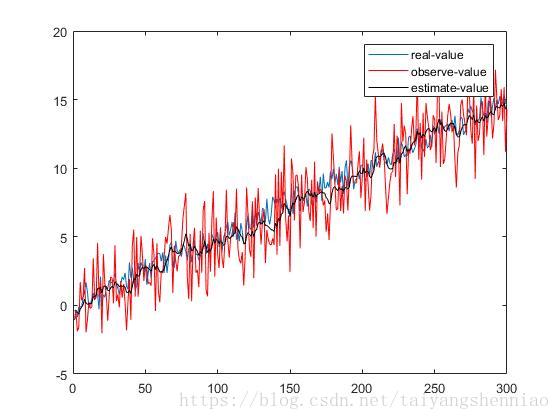
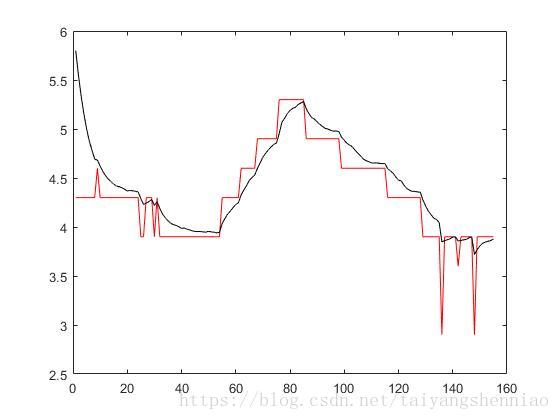
仿真和实际数据效果:
从上面两幅图中分析,蓝色代表的是带有波动的真是数据,红色是混叠了其他干扰最后测量得到的结果。卡尔曼预测通过预测值和红色的观测值,预测得到的结果为黑色线条的结果和蓝色的真是结果是十分相近的。
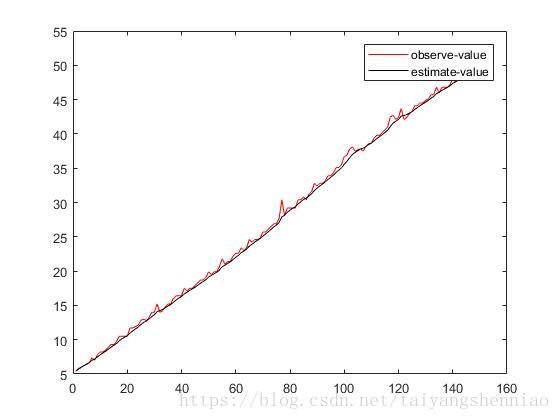
真实数据:
这是真实数据跟踪预测得到的距离和速度值。
但是这里有一个问题,就是我的Rt和Qt的协方差矩阵中的方差必须要选择的和系统真实的类似。只能通过人工手动的去选择,只有选择到和合适的才能够很好的预测下一次的位置,如果选择的不合适,就会出现卡尔曼平滑或者是预测点不收敛的情况。
//********************************************************************************************//
close all;clearvars;clc;
dbstop if error;
N = 300; %快拍数
x = zeros(1,N); %状态量1 (距离)
y = zeros(1 , N); %状态量2 (速度)
a = 1; %加速度
x(1) = 0; %初始值
y(1) = 0; %初始值
T = 0.05; %时间间隔
A = [1 T ; 0 1]; %状态转移矩阵
B = [(T*T)/2 T]'; %控制矩阵
Z = [x ; y]; %观测值
X = [x ; y]; %真实值
H = [1 0 ; 0 1]; %测量值与状态量之间的转换矩阵
%% 添加噪声 ; 此处量参数用于仿真,实际中是由系统的和测量设备的精度来决定的
W =[1 , 0.5] * (rand(2,N).*2-1) ; %由系统自带的噪声引入的噪声量,距离为±1m的误差;速度为±0.5m的误差
V = [3 , 1.5] * (rand(2,N).*2-1); %由测量系统引入的噪声量(干扰、能量等),距离为±3m的误差;速度为±1.5m的误差
%%
%产生原始数据
for k = 2: N
X(:,k) = A*X(:,k-1)+ B*a;
end
X = X + W; %添加噪声
Z = X + V; %添加噪声
%% 获取状态转移初始化协方差矩阵和观察误差协方差矩阵 ; 此处在实际使用的时候,是要根据具体来调整的。只有设定的值和系统正式方差越接近,估计效果越好
Q =0.3 ^2*eye(2); %状态转移初始化协方差矩阵
R =2.5 ^2*eye(2); %观察误差协方差矩阵
P = 1*eye(2); %初始协方差矩阵
x(1) = Z(1,1);
y(1) = Z(1,2);
Xk = [x; y;];
for k = 2:N;
Xk(:,k) = A*Xk(:,k-1) + B*a;
P = A*P*A'+Q;
Kg = P*H'/(H*P*H'+R);
Xk(:,k) = Xk(:,k) + Kg*(Z(:,k)-H*Xk(:,k));
P = P - Kg*H*P;
end
figure
plot(X(1,:));hold on;plot(Z(1,:) , '-r');hold on;plot(Xk(1,:) , '-k');
legend('real-value' , 'observe-value' , 'estimate-value');
figure
plot(X(2,:));hold on;plot(Z(2,:) , '-r');hold on;plot(Xk(2,:) , '-k');
legend('real-value' , 'observe-value' , 'estimate-value');
% var(Xk(1,:))
% var(Z(1,:))