快速傅立叶变换(FFT)算法(原来这就是蝶形变换)

为了实现FFT的海面模拟，不得不先撸个FFT算法实现。

离散傅立叶变换(DFT)

学习FFT之前，首先要先了解什么是DFT，我们都知道傅立叶变换是将时域转换为频域。但是我们计算机是没办法处理连续的点，因此就有了离散傅立叶变换DFT。

标准DFT公式：

$X(k)=\sum_{n=0}^{N-1}x(n)e^{-i^{\frac{2\pi k}{N}n}},k\in {0,1,...,N-1}$

我们令：

$W_{N}^{k}=e^{-i^{\frac{2\pi k}{N}}}$

W的一些性质

$W_{N}^{k}=W_{2N}^{2k}$

证明： $\dpi{120} W_{N}^{k}=e^{-i^{\frac{2\pi k}{N}}} =cos(- \frac{2\pi k}{N})+isin(- \frac{2\pi k}{N})$ $=cos(- \frac{2\pi (2k)}{2N})+isin(- \frac{2\pi (2k)}{2N}) =W_{2N}^{2k}$

$W_{N}^{k+\frac{N}{2}}=-W_{N}^{k}$

$W_{N}^{0}=W_{N}^{N}$

证明方法同上。

快速傅立叶变换(FFT)

我们将X(k)按照奇偶组合，在 $k\in {0,1,...,\frac{N}{2}-1}$ ，有：

$X(k)=\sum_{n=0}^{N-1}x(n)e^{-i^{\frac{2\pi k}{N}n}}$

$=\sum_{n=0}^{\frac{N}{2}-1}x(2n)e^{-i^{\frac{2\pi k}{N}(2n)}}+\sum_{n=0}^{\frac{N}{2}-1}x(2n+1)e^{-i^{\frac{2\pi k}{N}(2n+1)}}$

$=\sum_{n=0}^{\frac{N}{2}-1}x(2n)e^{-i^{\frac{2\pi k}{\frac{N}{2}}n}}+e^{-i^{\frac{2\pi k}{N}}}\sum_{n=0}^{\frac{N}{2}-1}x(2n+1)e^{-i^{\frac{2\pi k}{\frac{N}{2}}n}}$

因为 $e^{-i^{\frac{2\pi}{N}}}$ 是常数，所以X(k)可以更改为：

$X(e^{-i^{\frac{2\pi k}{N}}})=\sum_{n=0}^{N-1}x(n)e^{-i^{\frac{2\pi k}{N}n}}$

即：

$X(W_{N}^{k})=\sum_{n=0}^{N-1}x(n)(W_{N}^{k})^{n}$

$=\sum_{n=0}^{\frac{N}{2}-1}x(2n)(W_{\frac{N}{2}}^{k})^{n}+(W_{N}^{k})\sum_{n=0}^{\frac{N}{2}-1}x(2n+1)(W_{\frac{N}{2}}^{k})^{n},k\in {0,1,...,\frac{N}{2}-1}$

我们令

$F(W_{\frac{N}{2}}^{k})=\sum_{n=0}^{\frac{N}{2}-1}x(2n)(W_{\frac{N}{2}}^{k})^{n}$ ， $G(W_{\frac{N}{2}}^{k})=\sum_{n=0}^{\frac{N}{2}-1}x(2n+1)(W_{\frac{N}{2}}^{k})^{n}$

可得 $X(W_{N}^{k})$ 在 $k\in {0,1,...,\frac{N}{2}-1}$ 时，

$X(W_{N}^{k})=F(W_{\frac{N}{2}}^{k})+W_{N}^{k} G(W_{\frac{N}{2}}^{k})$

我们这里发现F，G为X的递归函数。

然后计算 $X(W_{N}^{k+\frac{N}{2}})$ ， $k\in {0,1,...,\frac{N}{2}-1}$ ：

$X(W_{N}^{k+\frac{N}{2}})=F(W_{\frac{N}{2}}^{k+\frac{N}{2}})+W_{N}^{k+\frac{N}{2}} G(W_{\frac{N}{2}}^{k+\frac{N}{2}})$

$=F(W_{N}^{2k+N})+W_{N}^{k+\frac{N}{2}} G(W_{N}^{2k+N})$

$=F(W_{N}^{2k}W_{N}^{N})-W_{N}^{k} G(W_{N}^{2k}W_{N}^{N})$

$=F(W_{\frac{N}{2}}^{k})-W_{N}^{k} G(W_{\frac{N}{2}}^{k})$

根据以上公式： $X(W_{N}^{k})=F(W_{\frac{N}{2}}^{k})+W_{N}^{k} G(W_{\frac{N}{2}}^{k})$ ， $X(W_{N}^{k+\frac{N}{2}})=F(W_{\frac{N}{2}}^{k})-W_{N}^{k} G(W_{\frac{N}{2}}^{k})$

我们发现想要求 $X(W_{N}^{k})$ 与 $X(W_{N}^{k+\frac{N}{2}})$ ，只需要要求出 $F(W_{\frac{N}{2}}^{k})$ 与 $G(W_{\frac{N}{2}}^{k})$ 就可以了，这两条公式也就是我们所说的蝶形运算式。

我们令N=4，这时候出现了一幅熟悉的图，4-point FFT蝴蝶变换图：

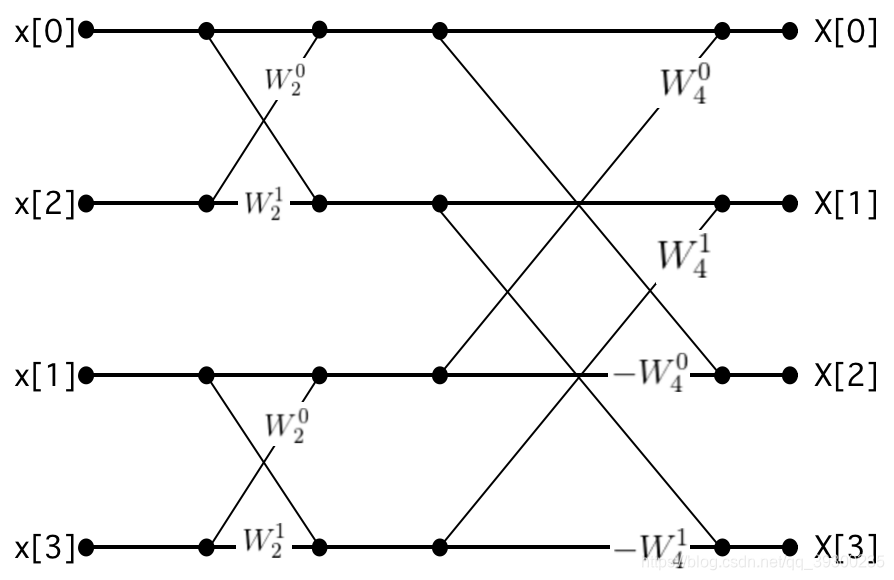
说实话，我第一次看这个看了半天没看懂，就像瞎比划出来的东西，然而，我们只要举个例子就明白了：

我们首先计算k=0的情况：

$X(W_{4}^{0})=F(W_{2}^{0})+W_{4}^{0}G(W_{2}^{0})=\sum_{n=0}^{1}x(2n)(W_{2}^{0})^{n}+W_{4}^{0}\sum_{n=0}^{1}x(2n+1)(W_{2}^{0})^{n}$

$F(W_{2}^{0})=F_{f}(W_{1}^{0})+W_{2}^{0}G_{f}(W_{1}^{0})$

$=\sum_{n=0}^{0}x(4n)(W_{1}^{0})^{n}+W_{2}^{0}\sum_{n=0}^{0}x(4n+2)(W_{1}^{0})^{n}$

$=x(0)+x(2)W_{2}^{0}$

$G(W_{2}^{0})=F_{g}(W_{1}^{0})+W_{2}^{0}G_{g}(W_{1}^{0})$

$=\sum_{n=0}^{0}x(4n+1)(W_{1}^{0})^{n}+W_{2}^{0}\sum_{n=0}^{0}x(4n+3)(W_{1}^{0})^{n}$

$=x(1)+x(3)W_{2}^{0}$

其中 $F_{f}$ ， $G_{f}$ 为F的递归函数。 $F_{g}$ ， $G_{g}$ 为G的递归函数。

所以我们的 $X(W_{4}^{0})$ 为：

$X(W_{4}^{0})=x(0)+x(2)W_{2}^{0}+W_{4}^{0}(x(1)+x(3)W_{2}^{0})$

首先公式：

$X(W_{4}^{0})=F(W_{2}^{0})+W_{4}^{0}G(W_{2}^{0})$ ，

过程如下图所示(其中 $X[ i]=X(W_{4}^{i})$ )：

下面两条公式：

$F(W_{2}^{0})=F_{f}(W_{1}^{0})+W_{2}^{0}G_{f}(W_{1}^{0})=x(0)+x(2)W_{2}^{0}$ ，

$G(W_{2}^{0})=F_{g}(W_{1}^{0})+W_{2}^{0}G_{g}(W_{1}^{0})=x(1)+x(3)W_{2}^{0}$

图解为：

由于我们求出 $F(W_{\frac{N}{2}}^{k})$ 与 $G(W_{\frac{N}{2}}^{k})$ 也能求出 $X(W_{N}^{k+\frac{N}{2}})$ 的值，其完成的图为：

到这里，就是我们标准的傅立叶变换了，我们的算法复杂度从 $O(N^{2})$ 变成了 $O(Nlog_{2}N)$ 。

bitreverse算法

然而，我们的FFT还可以使用非递归的版本，如我们的4-point FFT计算X[0],X[1],X[2],X[3]最后对应的输入为x[0],x[2],x[1],x[3]。

再看8-point FFT计算过程x的位置变化：

0 1 2 3 4 5 6 7

0 2 4 6 1 3 5 7

0 4 2 6 1 5 3 7

bitreverse算法则是从中发现了x[i]在几号位，只要将i转化为 $log_{2}N$ (N-point FFT)位二进制，然后将bit反序再转回10进制即可，所得的数就是在第几位。比如在8-point FFT中我们想知道x(4)在几号位，我们只要将2转化为 $log_{2}8=3$ 位二进制100，然后反序得001，即10进制的1。所以x(4)最后的位置为1号位(从0开始)。

所以我们的FFT便可以写成迭代的版本了(即上面蝶形变换图从左往右推)。贴上代码：

//其中a为x[i],omg为WNk
void fft(cp *a, cp *omg){
    int lim = 0;
    while((1 << lim) < n) lim++;//logN 

    //二进制反序
    for(int i = 0; i < n; i++){
        int t = 0;
        for(int j = 0; j < lim; j++)
            //每当该位上的值为1时，t和该位反转后的值进行或运算
            if((i >> j) & 1) t |= (1 << (lim - j - 1));
        if(i < t) swap(a[i], a[t]); // i < t 的限制使得每对点只被交换一次
    }
    
    //FFT计算
    for(int l = 2; l <= n; l *= 2){
        int m = l / 2;
        for(cp *p = a; p != a + n; p += l)
            for(int i = 0; i < m; i++){
                //蝶形变换
                cp t = omg[n / l * i] * p[i + m];
                p[i + m] = p[i] - t;
                p[i] += t;
            }
    }
}

其中FFT计算的第一层循环为下图所示分块计算：