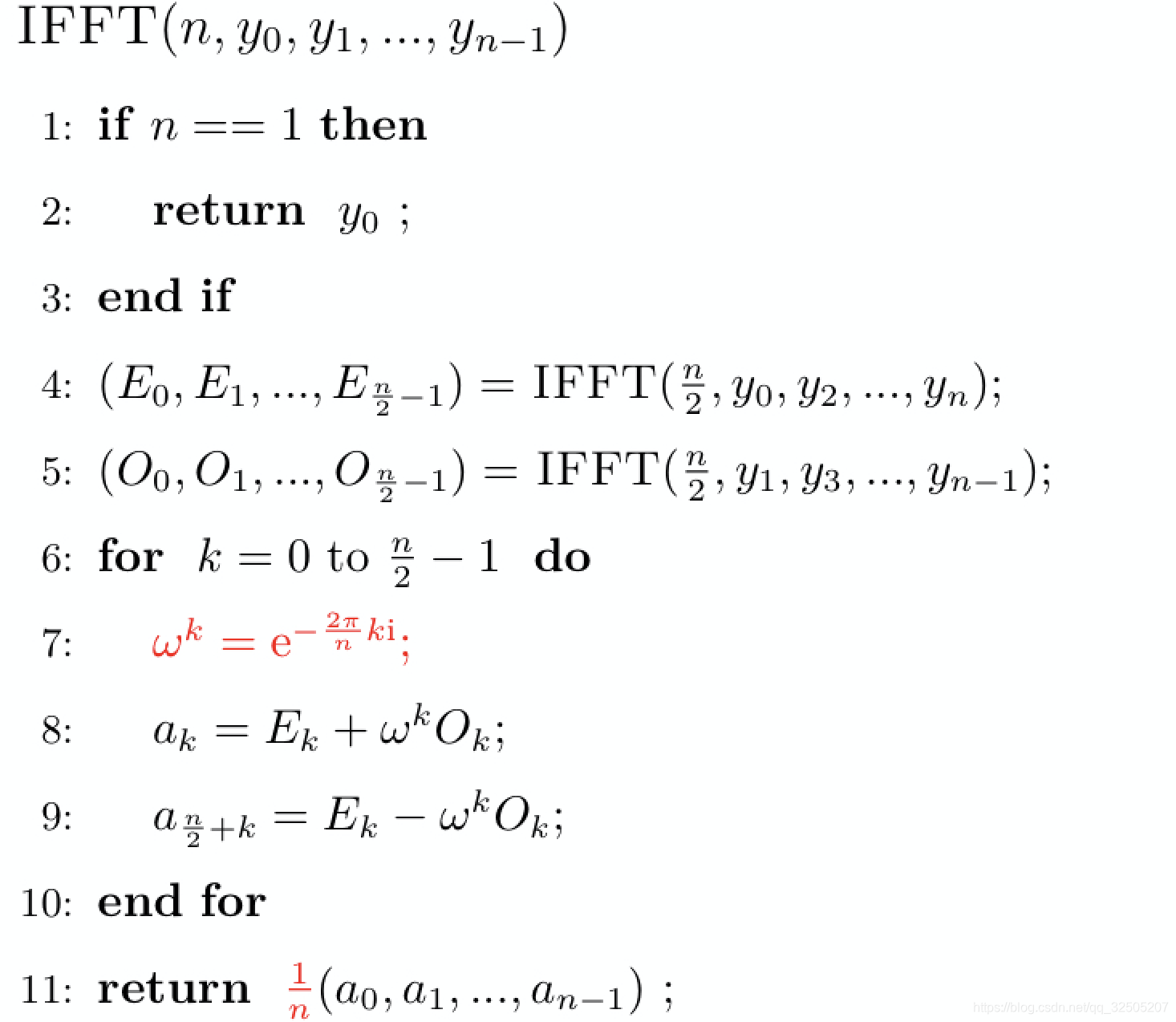引言
DFT:离散傅立叶变换,求一个多项式在n个特殊点的值;
FFT:DFT的改进的快速实现
常见应用:两个多项式相乘(和两个n位整数相乘);时频变换;求解偏微分方程;
FFT中运用了分治的思想
问题描述
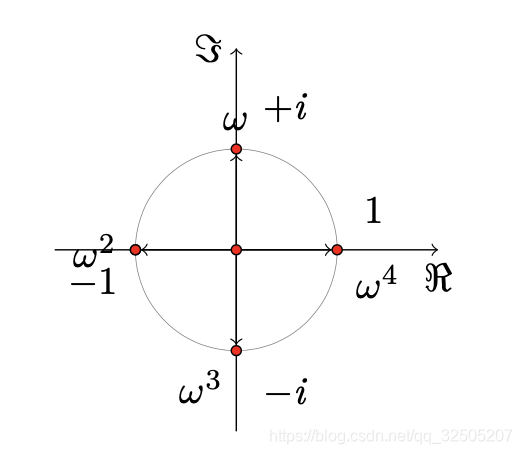
给定一个多项式 A ( x ) = a 0 + a 1 x + . . . + a n − 1 x n − 1 A(x) = a_0+a_1x+...+a_{n-1}x^{n-1} A(x)=a0+a1x+...+an−1xn−1,求其在给定的点: 1 , ω , ω 2 , . . . , ω n − 1 1,\omega,\omega^2,...,\omega^{n-1} 1,ω,ω2,...,ωn−1的值,其中 ω = e 2 π n i \omega=e^{\frac{2\pi}{n}i} ω=en2πi。如下图所示,也就是求解y。

如果我们用最简单的因式分解的算法,则需要进行(n-1)次加法和乘法操作,则复杂度为 O ( n 2 ) O(n^2) O(n2)。
A ( x ) = a 0 + x ( a 1 + x ( a 2 + . . . + a n − 1 x n − 1 ) A(x) = a_0+x(a_1+x(a_2+...+a_{n-1}x^{n-1}) A(x)=a0+x(a1+x(a2+...+an−1xn−1)
解决思路
实际上我们通过推算可以发现有好多冗余的计算,我们可以通过分治思想来减少冗余计算。
多项式能进行分治的前提,是因为单位复根的周期性变化, e π = − i , e 2 π = i e^{\pi}=-i,e^{2\pi}=i eπ=−i,e2π=i,所以 ω i = w n + i \omega^i=w^{n+i} ωi=wn+i。
举几个例子
当n=4时,我们把展开式的 a 1 a_1 a1列和 a 2 a_2 a2列交换一下,如下图所示,我们可以发现阴影部分出现了冗余计算,前面两列一模一样,后面两列上下对比只是多乘了 w 2 w^2 w2。因此我们只需要计算一半的内容即可。由于加法次数多于乘法,因此复杂度只需考虑加法使用的次数,本次计算需要:2(左) + 2(右) + 4(中间)= 4 l o g 2 4 4log_24 4log24 次加法。
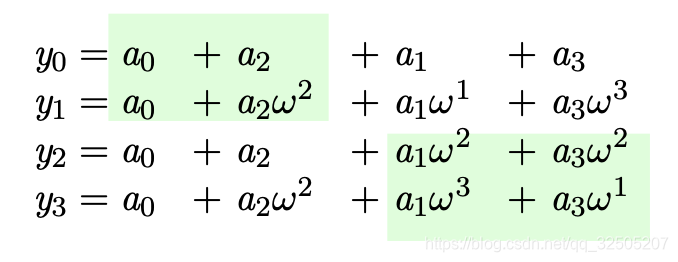
当n=8时,展开式如下
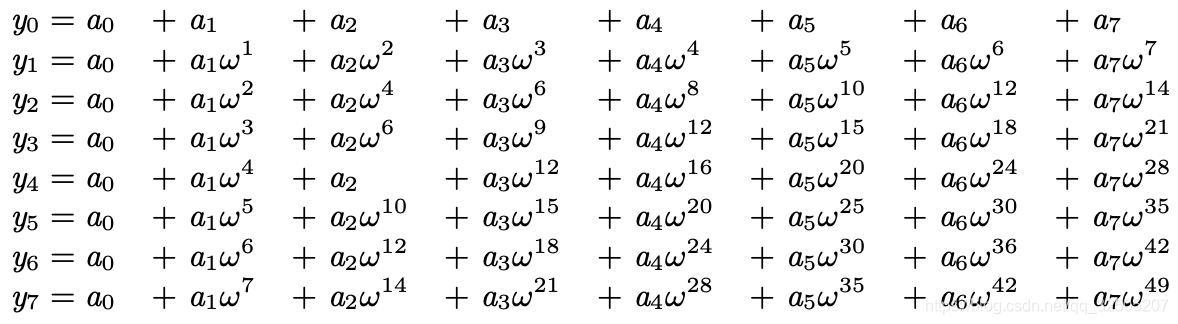
根据周期化简之后的展开式,再经过换一下奇偶列的位置,我们同样可以看到存在冗余计算,我们现在就发现了使用分治的划分规则:下标的奇偶性。每次递归分治划分后,偶数部分一样,只需要计算一遍加法,奇数部分要乘上 ω i ω^i ωi再计算加法。
n=8,我们需要进行 2 + 4 + 2 + 8 + 2 + 4 + 2 = 8 × l o g 2 8 2 + 4 + 2 + 8 + 2 + 4 + 2 = 8 × log_2 8 2+4+2+8+2+4+2=8×log28次加法
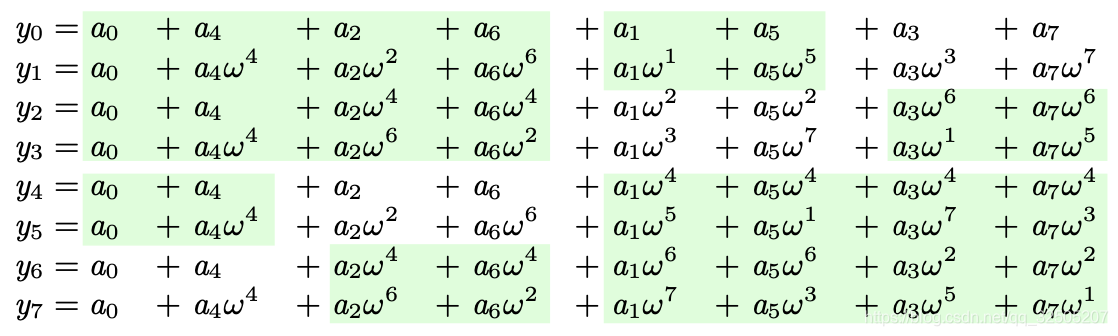
我们可以算出此问题的复杂度为:
T ( n ) = 2 T ( n 2 ) + O ( n ) = O ( n l o g 2 n ) T(n) = 2T(\frac{n}{2})+O(n) = O(n log_2 n) T(n)=2T(2n)+O(n)=O(nlog2n)
伪代码如下
E是计算偶数下标,O是计算奇数下标
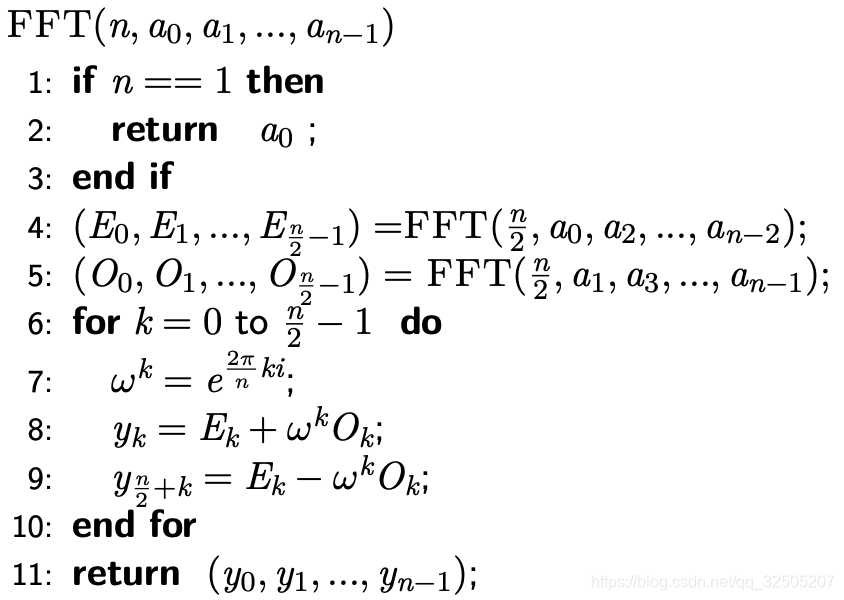
逆快速傅立叶变换(IFFT)
逆快速傅立叶变换就是傅立叶变换的反过程,即已知特定的点和特定点的值y,求多项式系数a。
IFFT:本身是一个求逆的过程,由于范德蒙矩阵的特性,得到结果如下, ω ‾ \overline{\omega} ω表示共轭
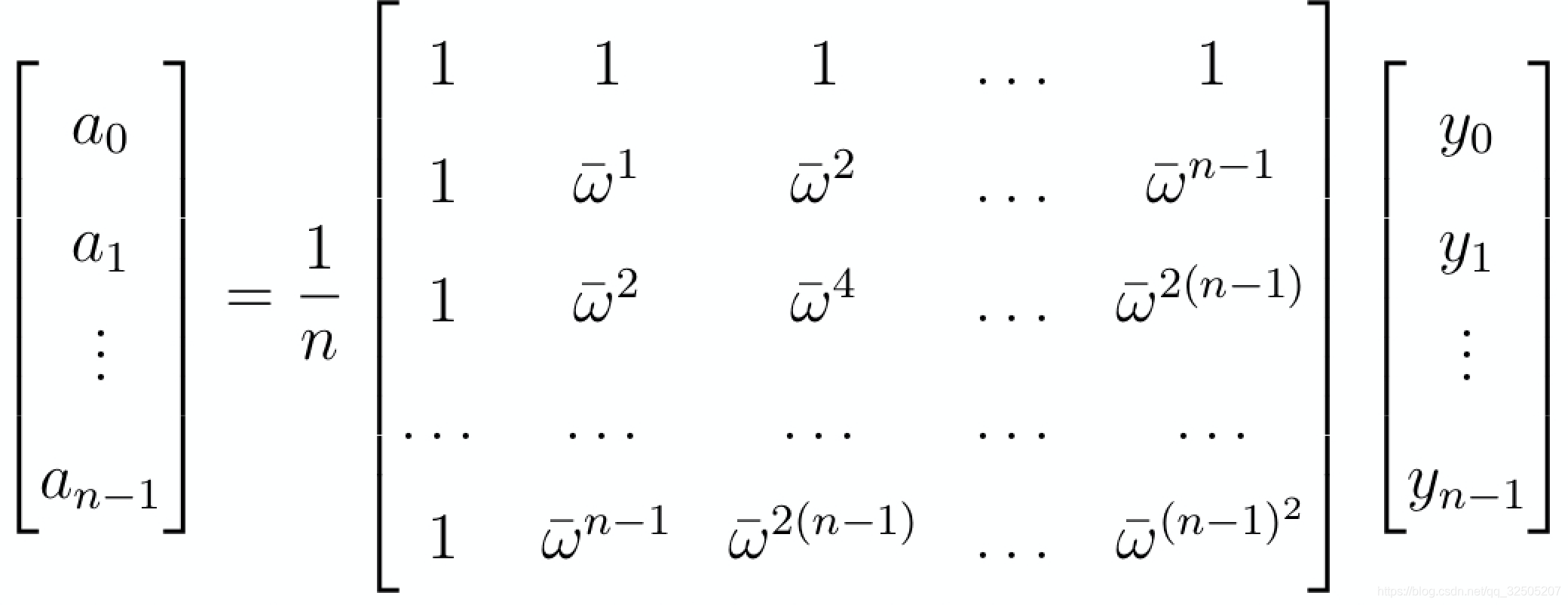
FFT

伪代码只需在FFT之上做些许变动即可,如下: