转自大佬博客https://www.cnblogs.com/zhouzhendong/
原文链接https://www.cnblogs.com/zhouzhendong/p/Fast-Fourier-Transform.html
如果禁止转载请联系我
留待学习傅立叶和ntt
多项式 之 快速傅里叶变换(FFT)/数论变换(NTT)/例题与常用套路【入门】
前置技能
- 对复数以及复平面有一定的了解
- 对数论要求了解:逆元,原根,中国剩余定理
- 对分治有充足的认识
- 对多项式有一定的认识,并会写 O(n2)O(n2) 的高精度乘法
本文概要
- 多项式定义及基本卷积形式
- KaratsubaKaratsuba 乘法
- 多项式的系数表示与点值表示,以及拉格朗日插值法
- 复数与单位根
- 快速傅里叶变换 (FFT)(FFT)
- 数论变换 (NTT)(NTT)
- 分治 FFTFFT
- 拆系数 FFTFFT 和三模数 NTTNTT
- 例题与套路
前言
近年来,多项式理论进入中国,在中国 OIOI 界逐渐占据一方,是一个值得我们去研究的理论。现在, OIOI 题中出现次数越来越频繁的多项式题,也鼓励了许多 OIerOIer 去学习多项式。
作为多项式的一个重要算法—— FFTFFT ,它有着极其优越的作用。比如,对于初学高精度时的你,是否听说过高精度乘法可以 O(nlogn)O(nlogn) ? FFTFFT 可以来解决一类多项式卷积,顺便秒掉了高精度乘法。
于是,菜鸡博主去学了一下 FFTFFT ,写了这篇总结。
多项式定义及基本卷积形式
多项式
定义 多项式 为形如下式的代数表达式。
P(x)=∑i=0naixi=a0+a1x+a2x2+⋯+anxnP(x)=∑i=0naixi=a0+a1x+a2x2+⋯+anxn
其中 a0,a1,a2,⋯,ana0,a1,a2,⋯,an 称为多项式的 系数。
xx 没有确定的值。
最高次项的指数 nn 叫做多项式的 度 (Degree,n=deg P)(Degree,n=deg P) ,也可以说是多项式的 次数。
多项式基本卷积形式
下面的这个多项式卷积就是多项式乘法。
定义两个多项式 g(x),f(x)g(x),f(x) ,设他们的度数分别为 n,mn,m ,则卷积具有如下形式:(设 gigi 为 gg 的 ii 次项系数, fifi 为 ff 的 ii 次项系数)
h(x)=g(x)f(x)=∑i=0n∑j=0mgifjxi+jh(x)=g(x)f(x)=∑i=0n∑j=0mgifjxi+j
=∑i=0n+m∑j=0igjfj−ixi=∑i=0n+m∑j=0igjfj−ixi
请务必理解并记住第二行的卷积式,这将会在后面不停的出现。
我们显然可以通过公式来 O(nm)O(nm) 得到卷积结果。
KaratsubaKaratsuba 乘法
针对这种卷积, KaratsubaKaratsuba 提出了下面的这种方法:
对于多项式 FF ,我们令 n=deg F+1n=deg F+1 。
即多项式可以写成这个形式: F(x)=∑n−1i=0aixiF(x)=∑i=0n−1aixi 。
令 F(x)=F0(x)+xn2F1(x),G(x)=G0(x)+xn2G1(x)F(x)=F0(x)+xn2F1(x),G(x)=G0(x)+xn2G1(x) 。
其中, deg F0=deg F1=deg G0=deg G1=n2deg F0=deg F1=deg G0=deg G1=n2 。
则
(F×G)(x)=(F0×G0)(x)+xn2(F0×G1+F1×G0)(x)+xn(F1×G1)(x)(F×G)(x)=(F0×G0)(x)+xn2(F0×G1+F1×G0)(x)+xn(F1×G1)(x)
令 M(x)=((F0+F1)×(G0+G1))(x)M(x)=((F0+F1)×(G0+G1))(x)
我们会开心的发现:
(F0×G1+F1×G0)(x)=M(x)−(F0×G0)(x)−(F1×G1)(x)(F0×G1+F1×G0)(x)=M(x)−(F0×G0)(x)−(F1×G1)(x)
于是我们只需要计算三个多项式卷积 M(x),(F0×G0)(x)−(F1×G1)(x)M(x),(F0×G0)(x)−(F1×G1)(x) 即可。
我们采用分治的做法,于是时间复杂度为:
T(n)=3T(n2)+O(n)=nlog23≈n1.585T(n)=3T(n2)+O(n)=nlog23≈n1.585
多项式的系数表示与点值表示,以及拉格朗日插值法
系数表示
(令 n=deg Fn=deg F )
这里拿出了最开始提到的多项式:
f(x)=a0+a1x+a2x2+⋯+anxnf(x)=a0+a1x+a2x2+⋯+anxn
把 aa 数组看作 n+1n+1 维向量 a⃗ =(a0,a1,⋯,an)a→=(a0,a1,⋯,an) ,其 系数表示 就是向量 a⃗ a→ 。
点值表示
(令 n=deg Fn=deg F )
取任意 n+1n+1 个不同的 x0,x1,⋯,xnx0,x1,⋯,xn 代入多项式进行求值,得到了 n+1n+1个不同的二元组 (x0,F(x0)),(x1,F(x1)),⋯,(xn,F(xn))(x0,F(x0)),(x1,F(x1)),⋯,(xn,F(xn)) 。
我们称这 n+1n+1 个点表示多项式的方法叫做多项式的 点值表示 。
这里要注意,多项式的点值表示有无数种,但是多项式的系数表示是唯一的。
拉格朗日插值法
实现系数表示到点值表示的变换,我们可以直接把 xx 代入求解,复杂度 O(n2)O(n2) 。
但是点值表示转系数表示就没这么简单了。
这里首先提一点:虽然同一个多项式的点值表示有无数种,但是这些点值表示都能唯一的确定一个多项式,唯一的确定一个系数表示。
从点值表示转到系数表示,我们可以使用插值法。
其中拉格朗日插值法能够在 O(n2)O(n2) 的复杂度内得到系数表示。
具体在这里不展开介绍了,可以参见:
https://www.zhihu.com/question/58333118/answer/262507694
复数与单位根
复数的定义
复数 (Complex)(Complex) 由实部和虚部组成。
可以写成如下形式:
A=a+ib,(a,b∈R,A∈C)A=a+ib,(a,b∈R,A∈C)
其中 AA 就是一个复数。
其中 i=−1−−−√i=−1 ,为虚数单位。
在后面的公式中要注意区分虚数单位 ii 和求和指标 (∑∑) ii 。
显然这里可以列举三个 FFTFFT 常用的复数运算:
(A1,A2∈C,a1,b1,a2,b2∈R)(A1,A2∈C,a1,b1,a2,b2∈R)
A1+A2=(a1+ib1)+(a2+ib2)=(a1+a2)+i(b1+b2)A1+A2=(a1+ib1)+(a2+ib2)=(a1+a2)+i(b1+b2)
A1−A2=(a1+ib1)−(a2+ib2)=(a1−a2)+i(b1−b2)A1−A2=(a1+ib1)−(a2+ib2)=(a1−a2)+i(b1−b2)
A1×A2=(a1+ib1)(a2+ib2)=a1a2+i2b1b2+ia1b2+ia2b1=(a1a2−b1b2)+i(a1b2+a2b1)A1×A2=(a1+ib1)(a2+ib2)=a1a2+i2b1b2+ia1b2+ia2b1=(a1a2−b1b2)+i(a1b2+a2b1)
复平面
复平面是个二维平面,其中横轴代表实数,称为实轴。纵轴代表虚数,称为虚轴。
定义复平面上从原点出发的向量a⃗ =(a,b)a→=(a,b)表示虚数a+iba+ib。
例如:
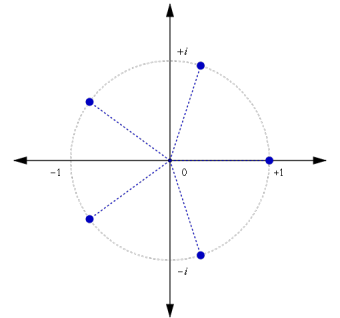
其中的 55 条蓝色向量就代表了 55 个虚数。
关于复数乘法,有一个口诀:模长相乘,幅角相加。
模长就是复数在复平面上表示的向量的模长,幅角就是以正实轴为始边,这个向量为终边所构成的角。
单位根
nn 次单位根 ωn∈Cωn∈C ,满足 ωnn=1ωnn=1 。
显然 nn 次方程有 nn 个解,把他们写在复平面上面,可以把单位圆等分成 nn份。由于复数乘法模长相乘,所以模长永远是 11 ,说明他们总在单位圆上。由于幅角相加,得到他们等分单位圆。
于是我们可以写出单位根的表达式:
记 ωn=cos(2πn)+isin(2πn)ωn=cos(2πn)+isin(2πn) ,则 nn 次单位根就是 ω0n,ω1n,⋯,ωn−1nωn0,ωn1,⋯,ωnn−1 。
通项公式, ωin=cos(2iπn)+isin(2iπn) (0≤i<n)ωni=cos(2iπn)+isin(2iπn) (0≤i<n)
当然,在数学上,单位根还有这种定义: ωn=e2πinωn=e2πin ,读者可以尝试通过这个来推导前几个式子,这里不展开介绍。
单位根有一些优秀的性质。
定理1:相消定理
对于任意整数 n≥0,k≥0,d≥0n≥0,k≥0,d≥0 ,有:
ωdkdn=e2πdkidn=e2πkin=ωknωdndk=e2πdkidn=e2πkin=ωnk
即:
ωdkdn=ωknωdndk=ωnk
定理2:折半定理
对于任意的偶数 n≥0,k≥0n≥0,k≥0 ,有
ωkn=ωk2n2ωnk=ωn2k2
这个由定理1显然可得。
此外,我们还可以从复平面图像的角度理解单位根。

观察任何一个单位根 ωinωni ,
ωi+1n=ωin×ω1nωni+1=ωni×ωn1
观察其图像,会发现 ×ω1n×ωn1 的效果就是把原复数在复平面上的向量绕原点逆时针旋转2πn2πn的角度。
类似的, ×ω1n×ωn1 的效果相反,为顺时针方向。
再有,显然, ω−in=ωn−inωn−i=ωnn−i 。
于是对于整数 ii ,如果从 ω0nωn0 逆时针旋转一定角度得到的向量为单位根 ωinωni ,那么顺时针旋转相同的角度也必然会得到 ω−in=ωn−inωn−i=ωnn−i 。
于是如果把所有 nn 次单位根在复平面上画出来,他们是上下对称的。
性质3
所以如果令 ωkn=a+ibωnk=a+ib ,则 ω−kn=a−ib (a,b∈R,a2+b2−−−−−−√=1)ωn−k=a−ib (a,b∈R,a2+b2=1),即 ω−kn=conj(ωkn)ωn−k=conj(ωnk) 。
考虑到 ωnnωnn 是绕着原点转了一圈,那么 ωn2nωnn2 就是转了半圈,所以 ωn2n=−1ωnn2=−1。
所以 ωinωni 与 ωi+n2nωni+n2 在单位圆上的位置是相对的,因为转了半圈。换句话说:
性质4
ωi+n2n=ωn2n⋅ωin=−ωinωni+n2=ωnn2⋅ωni=−ωni
快速傅里叶变换(Fast Fourier Transform, FFT)
回忆一下之前的多项式卷积:
h(x)=∑i=0n+m∑j=0igjfj−ixih(x)=∑i=0n+m∑j=0igjfj−ixi
我们要快速求 h(x)h(x) 的每一项系数。
系数表示并不能支持快速的卷积。
但是在点值表示下,却可以在 O(n)O(n) 复杂度内快速卷积。
目前的瓶颈在于系数表示与点值表示的快速的相互转化。
由于点值表示有很多种,只要你选择的 xx 互不相同即可。于是我们可以考虑选择一些特殊的 xx 。
注意,后面为了方便,设多项式的度为 n−1,(n=2a,a∈Z)n−1,(n=2a,a∈Z) ,如果次数不足则高位补上系数 00 ,保证任何运算过程中多项式的真的度都小于 nn 。
离散傅里叶变换
设有多项式
F(x)=∑i=0n−1aixiF(x)=∑i=0n−1aixi
将 nn 个不同的 nn 次单位根 ω0n,ω1n,⋯,ωn−1nωn0,ωn1,⋯,ωnn−1 代入到 F(x)F(x) 中,得到点值表达式:
y⃗ =(F(ω0n),F(ω1n),⋯,F(ωn−1n))y→=(F(ωn0),F(ωn1),⋯,F(ωnn−1))
于是点值向量 y⃗ y→ 就叫做系数向量 a⃗ =(a0,a1,⋯,an−1)a→=(a0,a1,⋯,an−1) 的离散傅里叶变换 (Discrete Fourier Transform, DFT)(Discrete Fourier Transform, DFT) 。
但是直接代入求值是 O(n2)O(n2) 的,我们需要一个更快的求值方法。
令 F0(x)=∑n2−1i=0a2ixi,F1(x)=∑n2−1i=0a2i+1xiF0(x)=∑i=0n2−1a2ixi,F1(x)=∑i=0n2−1a2i+1xi
则:(下面的推导会用到之前介绍过的单位根性质的第2条和第4条)
F(x)=F0(x2)+xF1(x2)F(x)=F0(x2)+xF1(x2)
F(ωin)=F0(ω2in)+ωinF1(ω2in)=F0(ωin2)+ωinF1(ωin2)F(ωni)=F0(ωn2i)+ωniF1(ωn2i)=F0(ωn2i)+ωniF1(ωn2i)
F(ωi+n2n)=F(−ωin)=F0(ω2in)−ωinF1(ω2in)=F0(ωin2)−ωinF1(ωin2)F(ωni+n2)=F(−ωni)=F0(ωn2i)−ωniF1(ωn2i)=F0(ωn2i)−ωniF1(ωn2i)
注意: deg F0=deg F1=n2deg F0=deg F1=n2 。
于是我们可以继续分治,对于 F0F0 和 F1F1 再继续同样的操作。
时间复杂度:
T(n)=2T(n2)+O(n)=O(nlogn)T(n)=2T(n2)+O(n)=O(nlogn)
逆离散傅里叶变换
现在你需要快速的把点值表达式转换成系数表达式。
与刚才的离散傅里叶变换相反,系数向量 a⃗ =(a0,a1,⋯,an−1)a→=(a0,a1,⋯,an−1) 就叫做点值向量 y⃗ y→ 的逆离散傅里叶变换 (Inverse Discrete Fourier Transform, IDFT)(Inverse Discrete Fourier Transform, IDFT)
首先,我们把刚才的 DFTDFT 过程用矩阵来表示:
⎡⎣⎢⎢⎢⎢⎢(ω0n)0(ω1n)0⋮(ωn−1n)0(ω0n)1(ω1n)1⋮(ωn−1n)1⋯⋯⋱⋯(ω0n)n−1(ω1n)n−1⋮(ωn−1n)n−1⎤⎦⎥⎥⎥⎥⎥⎡⎣⎢⎢⎢⎢a0a1⋮an−1⎤⎦⎥⎥⎥⎥=⎡⎣⎢⎢⎢⎢⎢A(ω0n)A(ω1n)⋮A(ωn−1n)⎤⎦⎥⎥⎥⎥⎥(1)(1)[(ωn0)0(ωn0)1⋯(ωn0)n−1(ωn1)0(ωn1)1⋯(ωn1)n−1⋮⋮⋱⋮(ωnn−1)0(ωnn−1)1⋯(ωnn−1)n−1][a0a1⋮an−1]=[A(ωn0)A(ωn1)⋮A(ωnn−1)]
我们记左侧的系数矩阵为 VV ,构造矩阵 di,j=(ω−in)jdi,j=(ωn−i)j
D=⎡⎣⎢⎢⎢⎢⎢⎢(ω−0n)0(ω−1n)0⋮(ω−(n−1)n)0(ω−0n)1(ω−1n)1⋮(ω−(n−1)n)1⋯⋯⋱⋯(ω−0n)n−1(ω−1n)n−1⋮(ω−(n−1)n)n−1⎤⎦⎥⎥⎥⎥⎥⎥D=[(ωn−0)0(ωn−0)1⋯(ωn−0)n−1(ωn−1)0(ωn−1)1⋯(ωn−1)n−1⋮⋮⋱⋮(ωn−(n−1))0(ωn−(n−1))1⋯(ωn−(n−1))n−1]
设 E=D⋅VE=D⋅V ,则:
eij====∑k=0n−1dikvkj∑k=0n−1ω−iknωkjn∑k=0n−1ωk(j−i)n{n∑n−1k=0(ωj−in)k=1−(ωj−in)n1−ωj−in=0(i=j)(i≠j)eij=∑k=0n−1dikvkj=∑k=0n−1ωn−ikωnkj=∑k=0n−1ωnk(j−i)={n(i=j)∑k=0n−1(ωnj−i)k=1−(ωnj−i)n1−ωnj−i=0(i≠j)
于是我们发现了一个非常特殊的性质:
EE 是单位矩阵的 nn 倍。
也就是 1nD=V−11nD=V−1 。
于是我们将 1nD1nD 在 (1)(1) 式两侧左乘,得到:
⎡⎣⎢⎢⎢⎢a0a1⋮an−1⎤⎦⎥⎥⎥⎥=1n⎡⎣⎢⎢⎢⎢⎢⎢(ω−0n)0(ω−1n)0⋮(ω−(n−1)n)0(ω−0n)1(ω−1n)1⋮(ω−(n−1)n)1⋯⋯⋱⋯(ω−0n)n−1(ω−1n)n−1⋮(ω−(n−1)n)n−1⎤⎦⎥⎥⎥⎥⎥⎥⎡⎣⎢⎢⎢⎢⎢A(ω0n)A(ω1n)⋮A(ωn−1n)⎤⎦⎥⎥⎥⎥⎥[a0a1⋮an−1]=1n[(ωn−0)0(ωn−0)1⋯(ωn−0)n−1(ωn−1)0(ωn−1)1⋯(ωn−1)n−1⋮⋮⋱⋮(ωn−(n−1))0(ωn−(n−1))1⋯(ωn−(n−1))n−1][A(ωn0)A(ωn1)⋮A(ωnn−1)]
于是只需要把 ωinωni 换成 ω−inωn−i (根据单位根性质4,只需要把 ωinωni 的虚部取其相反数即可),然后 DFTDFT ,然后将所得的结果除以 nn ,就可以实现 IDFTIDFT 了。
递归版FFT代码
有同学认为需要加一份递归版的代码。可惜是博主没有写过递归版的。于是就从网上拉了一份QAQ。
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
|
迭代版FFT与蝴蝶操作
你显然已经可以递归实现 FFTFFT 了。但是递归实现 FFTFFT 常数较大,代码又长,一般不写。
假设现在有 88 个数要进行 DFTDFT ,我们来看看递归的时候,每一个数的顺序以及二进制位的情况。
∣∣∣∣∣∣∣∣∣0000000000|0011244100||0102422010|0113666110|||1004111001|1015355101||1106533011|1117777111∣∣∣∣∣∣∣∣∣|000001010011100101110111012345670246|135704|26|15|370|4|2|6|1|5|3|7000100010110001101011111|
稍微观察一下,你就会发现,分治到边界之后的下标是原下标的二进制位翻转。
于是我们只需要预处理每一个数的二进制位翻转后的结果,并在 FFTFFT 开始前交换所有数与他翻转之后的数。具体可以参见后面的代码。
蝴蝶操作
在合并两个子问题的过程中,假设 A0(ωkn2)A0(ωn2k) 和 A1(ωkn2)A1(ωn2k) 分别保存在 akak 和 an2+kan2+k 中,而 A(ωkn)A(ωnk) 和 A(ωk+n2n)A(ωnk+n2) 将会被放在之后的 akak 和 an2+kan2+k 中,为了避免覆盖原值出错,我们加入一个临时变量,并实现以下三个操作:
tmp←ωkn×an2+ktmp←ωnk×an2+k
an2+k←ak−tmpan2+k←ak−tmp
ak←ak+tmpak←ak+tmp
这个操作被叫做蝴蝶操作。
迭代版FFT模版 -UOJ#34多项式乘法
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 |
|
数论变换(Number-Theoretic Transform,NTT)
FFTFFT 虽然能快速处理卷积,但是它也有很大的弊端。精度问题有时会导致一些错误。而且,有许多题目涉及了取模,比如 998244353998244353 ,复数域下的 DFTDFT 精度更是暴露无遗。于是考虑是否有模意义下的这种算法。于是,便出现了快速数论变换(Fast Number−Theoretic Transform, FNTFast Number−Theoretic Transform, FNT)。
虽然之前列举了一些单位根的性质,但是 FFTFFT 用到的却和我列举的有些差别。
于是我们回顾一下 FFTFFT 利用了单位根的什么性质。
1. ωnn=1ωnn=1
2. ω1n,ω2n,⋯,ωn−1nωn1,ωn2,⋯,ωnn−1 互不相同,满足了点值表示的条件。
3. ω2n=ωn2,ωn2+kn=−ωknωn2=ωn2,ωnn2+k=−ωnk ,这个是分治的基础。
4. ω−kn=conj(ωkn)ωn−k=conj(ωnk)
∑n−1k=0(ωj−in)k={0n(i≠j)(i=j)∑k=0n−1(ωnj−i)k={0(i≠j)n(i=j)
这个是IDFTIDFT的基础。
原根
我们需要找满足上面的性质的整数。
于是我们找到了原根。
对于一个质数 pp ,其 原根 gg 满足 g0,g1,g2,⋯,gp−2g0,g1,g2,⋯,gp−2 在模 pp 意义下两两不同。
可以发现, nn 需要是 p−1p−1 的因数,才能满足条件。由于 nn 是 22 的幂,所以对 pp 也有一定的要求。
pp 得是形如 r⋅2k+1r⋅2k+1 的素数,其中 2k≥n2k≥n 。
有一些非常常见的 NTTNTT 模数:
998244353=119×223+1998244353=119×223+1 ,原根为 33 。
1004535809=479×221+11004535809=479×221+1 ,原根为 33 。
更多 NTTNTT 模数 ⟹⟹ http://blog.miskcoo.com/2014/07/fft-prime-table
现在我们来证明一下原根满足上面的那些性质。
令 gnn≡1 (modp),(即gn≡gr (modp))gnn≡1 (modp),(即gn≡gr (modp)) ,等价于 ωnωn 。
1. ωnn=1ωnn=1
根据定义,显然成立。
2. ω1n,ω2n,⋯,ωn−1nωn1,ωn2,⋯,ωnn−1互不相同
根据原根的定义,也显然成立。
3. ω2n=ωn2,ωn2+kn=−ωknωn2=ωn2,ωnn2+k=−ωnk
由于 gn≡gr (modp)gn≡gr (modp) ,其中由于 nr=p−1nr=p−1 ,当 nn 取 n2n2 时, rr 取 2r2r,所以 gn2≡g2r≡(gr)2≡g2n (modp)gn2≡g2r≡(gr)2≡gn2 (modp) 。
由费马小定理可得 gp−1−1≡(gp−12+1)(gp−12−1)≡0(modp)gp−1−1≡(gp−12+1)(gp−12−1)≡0(modp) ,所以 gp−12≡±1(modp)gp−12≡±1(modp) 。又由于 gg 为原根,满足第 22 条性质。由于 g0≡1(modp)g0≡1(modp) ,所以 gp−12≡−1(modp)gp−12≡−1(modp) 。于是:
gn2n≡gp−12≡−1(modp)gnn2≡gp−12≡−1(modp)
即 gn2+kn≡gkn×gn2n≡−gkn(modp)gnn2+k≡gnk×gnn2≡−gnk(modp) 。
4. ∑n−1k=0(ωj−in)k={0n(i≠j)(i=j)∑k=0n−1(ωnj−i)k={0(i≠j)n(i=j)
由于 44 的第一项不是很重要,所以可以不管(直接逆元算算就好了)。
∑k=0n−1gk(j−i)n≡{n∑n−1k=0(gj−in)k≡1−(gj−in)n1−gj−in≡0(i=j)(i≠j)(modp)∑k=0n−1gnk(j−i)≡{n(i=j)∑k=0n−1(gnj−i)k≡1−(gnj−i)n1−gnj−i≡0(i≠j)(modp)
于是,综上所述,原根满足了 FFTFFT 要用到的单位根的性质,于是我们可以把单位复根替换成原根,再写个和 FFTFFT 差不多的就可以了。
NTT参考代码 - 51Nod1028 大数乘法 V2
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 |
|
注意,从本节以后,请注意观察式子中是否有卷积形式
"ai=∑ij=0bjci−jai=∑j=0ibjci−j"。
分治FFT
顾名思义,分治 FFTFFT 就是分治再加上 FFTFFT 嘛。
考虑有如下的递推式:
ai=∑j=1ikjai−jai=∑j=1ikjai−j
其中 kk 数组以及 a0a0 给出。
我们发现这个式子非常像多项式卷积的形式,但是显然不能所有的 aiai 一起计算,就是说一次 FFTFFT 显然不能解决问题。
于是我们可以分治 FFTFFT 。
定义 solve(L,R)solve(L,R) 为“在 LL 之前的 aiai 都已经得到答案的基础上完成 LL ~ RR 的计算”。
于是,我们可以写出下面的这个伪代码:
| 1 2 3 4 5 6 |
|
其中在写代码的时候边界情况可能会有所不同。
但是读者请注意,上面 FFT()FFT() 里处理的不是右区间受到的全部贡献,只是完成了左区间对于右区间的贡献,事实上,一个 aiai 会分成大约 O(logn)O(logn) 次来贡献。
拆系数FFTFFT和三模数NTTNTT
毛啸2016的集训队论文有写,本节内容许多摘自他的论文,读者可以直接查阅他的论文。
经典的 FFTFFT 的虽然很好用,但是在一些数据范围较大的题目之下,还是要挂。
当两个长度为 105105 级别的序列卷积,模数为 109109 级别(不为 NTTNTT 模数),直接 FFTFFT 的话,每个数的结果大约在 10231023 左右,超出了 264264 ,一方面会使浮点数出现较大的误差,一方面你也不可能把他转成 6464 位整形然后取模,这个时候就要用下面的两种方法了。
拆系数FFTFFT
我们设 MM 为模数的大小,则取 M0=⌈M−−√ ⌉M0=⌈M ⌉ ,根据带余除法将所有的 xx 表示成 x=k[x]M0+b[x]x=k[x]M0+b[x] 。其中 k[x]k[x] 和 b[x]b[x] 为整数。
我们假设多项式 A(x)A(x) 的系数序列为 aiai ,多项式 B(x)B(x) 的系数序列为 bibi ,那么我们把 k[ai],b[ai],k[bi],b[bi]k[ai],b[ai],k[bi],b[bi] 形成的四个序列两两卷积,卷积结果大约在 10141014 级别,可以接受。并先取个模,然后乘上相应的系数,一起加到答案里面就可以了。这样要 77 次 (I)DFT(I)DFT 。通过 myy 论文里面讲的优化方法可以优化到 44 次甚至 3.53.5 次DFTDFT。
三模数NTTNTT
我们找 33 个大小在 109109 级别的 NTTNTT 模数。然后分别在这三个模数意义下求卷积结果,然后中国剩余定理合并即可。
具体方法:我们假设模数分别是 mod0,mod1,mod2mod0,mod1,mod2 ,先合并前两个模数,也就是求出答案在模 mod0×mod1mod0×mod1 意义下的值,然后用逆元将模 mod0×mod1×mod2mod0×mod1×mod2 意义下的数,也就是答案表示成 k×mod0×mod1+bk×mod0×mod1+b 的形式,这个东西我们不必真正求出,我们只需要在模 MM 意义下求即可,这样只需要使用 6464 位整型即可。
但这个需要 99 次 DFTDFT 效率没有上面的那个快。
(而且博主太菜了没写过,目前只写过 99 次 DFTDFT 的拆系数 FFTFFT (截至2018-04-17))
套路与例题
以下例题的链接是详细题解,题解里面有题目链接
套路1 - 字符串匹配
当我们从母串的某一个位置开始和模式串匹配的时候:
首先,我们发现需要匹配的字符对的标差会是定值,所以我们一般会把其中一个字符串进行翻转,因为翻转之后,需要匹配的字符对的下标之和为定值,这样才能满足卷积形式。(下面是翻转字符串之后,匹配连线的示意图)

放例题:
(注意,在此之后,我默认你已经能对是否翻转有敏感的认识)
BZOJ4053 两个串
题意
给定两个字符串 S 和 T ,回答 T 在 S 中出现了几次,在哪些位置出现。注意 T 中可能有 ? 字符,可以匹配任何字符。串长 ≤105≤105
提示
考虑到有通配符 ?? ,我们不能直接 KMP 。
但是我们可以通过构造卷积,通过判断卷积结果的某一位是否为 0 来确定某一个位置开始是否可以匹配。
可以从相同字符值差为 0 以及通配符与其他字符永远匹配方面来考虑。
第一道题,可以看看题解。
BZOJ4259 残缺的字符串
题意
给你两个串,用其中一个来匹配另一个。问从母串的那些位置开始可以匹配模式串。注意有"*"可以匹配任何字符。
串长 ≤3×105≤3×105 。
提示
和上一题唯一的区别就是两个串中都有通配符。基本上一样的。只是要稍微卡下时间和空间。
CodeForces 528D Fuzzy Search
题意
给你两个串 A,B(|A|≥|B|)A,B(|A|≥|B|) ,以及一个 kk 。
其中 AiAi 与 BjBj 匹配的条件是 Ai−k…i+kAi−k…i+k 中至少有一个与 BjBj相同。
问 BB 能在 AA 中匹配多少次。
字符集: {′A′,′C′,′G′,′T′}{′A′,′C′,′G′,′T′} 。
|B|≤|A|≤2×105,k≤2×105|B|≤|A|≤2×105,k≤2×105
提示
可以预处理每一个位置可以匹配到 {′A′,′C′,′G′,′T′}{′A′,′C′,′G′,′T′} 的哪些。
然后,如果按照之前两题的套路来构造卷积,先不谈常数巨大,手工展开都很困难。
注意到字符集非常小,我们可以考虑对于每一个字符分开考虑,构造卷积。
套路2 - 卷积形式变形
BZOJ3527 [ZJOI2014]力
题意
给出长度为 mm 的序列 q1..mq1..m ,让你输出长度为 mm 的序列 E1..mE1..m 。
其中:
Ei=∑j=1i−1qj(i−j)2−∑j=i+1mqj(i−j)2Ei=∑j=1i−1qj(i−j)2−∑j=i+1mqj(i−j)2
提示
将原式写成两个卷积式。其中一个很容易 FFTFFT ,另外一个可以通过翻转和更改求和指标等一系列推导变成 FFTFFT 擅长的卷积形式。
套路3 - 背包问题相关
有时候,我们会碰到类似无限背包的问题。给定一些物品的体积,问用这些物品可以拼出某个范围内的哪些体积。
构造多项式:如果有体积为 ii 的物品,则 ii 次项系数为 11 ,否则为 00 。特别的,我们手工添加一个 00 体积的物品。然后多项式平方一下,有值的位置所代表的体积就是可以通过至多 22 个体积值相加得到。然后我们顺手把所有有值的改成 11 。再平方,得到的是至多 44 个体积值相加得到的体积。平方 kk 次,就能得到至多 2k2k个物品体积相加可以得到的所有体积。复杂度 O(nlog2n)O(nlog2n) 。其中 nn 为体积范围。
CodeForces 268E Ladies' Shop
题意
首先,给你 nn 个数(并告诉你 mm ),分别为 p1…np1…n 。
让你求一个数的集合,满足:
当且仅当从这个数的集合中取数(可以重复)求和时(设得到的和为 sumsum ),如果 sum≤msum≤m ,则数 sumsum 在给你的 nn个数之中。
如果没有这种集合,输出 NONO 。
否则,先输出 YESYES ,然后输出这个集合最小时的元素个数,并输出集合中的所有元素。
1≤n,m≤106,1≤pi≤1061≤n,m≤106,1≤pi≤106
提示
考虑思考本题的特殊性,在本题之前的小例子的基础上,舍去无用的运算。
套路4 - 分治FFTFFT
BZOJ4836 [Lydsy1704月赛]二元运算
题意
定义二元运算 optopt 满足
x opt y={x+yx−y(x<y)(x≥y)x opt y={x+y(x<y)x−y(x≥y)
现在给定一个长为 nn 的数列 aa 和一个长为 mm 的数列 bb ,接下来有 qq 次询问。每次询问给定一个数字 cc 你需要求出有多少对 (i,j)(i,j) 使得 ai opt bj=cai opt bj=c 。
提示
在分治 aiai 的值域的时候,左右区间内的数会满足左区间严格小于右区间,这是个很好的性质,会便于你按照上面的式子分类贡献, FFTFFT 优化。
CodeForces 553E Kyoya and Train
题意
一个有 nn 个节点 mm 条边的有向图,每条边连接了 aiai 和 bibi ,花费为 cici 。
每次经过某一条边就要花费该边的 cici 。
第 ii 条边耗时为 jj 的概率为 pi,jpi,j 。
现在你从 11 开始走到 nn ,如果你在 tt 单位时间内(包括 tt )到了 nn ,不需要任何额外花费,否则你要额外花费 xx 。
问你在最优策略下的期望花费最小为多少。
(注意你每走一步都会根据当前情况制定最好的下一步)
提示
本题是 myy 的论文题,思维含量较大。
首先我告诉你 O(mTlog2T)O(mTlog2T) 的复杂度可以过。
先考虑 DPDP ,然后通过设一个期望贡献累加器,来化简 DPDP转移方程,并从中挖掘 FFTFFT 擅长的卷积形式,并通过分治 FFTFFT优化。
杂题
BZOJ3160 万径人踪灭
题意
给你一个只含 a,ba,b 的字符串,让你选择一个子序列,使得:
1.1. 位置和字符都关于某一条对称轴对称。
2.2. 不能是连续的一段。
问原来的字符串中能找出多少个这样的子序列。答案对 109+7109+7 取模。
串长 ≤105≤105 。
提示
先避开条件2考虑如何解题。考虑一个点为中心,在其两侧能互相匹配的字符对数。每一对可以互相匹配的都可以选择选或者不选。从中寻找卷积形式。
对于不满足2的,显然是连续回文子串个数, ManacharManachar 裸题。
BZOJ4451 [Cerc2015]Frightful Formula
题意
给你一个 n×nn×n 矩阵的第一行和第一列,其余的数通过如下公式推出:
fi,j=a⋅fi,j−1+b⋅fi−1,j+cfi,j=a⋅fi,j−1+b⋅fi−1,j+c
求 fn,nmod(106+3)fn,nmod(106+3) 。
提示
考虑每一个格子各自对于 fn,nfn,n 的贡献。
对于除了第一行和第一列的格子,性质相似,可以列出求和式子。再通过推导,寻找利于 FFTFFT 的卷积形式。
BZOJ4827 [Hnoi2017]礼物
题意
有两个长为 nn 的序列 xx 和 yy ,序列 x,yx,y 的第 ii 项分别是 xi,yixi,yi 。
选择一个序列 AA ,现在你可以对它进行如下两种操作:
1.1. 得到一个和 AA 循环同构的序列 A′A′ 。
2.2. 给所有的 A′iAi′ 都加上 c(c∈N+)c(c∈N+) ,得到序列 A′′A″ 。
你进行上面两个操作之后,得到的序列分别为 x′′,y′′x″,y″ (注意 x,yx,y 两个序列中至少有一个序列没有发生任何变化)
序列 x′′x″ 和 y′′y″ 的差异值为
∑i=1n(x′′i−y′′i)2∑i=1n(xi″−yi″)2
问差异值最小为多少。
提示
考虑先写出一个一般的结果式子,然后略微展开,得到一些常数,一个关于 cc 的二次函数和一个卷积式。
对于二次函数我们求一下最值即可。
对于卷积式,我们考虑求其最值。先倍长某一个串,再翻转某一个串, FFTFFT 优化,计算出你需要的东西。
CodeForces 958F3 Lightsabers (hard)
题意
有 nn 个球,球有 mm 种颜色,分别编号为 1⋯m1⋯m ,现在让你从中拿 kk 个球,问拿到的球的颜色所构成的可重集合有多少种不同的可能。
注意同种颜色球是等价的,但是两个颜色为 xx 的球不等价于一个。
1≤n≤2×105, 1≤m,k≤n1≤n≤2×105, 1≤m,k≤n。
提示
一道比较新的题目,是我写这篇博文前几天的 CodeForcesCodeForces上的 ACMACM 比赛题。
考虑构造一些小的多项式,然后把他们全部乘起来得到最终的解。
需要分治或者启发式合并优化。建议启发式合并。
CodeForces 623E Transforming Sequence
题意
给定 n,kn,k 。
让你构造序列 a(0<ai<2k)a(0<ai<2k) ,满足 bi(bi=a1 or a2 or ⋯ or ai)bi(bi=a1 or a2 or ⋯ or ai) 严格单调递增。( oror 为按位或)
问你方案总数。对 109+7109+7 取模。
n≤1018,k≤30000n≤1018,k≤30000
提示
又是一道 myy 论文题。
思维含量也挺大的。
先考虑暴力 DPDP ,然后考虑加大转移的步长,从已经得到的 dpdp 值中状态转移得到新的 dpdp 值。需要寻找你得到的加大步长后的 dpdp 转移方程的利于 FFTFFT 的卷积形式,然后倍增 FFTFFT 优化。
参考文章与博客&鸣谢
(特别鸣谢)http://blog.miskcoo.com/2015/04/polynomial-multiplication-and-fast-fourier-transform#comment-37058
2016国家队候选队员论文 - 毛啸 - 再探快速傅里叶变换
http://picks.logdown.com/posts/177631-fast-fourier-transform
http://picks.logdown.com/posts/247168-fast-fourier-transform-modulo-prime