单元最短路和多源汇最短路的适用算法
摘要
本文主要介绍关于图的最短路的五种常用算法和其应用。朴素Dijkstra, 堆优化Dijkstra,Bellman-Ford,SPFA, Floyd。这几种算法有各自的优势和劣势,适用于不同的场景。
另:本篇文章篇幅较长,但难度不大, 建议学习算法的同时,自己手动画图,并模拟算法流程,将会一目了然,所见即所得!
单源最短路: 一个点到其他点的最短路。
无负边权时适用算法(所有边长都为正数):
-
稠密图: 朴素Dijkstra
-
稀疏图: 堆优化Dijkstra, SPFA
有负边权时适用算法:
- SPFA
- Bellman-Ford
求有边数限制的单源最短路:
- Bellman-Ford
多源汇最短路: 任意两点间的最短路。
- Floyd
图的存储方式
存储稠密图时,使用邻接矩阵。
存储稀疏图时,使用邻接表。
稠密图是指边数远大于点数,稀疏图是边数和点数差不多相等。
以n表示点数, m表示边数,
一般来说题目数据是n < 100, m < 10000 的图是稠密图, 是n<10000, m<10000的图是稀疏图。
朴素Dijkstra
算法思想:
朴素DijKstra的思想是通过一个距离起点A最近的点B,缩短起点A通过点B到达其他点的距离,因为只有通过距离起点最近的点,才有可能缩短起点到达其他点的距离。
所以一共分两步:
第一步:找到距离起点最近的点。
第二步:通过该点缩短起点到达其他点的距离。
比如:

对于AB和AC, AB为3, AC 为6,AB是A到其他点的最短距离,如果AC有可能更小的话,那么一定是经过B。原本A到C是6, 但经过B, ABC的距离是4.所以AC的最短距离是4.
所以怎么实现呢?
- 我们设置一个dis数组,来表示其他点到起点的最短距离。起点到起点的距离是0,所以dis[1] = 0, 其他点现在到起点的距离全部设为正无穷。
- 然后,我们要找到一个距离起点最近点。用一个循环遍历一下。
int min = INF; // 表示还没有处理过的距离起点最近的点。
// 找出距离起点最近的点。
for(int j = 1; j <= n; j++){
if(st[j]==0 && st[min] > st[j])
min = j;
}
所以min就是我们找到的还没有处理过的距离起点最近的点。
处理的意思就是已经确定该点的最短路径。
然后通过min这个点,去缩短起点到达其他点的距离。
for(int j = 1; j <= n; j++){
dis[j] = max(dis[j], dis[j] + w[min][j])
}
核心代码:
public static int Dijkstra(){
Arrays.fill(dis, 0x3f3f3f3f);
dis[1] = 0;
for(int i = 0; i < n; i++){ // 循环n次, 每次找出一个离起点最近的点。
int t = -1;
for(int j = 1; j <= n; j++){
if(S[j] == 0 && (t == -1 || dis[t] > dis[j])){ // 找到一个距离最短的加入S集合。
t = j;
}
}
S[t] = 1; // 然后通过这个点来缩短原点到达其他点的距离。
for(int j = 2; j <= n; j++){
dis[j] = Math.min(dis[j], dis[t] + w[t][j]);
}
}
if(dis[n] != 0x3f3f3f3f) return dis[n];
else return -1;
}
例题:Dijkstra求最短路

JAVA代码:
import java.io.*;
import java.util.*;
public class 朴素Dijkstra{
static BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
static BufferedWriter out = new BufferedWriter(new OutputStreamWriter(System.out));
static final int N = 505;
static int w[][] = new int[N][N];
static int dis[] = new int[N]; // 每个点距离原点的距离。
static int S[] = new int[N]; // 最短路集合
static int n,m;
public static int Int(String s){
return Integer.parseInt(s);
}
public static int Dijkstra(){
Arrays.fill(dis, 0x3f3f3f3f);
dis[1] = 0;
for(int i = 0; i < n; i++){ // 循环n次, 每次找出一个离起点最近的点。
int t = -1;
for(int j = 1; j <= n; j++){
if(S[j] == 0 && (t == -1 || dis[t] > dis[j])){ // 找到一个距离最短的加入S集合。
t = j;
}
}
S[t] = 1; // 然后通过这个点来缩短原点到达其他点的距离。
for(int j = 2; j <= n; j++){
dis[j] = Math.min(dis[j], dis[t] + w[t][j]);
}
}
if(dis[n] != 0x3f3f3f3f) return dis[n];
else return -1;
}
public static void main(String[] args) throws Exception{
String s[] = in.readLine().split(" ");
n = Integer.parseInt(s[0]);
m = Integer.parseInt(s[1]);
for(int i = 0; i < n; i++)
Arrays.fill(w[i], 0x3f3f3f3f);
for(int i = 0; i < m; i++){
String s1[] = in.readLine().split(" ");
int a, b, c;
a = Int(s1[0]);
b = Int(s1[1]);
c = Int(s1[2]);
w[a][b] = Math.min(w[a][b],c);
}
out.write(Dijkstra()+"\n");
out.flush();
}
}
堆优化Dijkstra
算法思想:
堆优化其实就是使用优先队列对图BFS一遍,在搜索的同时更新点的距离。
朴素算法需要遍历所有点找出距离最近的点,使用优先队列使这一步的时间复杂度从n变为了logn。
对于走迷宫问题,我们很容易可以使用BFS找出最短路,因为每个点与点之间的距离是一样的,但是当边权不同时,显然我们必须先遍历近距离的点,这时我们就可以使用优先队列来达到这一目的。
关键代码:
public static int Dijkstra(){
Arrays.fill(dis, INF); // 初始化dis数组为正无穷
q.add(new Pair(0, 1)); // 将起点当做一个距离起点最近的点加入优先队列。
dis[1] = 0; // 起点到起点的距离是1.
while(!q.isEmpty()){ // 广度优先搜索 + 堆优化。
Pair t = q.poll();
if(S[t.a] == 1) continue;
S[t.a] = 1;
for(int i = h[t.a]; i != 0; i = ne[i]){ //搜索当前点的所有邻接点。
if(dis[e[i]] > t.w + w[i]){ // 更新距离
dis[e[i]] = t.w + w[i];
q.add(new Pair(dis[e[i]], e[i]));
}
}
}
if(dis[n] != INF) return dis[n]; // 可以到达n号点
else return -1;
}
}
还是上个题目使用堆优化来做:
import java.io.*;
import java.util.*;
class Pair{
int w;
int x;
Pair(int a, int b){
w = a;
x = b;
}
}
public class 堆优化Dijkstra{
static BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
static BufferedWriter out = new BufferedWriter(new OutputStreamWriter(System.out));
static final int N = 100010, INF = 0x3f3f3f3f;
static int n, m;
static int[] w = new int[N], dis = new int[N];
static int[] e = new int[N], ne = new int[N], h = new int[N], S = new int[N];
static int idx = 1;
static PriorityQueue<Pair> q = new PriorityQueue<>(11, new Comparator<Pair>(){
public int compare(Pair a, Pair b) {
return a.w - b.w;
}
});//自定义类需要重写比较器
public static void add(int a, int b, int c){
e[idx] = b;
w[idx] = c;
ne[idx] = h[a];
h[a] = idx++;
}
public static int Int(String s) {return Integer.parseInt(s);}
public static int Dijkstra(){
Arrays.fill(dis, INF);
q.add(new Pair(0, 1));
dis[1] = 0;
while(!q.isEmpty()){ // 广度优先搜索 + 堆优化。
Pair t = q.poll();
if(S[t.x] == 1) continue;
S[t.x] = 1;
for(int i = h[t.x]; i != 0; i = ne[i]){ // h[i]中存的是第i条个点指向的点。
if(dis[e[i]] > t.w + w[i]){
dis[e[i]] = t.w + w[i];
q.add(new Pair(dis[e[i]], e[i]));
}
}
}
if(dis[n] != INF) return dis[n];
else return -1;
}
public static void main(String[] args) throws Exception{
String s[] = in.readLine().split(" ");
n = Int(s[0]);
m = Int(s[1]);
for(int i = 0; i < m; i++){
String s1[] = in.readLine().split(" ");
add(Int(s1[0]), Int(s1[1]), Int(s1[2]));
}
out.write(Dijkstra()+"\n");
out.flush();
}
}
Bellman-Ford
算法思想:
Dijkstra算法是以一个距离起点最近的点为基准点,缩减其邻接点到起点的距离,是贪心思想。
而Bellman-Ford算法是先将每个点到达起点的距离设为正无穷,然后直接暴力枚举所有边,如果一个点的距离可以被更新,就更新该点的距离。枚举一次至少可以得到一个点到达起点的距离,直接无脑枚举n次,就可以得到所有点到起点的最短距离。
核心代码:
void BellMan_Ford(){
Arrays.fill(dist, 0x3f3f3f3f); // 初始化dis数组为正无穷
dist[1] = 0;
for(int i = 0; i < n; i++){
for(int j = 0; j < m; j++){
if(dist[b] > dist[a] + t.w) //如果从a->b的距离加上dis[a] > dis[b] 则更新dis[b
dist[b] = dist[a] + t.w;
}
}
}
可以看到最核心的就是两个for循环。手动画画图还是很好理解的。
求总路径条数不多于K条的最短路径
如果我们对Bellman-Ford算法进行一些限制,它就可以用来求有边数限制的最短路问题。
比如要求1到n的不多于1条边的最短路径,如果1不能直接到n,那么最短路径的边数一定是大于1的,此时就无解。
画个图:

用Bellman-Ford算法对求上图中1号点到3号点的最短路:
for(int i = 0; i < n; i++){
for(int j = 0; j < m; j++){
if(dist[b] > dist[a] + w)
dist[b] = dist[a] + w;
}
}
第一次枚举所有边的过程中,先得到2号点到1号点的距离,然后得到3号点到一号点的距离。虽然外层循环只进行了一次,却得到了边数大于2的路径长度,这与我们想要得到边数不多于k条边的目的是冲突的,如果我们限制每次遍历所有边时最多只能修改某个点的直接后继,而不能修改一个点后继的后继,那么遍历所有边k次后,得到的结果就是边数不多于k条的最短路。
看图:
第一次遍历所有边:得到2,3的距离

第二次遍历所有边:得到4,6的距离

第三次遍历所有边:得到5的距离

怎么实现呢,很简单,对每个点的距离进行更新时,用上一次更新后的结果去更新就行了。需要加个辅助数组去存储上一次更新后点的位置。
void BellmanFord(){
Arrays.fill(dist, 0x3f3f3f3f);
dist[1] = 0;
int[] last = new int[N];
for(int i = 0; i < k; i++){
System.arraycopy(dist, 0, last, 0, m); //将dist赋值给last
for(int j = 0; j < m; j++){
Pair t = p[j];
if(dist[t.b] > last[t.a] + t.x)
dist[t.b] = last[t.a] + t.x;
}
}
}
例题:有边数限制的最短路
Bellman-Ford算法时间复杂度很高,有人对其进行了优化,SPFA就是用队列优化版Bellman-Ford算法。
SPFA
我们知道Bellman-Ford是每次遍历所有边,如果一个点被搜索到了,就更新距离。 但是每一次遍历时是有一些点是无论如何都不会被搜索到的。这跟边的读入顺序有关。
比如读入:
2 3 1
1 2 1
代表2到3的距离是1, 1到2的距离是1
我们先存储的是2到3的边,所以就会先遍历2->3, 此时2和3到1的距离都是正无穷,所以3的距离不会被更新。
如果读入顺序是
1 2 1
2 3 1
我们一次循环就可以得到3号点的值。
算法思想:
我们在一次循环中做了很多不必要的操作,如果我们可以只更新那些前驱结点被更新过的点,就可以大大提升效率。因为只有前驱结点到达起点的距离减小了,它的后继结点到达起点的距离才能减小。
所以我们用宽搜的思想,每次将被更新过的点入队,然后遍历队列中每个点的后继结点,重复更新操作和入队操作。
虽然SPFA和堆优化版的Dijkstra很相似,但是两种搜索策略却是不同的。细细品。
核心代码:
public static void SPFA(){
Arrays.fill(dis, 0x3f3f3f3f);
dis[1] = 0;
q.add(1);
while(!q.isEmpty()){
int t = q.poll();
s[t] = 0; //出对后标记为0,因为可能存在负权边,所以一个点可能会被更新多次,
//所以一个点只要被更新过就能入队,次数不限
for(int i = h[t]; i != 0; i = ne[i]){
int j = e[i];
if(dis[j] > dis[t] + w[i]){
dis[j] = dis[t] + w[i];
if(s[j] == 0){// 如果该点当前不在队中,就入队,避免重复操作。
q.add(j);
s[j] = 1; //标记已在队中
}
}
}
}
}
堆优化Dijkstra和SPFA的区别和优缺点
两者虽然很像,而且思想上也有一些相似,但终究是两种不同的算法,
Dijkstra是以一个距离起点最近的点为基础去修改其邻接点,堆优化后,要对一个点的所有边进行堆排序,然后每次从最近的点开始遍历。但是,如果存在负边权,就不能保证当前点到起点的距离是最短的。比如
1->2 = 1 , 1->3 = 2, 3->2 = -2,
那么1->2的最短距离其实是0,而不是1。这就是为什么DijkStra不能处理负权边。
SPFA则不对边排序, 而是一股脑的遍历一个被更新过的点的所有边。因为省去了堆排序这一步骤,大部分时候SPFA是要快于堆优化的Dijkstra的。
但是!! SPFA可能会被网格图等特殊构造的图卡成o(nm)的时间复杂度,所以一般还是要用堆优化Dijkstra。但是!!如果有负边权,那么就只能用SPFA了。
用SPFA判断负环
负环:
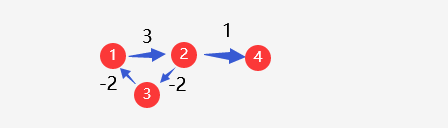
对于上图来说,1->2-> 3->1 就是一个负环,根据SPFA算法的性质,会将距离被更新过的点入队,因为存在负环,所以只要每次经过一次负环,所有点到起点的距离就会被不断减小,即SPFA就会陷入死循环,其他点到起点的距离最终会变为负无穷。
如果我们能找到一个条件,确定循环多少次后,就可以判断存在负环, 我们就可以强制结束SPFA,从而判断是否存在图中负环。
这个条件就是:
只要不存在负环,起点到达任意点所经过的边数一定小于n,反之一定大于等于n因为只有n个点,不经过环的话最多经过n-1条边,只有在存在负环的情况下,SPFA才会经过负环,经过负环后,到达其他点边数就会大于等于n,
代码:
public static int SPFA(){
//因为目的是判断有无负环,所以先要将所有点都当做起点加入队列,因为一个图可能分成不连通的几部分,而负环存在于其中某一个连通块。
for(int i = 1; i <= n; i++){
q.add(i);
}
while(!q.isEmpty()){// 这里不需要对dis数组初始化,因为存在负环的话距离会小于0.
int t = q.poll();
s[t] = 0;
for(int i = h[t]; i != 0; i = ne[i]){
int j = e[i];
if(dis[j] > dis[t] + w[i]){
dis[j] = dis[t] + w[i];
cnt[j] = cnt[t] + 1; // 将当前点到起点的距离+1
if(cnt[j] >= n){
return 1;
}
if(s[j] == 0){
q.add(j);
s[j] = 1;
}
}
}
}
return 0;
}
Floyd
先说说Floyd的优点
Floyd算法用来求任意两点间的最短路,我们当然可以用上面说过的算法如SPFA,对一个图的每个点都当成起点,求其最短路,但如果是稠密图,其时间复杂度也会很高,而Floyd算法实现十分简单,还能再O(n^3)内完成
Floyd是本次所有算法中最短的了!
对于算法来说,代码长的不一定难懂,但短的一定不会很难懂。
算法思想:
对于朴素Dijkstra算法来说,起点通过距离它最近的点去缩短其到达其他点的距离,Floyd算法本质上也是这样的思想。
第一步 :通过一个点,遍历所有点对,更新距离。
第二步:通过n个点,遍历所有点对n次,更新距离。
核心代码:
void floyd()
{
for (int k = 1; k <= n; k ++ ) //通过n个点
for (int i = 1; i <= n; i ++ ) // 遍历所有点对。
for (int j = 1; j <= n; j ++ )
arr[i][j] = min(arr[i][j], arr[i][k] + arr[k][j]);
}
第一层循环就是枚举n个点, 内部两层循环来枚举所有点对。
总结
- 一定要画图。
- 一定要刷题。
- 写题的时候一定要注意是不是无向图, 无向图的话建边时要建一来一去两条,如果用邻接表存,数组一定要开足够大,至少是边数的两倍。
- 对于邻接矩阵,要判断重边。邻接表则不需要判断重边。
最短路题单:
https://vjudge.net/contest/66569
POJ 2387 Til the Cows Come Home
POJ 2253 Frogger
POJ 1797 Heavy Transportation
POJ 3268 Silver Cow Party
POJ 1860 Currency Exchange
POJ 3259 Wormholes
POJ 1502 MPI Maelstrom
POJ 3660 Cow Contest
POJ 2240 Arbitrage
POJ 1511 Invitation Cards
POJ 3159 Candies
POJ 2502 Subway
POJ 1062 昂贵的聘礼
POJ 1847 Tram
LightOJ 1074 Extended Traffic
HDU 4725 The Shortest Path in Nya Graph
HDU 3416 Marriage Match IV
HDU 4370 0 or 1
POJ 3169 Layout
以上题单源自Kuangbin专题
基础算法合集:
https://blog.csdn.net/GD_ONE/article/details/104061907
