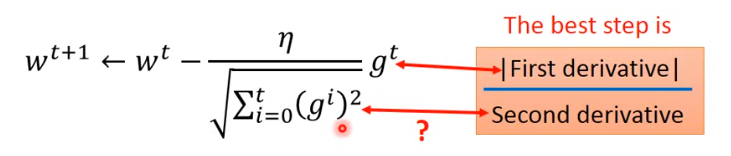机器学习入门之梯度下降

梯度下降回顾

在前篇文章中介绍的机器学习三步走第三步中，我们需要解决下面优化问题：

$\theta^*=arg\,\min_{\theta}L(\theta)$

假设 $\theta$向量有两个属性 $\{\theta_1,\theta_2\}$

初始从 $\theta^0$开始，

$\theta^0 =\left[ \begin{matrix} \theta^0_1 \\ \theta^0_2 \end{matrix} \right]$

接下来计算

$\left[ \begin{matrix} \theta^1_1 \\ \theta^1_2 \end{matrix} \right] = \left[ \begin{matrix} \theta^0_1 \\ \theta^0_2 \end{matrix} \right] -\eta \left[ \begin{matrix} \partial L(\theta_1^0) / \partial \theta_1 \\ \partial L(\theta_2^0) / \partial \theta_2\end{matrix} \right]$

这个步骤可以反复进行，再计算一次的话：

$\left[ \begin{matrix} \theta^2_1 \\ \theta^2_2 \end{matrix} \right] = \left[ \begin{matrix} \theta^1_1 \\ \theta^1_2 \end{matrix} \right] -\eta \left[ \begin{matrix} \partial L(\theta_1^1) / \partial \theta_1 \\ \partial L(\theta_2^1) / \partial \theta_2\end{matrix} \right]$
其中 $\eta$是初始学习率(learning rate)

上面的式子可以写得更加简洁：

$\nabla L(\theta) = \left[ \begin{matrix} \partial L(\theta_1) / \partial \theta_1 \\ \partial L(\theta_2) / \partial \theta_2\end{matrix} \right]$
$\nabla L(\theta)$叫做梯度。

也就是说:

$\left[ \begin{matrix} \theta^1_1 \\ \theta^1_2 \end{matrix} \right] = \left[ \begin{matrix} \theta^0_1 \\ \theta^0_2 \end{matrix} \right] -\eta \left[ \begin{matrix} \partial L(\theta_1^0) / \partial \theta_1 \\ \partial L(\theta_2^0) / \partial \theta_2\end{matrix} \right] \Longrightarrow \theta^1 = \theta^0 - \eta \nabla L(\theta^0)$

红色箭头是梯度向量，蓝色箭头是移动的方向。

小心的调整学习率

每种颜色都是不同的学习率。

如果学习率刚刚好，就像红色箭头所示；如果过小则向蓝色箭头，显得步长太小了；
若太大则像绿色箭头，那么永远到不了低点；甚至还可以过大，导致像黄色箭头那样。

如果是参数是一维或二维我们还可以画出这种图，如果参数超过3就没办法了。

我们还可以通过参数的变化来观察损失的变化。

可以通过观察损失函数的下降速度

x轴是学习率，y轴是Loss函数的值

因此学习率的调整很重要，简单的原则是：

• 开始时由于远离目标，因此使用大一点的学习率
• 在几次更新后，靠近目标了，因此减小学习率
• 每个参数给不同的学习率

比如可以选择 $\eta^t = \eta / \sqrt{t +1}$,其中 $t$是计算的次数，但是这样还不够。

接下来介绍一种比较好的梯度下降算法：Adagrad。

Adagrad

每个参数的学习率都除上之前算出来的微分值的均方根。

一般的梯度下降(批梯度下降,Vanilla Gradient descent)是这样的：

$w^{t+1} \leftarrow w^t - \eta^t g^t$ 其中 $w$是某一个参数，因为在做adagrad时，每个参数都有不同的学习率。
所以我们分别考虑每个参数。

$\eta^t = \frac{\eta} {\sqrt{t +1}}，g^t = \frac{\partial L(\theta ^t)}{\partial w}$
而Adagrad的做法是：

$w^{t+1} \leftarrow w^t - \frac{\eta^t}{\sigma^t}g^t$

$\sigma^t$是过去所有微分值的均方根。这个值对每个参数而言都是不一样的，因此是参数独立的。

我们来举个例子，假设初值为 $w^0$。

整个Adagrad的式子式是可以简化的:

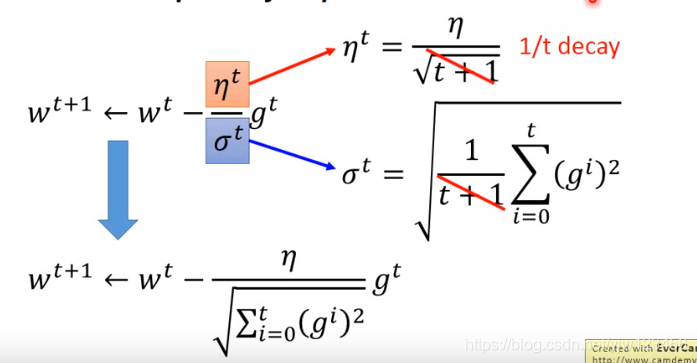
再回头来看下批梯度下降算法：

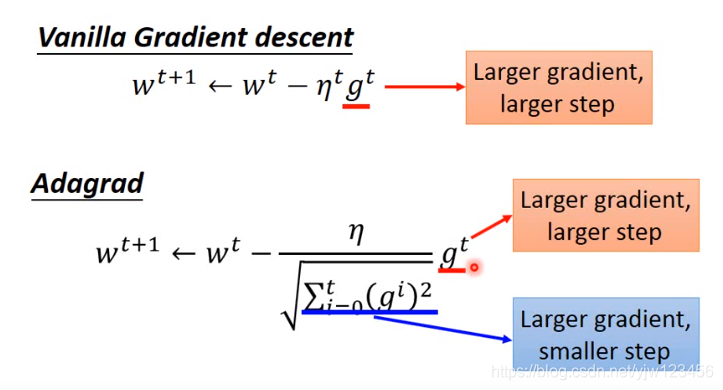
批梯度下降算法是梯度越大，步伐就越大；
而Adagrad是分子上，梯度越大，步伐越大；分母上，梯度越大，步伐越小。这里是否感觉有些矛盾。

我们来考虑一个二次函数： $y = ax^2 + bx + c$，它的图像如下：

把上式对 $x$做微分并取绝对值，得

$|\frac{\partial y}{\partial x}| = |2ax + b|$
它的图形为：

在二次函数上，假设初始点为 $x_0$，最低点是 $-\frac{b}{2a}$此时如果想找到最好的步伐多少

其实 $x_0$和 $-\frac{b}{2a}$之间的距离 $|x_0 + \frac{b}{2a}|$,整理一下可得 $\frac{|2ax_0 + b|}{2a}$

而 $|2ax_0 + b|$就是 $x_0$点的一次微分。

如果某点的微分值越大，则距离最低点越远；如果踏出去的步伐和微分大小成正比，则有可能是最好的步伐。

上面我们只考虑了一个参数，如果考虑多个参数上面的结论则不一定成立。

假设有两个参数，如果只考虑参数1，它的图像为：

其中a点的微分值大于b点，a点距离最低点更远。如果也考虑参数 $w_2$，它的图像是绿色的那个：

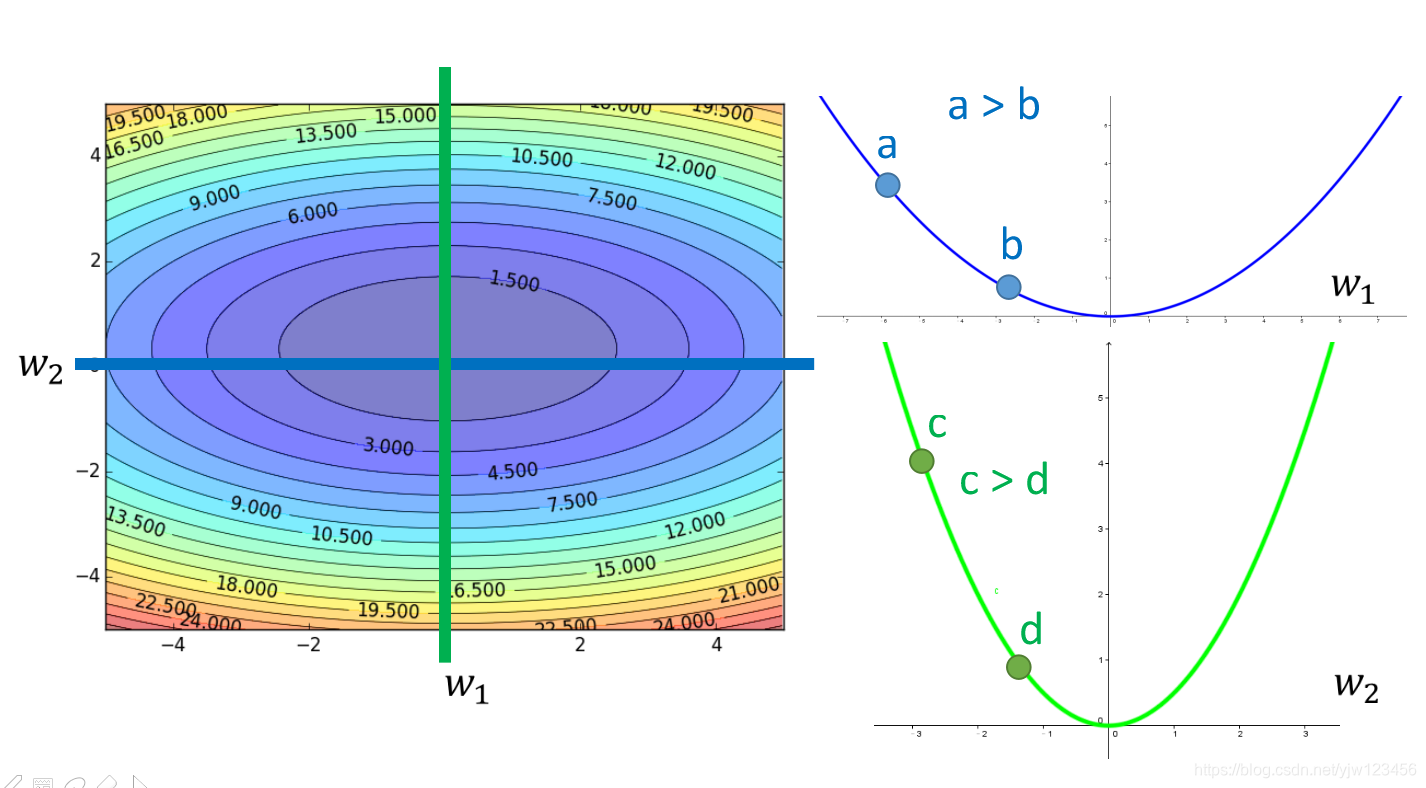
那，如果同时考虑这两个参数，如果同时考虑a点对 $w_1$的微分，c点对 $w_2$的微分。
c点处的微分值比较大，a点处的微分值小于它，但是c离低点比a离低点更近。

我们再回头看下最好的微分 $\frac{|2ax_0 + b|}{2a}$，发现它的分母上有个 $2a$。

我们把函数做二次微分得: $\frac{\partial^2y}{\partial x^2} = 2a$

也就是说，最好的步伐，它不仅和一次微分成正比，还和二次微分成反比。

那它和Adagrad的关系是什么？

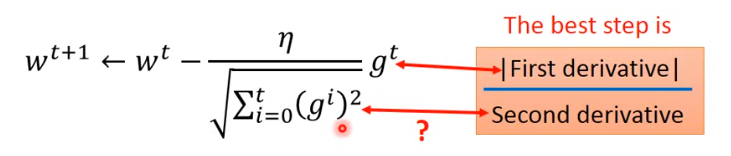
我们再来看下adagrad: $g^t$就是一次微分，那么它的分母是怎么和二次微分关联的呢？(derivative，导数)

adagrad用一次微分来估计二次微分：

我们考虑二次微分较小的图形（图左）和二次微分较大的图形（图右）。

然后把它们一次微分 $\sqrt{(一次微分)^2}$的图形考虑进来：

我们在一次微分图形上取很多个点，可以发现在二次微分较小的图形中，它的一次微分通常也较小。
而Adagrad中的 $\sqrt{\sum_{i=0}^t(g^i)^2}$就反映了二次微分的大小。

通过Adagrad实现梯度下降的代码：

def gradient_descent():
    x_data = [338, 333, 328, 207, 226, 25, 179, 60, 208, 606]
    y_data = [640, 633, 619, 393, 428, 27, 193, 66, 226, 1591]
    b = -120
    w = -4
    lr = 1 # 学习率
    lr_b = 0 # b的学习率
    lr_w = 0 # w的学习率
    iteration = 10000 #迭代次数
    for i in range(iteration):
        b_grad = 0.0
        w_grad = 0.0
        for n in range(len(x_data)):
            w_grad = w_grad - 2.0 * (y_data[n] - (b + w * x_data[n])) * x_data[n]
            b_grad = b_grad - 2.0 * (y_data[n] - (b + w * x_data[n])) * 1.0

        lr_b = lr_b +  b_grad ** 2
        lr_w = lr_w + w_grad ** 2

        b = b - lr/np.sqrt(lr_b) * b_grad
        w = w - lr/np.sqrt(lr_w) * w_grad

    print(b,w)

随机梯度下降法

随机梯度下降法( Stochastic Gradient Descent)可以训练的更快。

上篇文章中说到回归的损失函数为：

$L = \sum_{n}(\hat{y}^n -(b + \sum w_ix_i^n))^2 \\ \theta^i = \theta^{i-1} - \eta\nabla L(\theta^{i-1})$
损失考虑了所有的训练数据。

而随机梯度下降法，每次只取某一个训练数据 $x^n$出来：

而损失值只考虑现在的参数对该训练数据的的估测值减去实际值：

$L^n = (\hat{y}^n -(b + \sum w_ix_i^n))^2 \\ \theta^i = \theta^{i-1} - \eta\nabla L^n(\theta^{i-1})$

并且计算梯度的时候也只计算只针对该训练数据 $x^n$计算。

左边看完20个训练数据才更新损失值，右边每看一个训练数据，就更新一次损失值。

特征缩放

假设要根据以下函数做回归
$y = b + w_1x_1 + w_2x_2$

假设 $x_2$的分布比 $x_1$要大，就需要把 $x_2$的分布缩小，让它们一致。

举例来说

如果 $x_1$的分布是1,2,… 而 $x_2$的分布是 100,200,…
那么画出的损失值的图形是图左的样子；

如果进行缩放后，图形是正圆，很容易向着圆心走。可以极大提高算法的效率。

特征缩放的方法

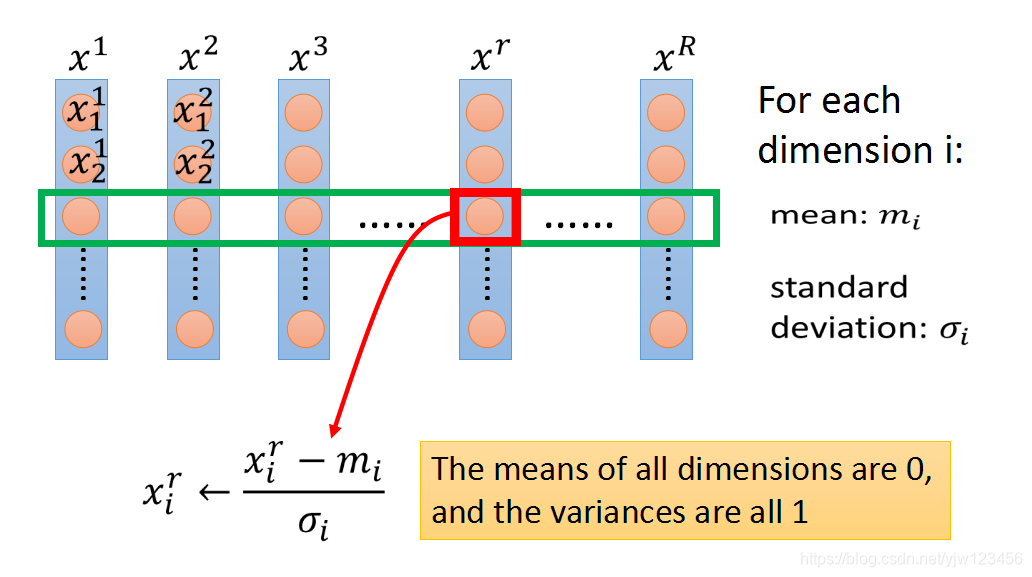
对每个维度，计算该维度的均值 $m_i = \frac{\sum x^r_i}{R}$和标准差 $\sigma_i = \sqrt{\frac{\sum(x_i^r-m_i)^2}{R}}$