梯度下降法/批量梯度下降法BGD
梯度下降法是一种基于搜索的最优化方法,即通过不断地搜索找到函数的最小值.并不是机器学习专属的方法.但是在机器学习算法中求解损失函数的最小值时很常用.
还记得之前说过的机器学习算法的普遍套路吗?
- 定义一个合理的损失函数
- 优化这个损失函数,求解最小值.
对有的损失函数来说,最小值是有着数学上的方程解的.但有的函数是不存在着数学解的,这时候我们就可以通过梯度下降法逐步地搜索,直到越来越逼近最优解.
首先我们要理解梯度的概念:
梯度的本意是一个向量(矢量),表示某一函数在该点处的方向导数沿着该方向取得最大值,即函数在该点处沿着该方向(此梯度的方向)变化最快,变化率最大(为该梯度的模)。
这里有篇很棒的讲解,帮助你理解梯度,主要是图很多,很直观.建议看看.
1. 基本概念 .这几个基本概念一定要搞清楚.
- 方向导数:是一个数;反映的是f(x,y,z...)沿方向v的变化率。
- 偏导数:是多个数(每元有一个).是指多元函数沿坐标轴方向的方向导数,因此二元函数就有两个偏导数。
- 偏导函数:是一个函数;是一个关于点的偏导数的函数。
- 梯度:是一个向量;每个元素为函数对一元变量的偏导数;它既有大小(其大小为最大方向导数),也有方向。
函数沿着梯度的方向增大最快。注意不要用一元函数的思维去思考这个结论.梯度是有方向的!不要把梯度和导数搞混了,比如$y=x^2$的导数y=2x,如果非要把导数表述成说梯度的话,梯度的方向其实是x轴.在x<0时,x处的导数为负,那么梯度为x轴反方向的向量,x>0时,梯度为x轴方向的向量,此时,函数沿着梯度的方向增大最快这个结论依然是成立的.
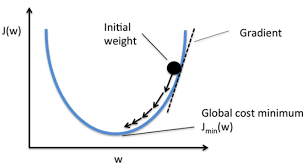
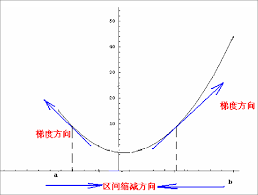
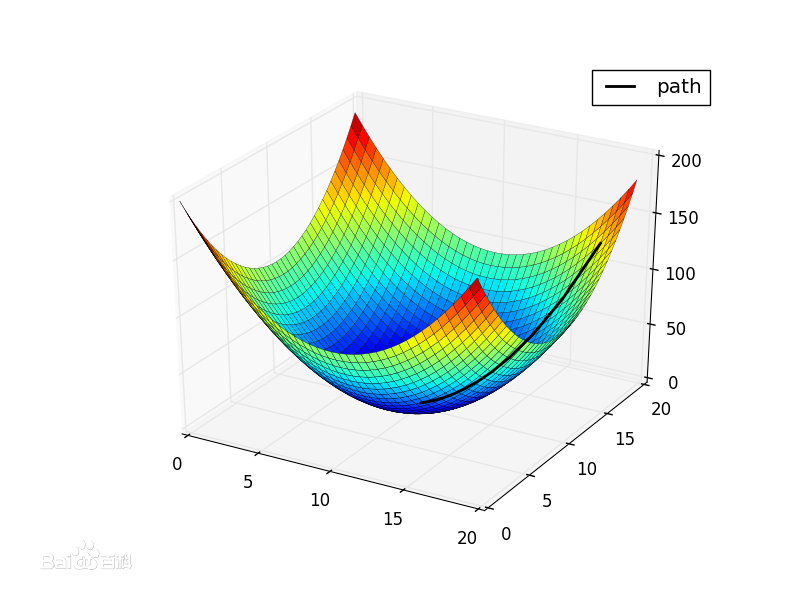
我们现在要求$J(\theta)$的最小值.则从某个点A开始,每次沿着A点的梯度的反方向移动$\eta$到点B,到达B点后,再沿着B点的梯度的反方向移动$\eta$,....,不断重复这个过程,最终就可以达到某一个极值点.
直观点说,比如我们在一座大山上的某处位置A,我们想下山,想最快地下山,于是我们求出A点梯度$\nabla_A$(这是一个向量,沿着这个方向的反方向即下山的最陡峭的路),然后移动$- \eta\nabla_A$到达位置B,求出$\nabla_B$,移动$- \eta\nabla_B$到达位置C,......不断重复这一过程,最终就达到了山底.也有可能只是局部的山底.
$\eta$称作学习率
- $\eta$影响获得最优解的速度
- $\eta$选取的不好 甚至无法找到最优解
对第一点很好理解,$\eta$太小了,势必要很久才能达到极值点.
对第二点,试想,如果$\eta$太大,则有可能错过极值点.比
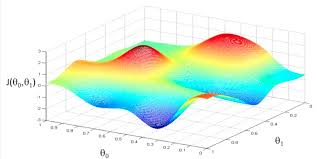
不是所有函数都只有唯一极值点的.所以梯度下降法找到的可能是局部最小值而不是全局最小值.结合下图理解一下.所以我们的起始搜索点就很重要了.
结合上面说的下山的例子理解一下,即
- 起始位置A很重要 实际使用中通常要多次随机生成这个A的位置,以避免找到的是局部最优解而不是全局最优解
- 学习率$\eta$很重要.需要我们不断调试.属于一个超参数.
- 通常在使用梯度下降法之前,需要对数据做归一化处理,避免某一维度数据尺度过大,影响梯度的值.影响收敛速度.
实现线性回归中的梯度下降法
机器学习笔记线性回归中我们推导出$f_{loss} = \sum_{i=1}^m(y^i - X_b^i \theta)^2$.之后如何求得$\theta$,可以使得对所有样本而言,损失最小.我们一笔带过了.这个函数是有着其数学解的.但是今天我们用梯度下降法求出$\theta$。
$$\nabla L(\theta) = \begin{bmatrix} \frac {\partial L} {\partial \theta_0} \\ \frac {\partial L} {\partial \theta_1} \\ \frac {\partial L} {\partial \theta_2} \\ … \\ \frac {\partial L}{\partial \theta_n} \\ \end{bmatrix} = \begin{bmatrix} \sum_{i=1}^m 2(y^{(i)}-X_b^{(i)}\theta)(-1) \\ \sum_{i=1}^m 2(y^{(i)}-X_b^{(i)}\theta)(-X_1^{(i)}) \\ \sum_{i=1}^m 2(y^{(i)}-X_b^{(i)}\theta)(-X_2^{(i)}) \\ … \\ \sum_{i=1}^m 2(y^{(i)}-X_b^{(i)}\theta)(-X_n^{(i)}) \\ \end{bmatrix}$$
伪码如下:
注意:未知数是theta,而不是X_b,y。
#某一种theta取值下 获取其对应的梯度向量
def get_gradient(X_b,y,theta):
return gradient #这里返回的是一个向量
#损失函数的大小
#def loss(X_b,y,theta):
return loss_value #当theta取某种值时,loss的大小 是一个数
def gradient_descent(init,eta,n,diff=1e-8): #init代表起始点位置 eta代表步长 n代表最大迭代次数
theta = init
i = 0
while i < n:
gradient = get_gradient(X_b,y,theta):
new_theta = theta - eta*get_gradient() #移动到新位置
#当两点直接损失函数值相差极小,说明我们已经逼近局部最小值
if abs(loss(X_b,y,theta) - loss(X_b,y,new_theta)) < diff: #类似与c++中判断浮点数是否为0.
break
theta = new_theta
这是代数方法,还有一种矩阵的方法求解$\theta$。矩阵转换转的头大,公式编辑又麻烦,就不写了. 不影响我们理解梯度下降法的原理.
随机梯度下降法SGD
$$\nabla L(\theta) = \begin{bmatrix} \frac {\partial L} {\partial \theta_0} \\ \frac {\partial L} {\partial \theta_1} \\ \frac {\partial L} {\partial \theta_2} \\ … \\ \frac {\partial L}{\partial \theta_n} \\ \end{bmatrix} = \begin{bmatrix} \sum_{i=1}^m 2(y^{(i)}-X_b^{(i)}\theta)(-1) \\ \sum_{i=1}^m 2(y^{(i)}-X_b^{(i)}\theta)(-X_1^{(i)}) \\ \sum_{i=1}^m 2(y^{(i)}-X_b^{(i)}\theta)(-X_2^{(i)}) \\ … \\ \sum_{i=1}^m 2(y^{(i)}-X_b^{(i)}\theta)(-X_n^{(i)}) \\ \end{bmatrix}$$
再来看一下这个梯度,可以看到,这个梯度的计算是与所有的样本有关的.当X_b很大,即样本数很多,特征很多时,这个计算量是巨大的.
这就引申出随机梯度下降法.在计算梯度时,只参考某一个样本,而不参考全部样本.
$$\nabla L(\theta) = \begin{bmatrix} \frac {\partial L} {\partial \theta_0} \\ \frac {\partial L} {\partial \theta_1} \\ \frac {\partial L} {\partial \theta_2} \\ … \\ \frac {\partial L}{\partial \theta_n} \\ \end{bmatrix} = \begin{bmatrix} 2(y^{(i)}-X_b^{(i)}\theta)(-1) \\ 2(y^{(i)}-X_b^{(i)}\theta)(-X_1^{(i)}) \\ 2(y^{(i)}-X_b^{(i)}\theta)(-X_2^{(i)}) \\ … \\ 2(y^{(i)}-X_b^{(i)}\theta)(-X_n^{(i)}) \\ \end{bmatrix}$$
这样的话,将极大地提高我们每一次搜索的速度,当然,代价就是牺牲了每一次搜索的准确度.因为每次只参考一个样本,导致每次搜索的方向是随机的.所以可能出现已经向最低点靠近了,可能下一次搜索又折回来了,以爬山举例,就是快到山底了,又朝上走了. 解决这个问题的方法通常是调整学习率,在梯度下降(也就是批量梯度下降)中,我们的学习率是固定的. 在随机梯度下降中,这个值随着搜索次数的增加,逐渐减少. 比如取迭代次数的倒数.
小批量梯度下降法MBGD
小批量梯度下降法,兼顾了批量梯度下降和随机梯度下降的优缺点,算是取了一个折中的方案. 每次计算梯度时,既不只参考一个样本,也不参考全部的样本,而是参考部分样本. 这种最常用.
sklearn中的使用
sklearn.linear_model.SGDRegressor
class
sklearn.linear_model.SGDRegressor(loss=’squared_loss’, penalty=’l2’, alpha=0.0001, l1_ratio=0.15, fit_intercept=True, max_iter=None, tol=None, shuffle=True, verbose=0, epsilon=0.1, random_state=None, learning_rate=’invscaling’, eta0=0.01, power_t=0.25, early_stopping=False, validation_fraction=0.1, n_iter_no_change=5, warm_start=False, average=False, n_iter=None)[source]¶
sklearn.linear_model.SGDClassifier
class
sklearn.linear_model.SGDClassifier(loss=’hinge’, penalty=’l2’, alpha=0.0001, l1_ratio=0.15, fit_intercept=True, max_iter=None, tol=None, shuffle=True, verbose=0, epsilon=0.1, n_jobs=None, random_state=None, learning_rate=’optimal’, eta0=0.0, power_t=0.5, early_stopping=False, validation_fraction=0.1, n_iter_no_change=5, class_weight=None, warm_start=False, average=False, n_iter=None)[source]¶
使用示例:
from sklearn.preprocessing import StandardScaler standardScaler = StandardScaler() standardScaler.fit(X_train) X_train_standard = standardScaler.transform(X_train) X_test_standard = standardScaler.transform(X_test) from sklearn.linear_model import SGDRegressor sgd_reg = SGDRegressor() sgd_reg.fit(X_train_standard, y_train) sgd_reg.score(X_test_standard, y_test)
最后感慨一下,写博客真的很累啊,自己懂了是一回事,把懂的用语言表达给别人,让别人也能懂,难度上升了一个级别.用文字表述出来,又要图文并茂浅显易懂,难度又上升了一个级别.希望自己可以坚持下去.
