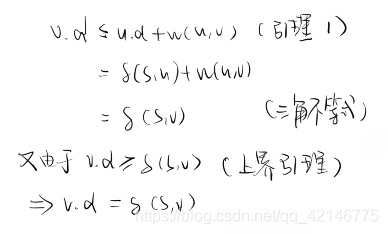学习自《算法导论》和Wiki

无权/权=1:BFS ——O(V+E)
有向图(非负边):Dijkstra——O(E+VlgV)
有向图(无环):Dijkstra——O(V+E)
一般(可正可负可环):Bellman-Ford———O(VE)
优化:SPFA
一丶BFS
BFS(G,s)
{
//初始化
foreach(v∈G.V){ v.visit=0;u.d=NIF; u.path=nil}
s.d=0;s.path=nil;s.visit=1;
//根节点进队
enqueue(Q,s)
while(Q not empty){
u=dequeue(Q)
foreach(v∈Adj[u])
if(visit[v]==0)
{
d.v=d.u+1;
v.path=u;
v.visit=1;
enqueue(Q,v);
}
}
- 复杂度分析
-
1.初始化成本O(V)
2.队列操作总时间为O(V)
3.每个结点进队和出队一次,只有出队时候才进行扫描,每个邻接链表最多扫描一次,所以用于扫描邻接表的总时间为O(E)
所以O(V+E)
松弛操作
每个结点v来说,我们维持一个属性v.d,用来记录从源节点s到节点v的最短距离估计,v.path记录v的前驱节点
我们使用init_single_source(G,s)对最短路径估计进行和前驱节点进行初始化
init_single_source(G,s)
{
foreach(v∈G.V)
{
d[v]= INF
v.path=NIL
}
s.d=0
}
Relax(u,v,w)
{
if(v.d>u.d+w(u,v))
{
v.d=u.d+w(u,v)
v.path=u
}
}
松弛操作首先尝试是否可以改善s,v的最短路径,可以就改善,所以松弛操作可以降低最短路径估计,更新前驱节点
后面的Dijkstra、Bellman-Ford、DAG都会使用init_single_source(G,s),然后重复的对边进行Relax(u,v,w)。不同之处在于Dijkstra和DAG对每条边仅松弛一次,而Bellman-Ford对每条边松弛|V|-1次

后面有证明
二丶Dijkstra
使用了广度优先搜索解决赋权有向图的单源最短路径问题
下图来自wiki

单源最短路径可以使用贪心证明
也就是证明局部最优达到全局最优证明
updating~~~

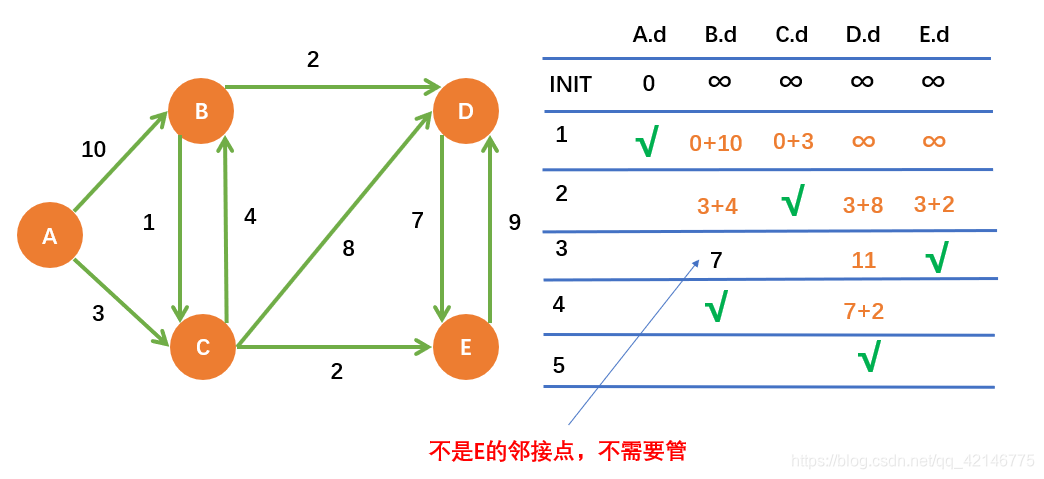
- 图解释
-
Dijkstra算法有两个点集合,一个就是已经知道了路径的S,还有就是未知的G-S,
图中 绿色点表示现在S可以直连的,也知道这些连接点边的长度
图中 红色点表示现在S不可以直连的,也不知道这些连接点边的长度,必须等其他点加入S后才能获取
图中 黑色点表示根本连接不上的点,不在一个连通分量中
Dijkstra 算法使用的就是单源最短路径贪心性质,每次选择S连接到的绿色点的路径集合中权值和最小的,然后把那个点u加入S
然后更新u的不属于S集合的邻居
Pseudocode
Dijkstra(G,W,s)
{
init_single_source(G,s)
Q=G.V
while(Q not empty)
{
u=Extract_Min(Q)
foreach(v∈Adj[u])
if(v∈Q)
Relax(u,v,w)
}
}
//这里Relax有一些其余操作使用优先队列需要Decrease_key(v)
Relax(u,v,w)
{
if(v.d>u.d+w(u,v))
{
v.d=u.d+w(u,v)
Decrease_key(v)
v.path=u
}
}
正确性证明

三丶DAG
DFS(G,s)
{
foreach(v∈G.V){ v.visit=0;u.d=NIF; u.path=nil}
s.visit=0;s.d=NIF; s.path=nil
foreach(u∈Adj[s])
if (u.visit!=1)
{
u.visit=1
DFS(G, u)
}
}
DAG_SP(G,w,s)
{
topologicalSort(G) //拓扑排序另一篇有讲
init_single_source(G,s)
foreach(v∈G.V)
foreach(v∈Adj[u])
Relax(u,v,w)
}
四丶Bellman_Ford
关键是这个算法可以用于分布式系统,因为操作纯粹是局部的,松弛也是局部的,你不需要任何整体策略,上面我们对于每条边的更新是固定顺序,我们完全可以选择随机顺序,我们只要不断松弛边,最终这个算法可以保证在|V|-1次找到最短路径,虽然分布式系统可能不是同步的,而且分析也复杂一些,但还是行得通,最终会收敛。经常用于求网络上的最短路径比如结点就是网络机器,连线就是线路,在计算机网络中距离矢量路由就是用的这种道理

Pseudocode
Bellman_Ford(G,W,s)
{
init_single_source(G,s)
for(i:1->|V|-1)
foreach((u,v)∈G.E)
Relax(u,v,w)
foreach((u,v)∈G.E) //n次操作仍可降低花销,就一定存在负权环
if(v.d>u.d+w(u,v))
say("error")
}

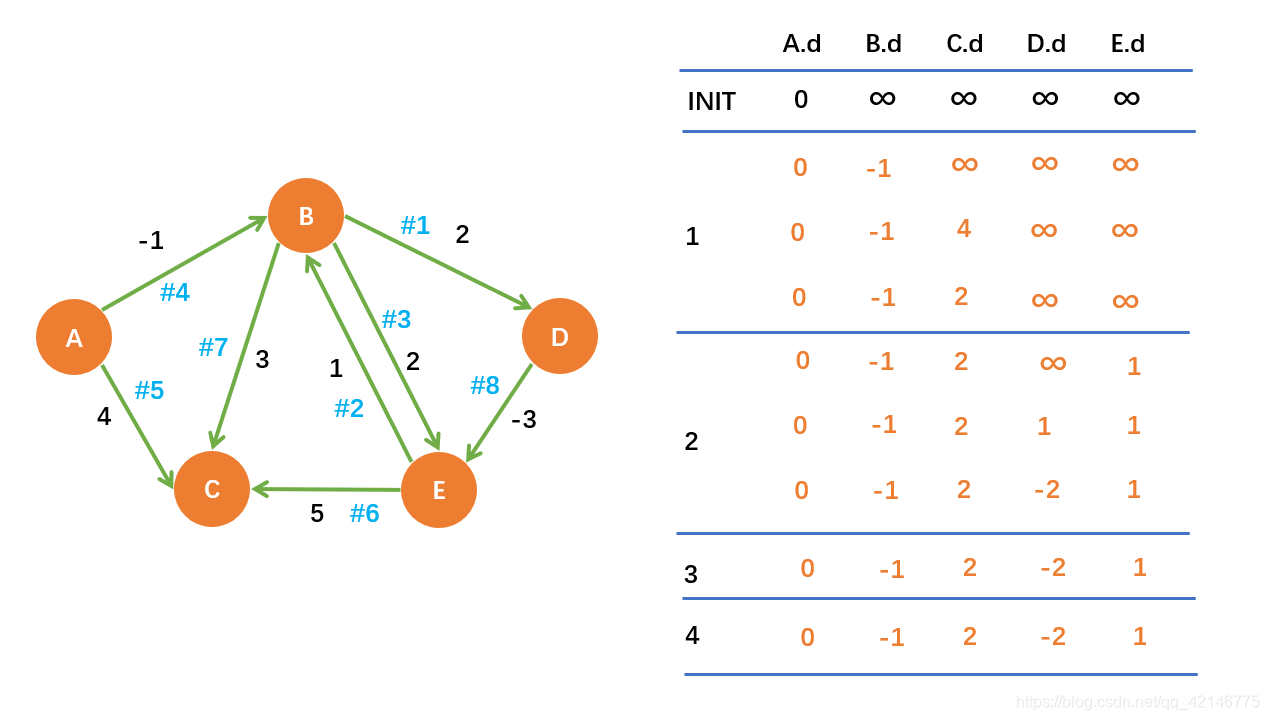
也就是我们假设s->u->…->v w为最短路径,按照s~>v最短路径边依次序进行松弛,最后v.d=δ(s,v)
证明:根据路径松弛性质,很容易证明正确性

因为即使是最坏的情况,如图1,每一轮对所有边进行松弛只得到一个点的最短路径,那么|V|-1轮,肯定|V|个结点都能得到,何况更好的情况,如图2

负权环判定
因为负权环可以无限制的降低总花费,所以如果发现第 n次操作仍可降低花销,就一定存在负权环
五丶SPFA
SPFA算法的基本思路与贝尔曼-福特算法相同,即每个节点都被用作用于松弛其相邻节点的备选节点。相较于贝尔曼-福特算法,SPFA算法的提升在于它并不盲目尝试所有节点,而是维护一个备选节点队列,并且仅有节点被松弛后才会放入队列中。整个流程不断重复直至没有节点可以被松弛。
SPFA(G,W,s)
{
init_single_source(G,s)
Q.push(v);
while(Q not empty){
u=pop(v)
foreach((u,v)∈G.E)
Relax(u,v,w) //需要将Relax加一句
}
foreach((u,v)∈G.E) //n次操作仍可降低花销,就一定存在负权环
if(v.d>u.d+w(u,v))
say("error")
}
//这里Relax有一些其余操作使用优先队列需要
Relax(u,v,w)
{
if(v.d>u.d+w(u,v))
{
v.d=u.d+w(u,v)
v.path=u
if(v!∈Q) Q.push(u);
}
}
判断有无负环:
如果某个点进入队列的次数超过N次则存在负环
单源最短路径问题的父亲————差分约束系统(线性规划)【引用wiki】
是求解关于一组变数的特殊不等式组方法
求解差分约束系统,可以转化成图论的单源最短路径问题。观察 xj- xi≤bk ,会发现它类似最短路中的δ(s,v)≤δ(s,u)+w(u,v),δ(s,v)-δ(s,u)≤w(u,v)。因此,以每个变数Xi为结点,对于约束条件 xj- Xi≤bk,连接一条边 (i,j),边权为 bk。再增加一个原点S与所有定点相连,边权均为0。对这个图以s为原点运行Bellman-ford算法(或SPFA算法),最终d[i]即为一组可行解。

附属知识
三角不等式:δ(s,v)≤δ(s,u)+w(u,v)
证明引理1:(u,v)进行松弛操作后v.d≤u.d+w(u,v)
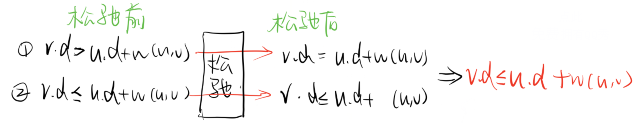
证明上界引理:任意次松弛操作v.d≥δ(s,v)且v.d=δ(s,v)后不会变小

证明收敛性质:s~>u->v是一条最短路径,如果送至(u,v)之前有u.d=δ(s,u),那么松弛(u,v)之后有v.d=δ(s,v)