二维向量
向量不代表位置 里面的元素只有两个 长度和方向 所以一个向量移动到其他位置 则这个向量没有发生变化 向量是可以平移的有向线段
一个向量的坐标等于表示这个向量的有向线段的终点坐标减去始点坐标的值 有向线段不管移动到哪里 只要方向和长度不变 最后运算得出的坐标都不变
加法
向量的四边形法则

根据图中的定律可以求出两个向量中间方向的向量
这有时在c#里面计算需要
向量的加法也可以表示为 下图所示的三角形法则

两张图其实一样
减法

OA-OB=BA.即“共同起点,指向被减”
OA - OB 可以理解为 OA + (-OB) 这时通过向量加法的法则也能得出减法法则一样的结果
向量的长度

将向量的起点与二维坐标系的原点对应
则向量与横坐标的夹角称为Θ
sinΘ = y / 向量的模
cosΘ = x /向量的模
向量的点乘
公式
a * b = |a| * |b| * cosθ θ 是a向量与b向量起点相连的夹角
意义 :|b| * cosθ 可以表示b投影到a向量的长度(不理解可以想象一下 直角三角形斜边与直角边a的关系,设他们的夹角为γ 斜边*cosγ则表示为直角边a了)
因为 |a| 和|b|都是大于0的,所以结果的正负值取决于 cosθ
所以 点乘结果小于0 参与点乘的两个向量的起点相连的夹角是钝角
大于0 则是锐角
等于0 则是直角
点乘的公式也可以表示为:
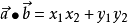
其中a = (x1, y1), b = (x2, y2)
点乘符合交换律
向量的叉乘
向量的叉乘结果是一个新向量
设向量a和b和叉乘结果向量c ,a与b的起点相连,夹角为θ
aXb=c
性质:
c⊥a,c⊥b,即结果向量垂直于叉乘向量组成的平面,无论是对于二维向量还是三维向量这一结论都成立
结果向量的模长:
|c| = |aXb|=|a||b|sinθ
向量的变换法则:
aXb=-bXa
两个向量叉乘的结果的模等于这两个向量和两个向量的平移向量围成的平行四边形的面积
|aXb|=|a||b|sinθ中|b|sinθ等于平行四边形的高,平行四边形的面积的底乘以高
特别需要注意的是叉乘结果的向量到底是垂直于ab所在平面的哪一面
二维向量的方向判定采取右手定则
在aXb=c中
右手四指并拢,从第一个叉乘向量a开始转动到第二个叉乘向量b
大拇指所指的方向表示的就是c的方向了
单位向量
单位向量是长度为1的向量
某个向量的单位向量(x,y)
长度为a
则其单位向量为(x / a, y / a)
二维坐标系
坐标系很基础这里就不解释了 稍微提一下
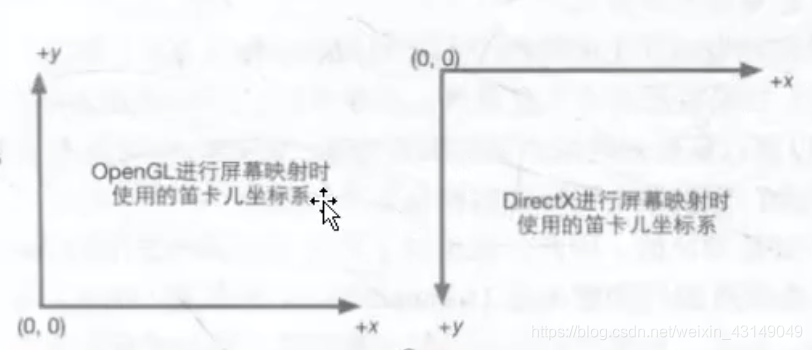
openGL里面的坐标系和DirectX里面的 坐标系是不一样的 DX 和 OG的坐标系可以互相转换,转换过程是旋转180度再进行水平翻转
二维坐标系的旋转
假设从xoy坐标系逆时针旋转到x`oy`坐标系
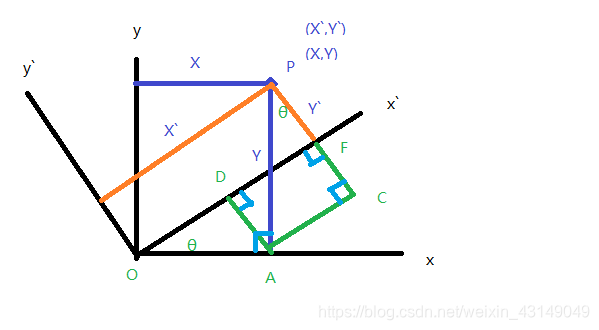
旋转角度为θ
图中的绿色线条是辅助线
很容易推断出另一个图中另一个θ角的存在
已知P在xoy的坐标(x,y)
需要推断出P在另一个坐标系中的位置
x` = OF = OD + DF
OD = OA * cosθ = x * cosθ
AC = PA * sinθ = y * sinθ
x` = x * cosθ + y * sinθ
y` = PC - FC
PC = PA * cosθ = y * cosθ
FC = OA * sinθ = x * sinθ
y` = y * cosθ - x * sinθ
所以旋转后的坐标系 x`oy`
P点的坐标是( x * cosθ + y * sinθ, y * cosθ - x * sinθ)
假设从xoy坐标系顺时针旋转到x`oy`坐标系
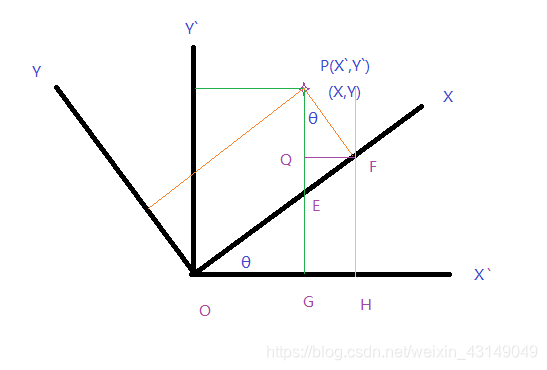
前置知识:
sin(-a)=-sin a
cos(-a)=cos a
tan a = sin a / cos a
sin ^ 2 θ + cos ^ 2 θ = 1
推理过程:
x` = OH - GH
OH = x * cos θ
GH = QF = y * sin θ
x` = x * cos θ - y * sin θ = x * cos (-θ) + y * sin (-θ)
x` = PE + EG
PE = y / cos θ
EG = OG * tan θ = x` * tan θ
y` = y / cos θ + (x * cos θ - y * sin θ) * sin θ / cos θ =
y / cos θ + x * sin θ - y sin ^ 2 θ / cos θ =
x * sin θ + (1 - sin ^ 2 θ) * y / cos θ =
x * sin θ + y * cos θ =
y * cos (-θ) - x * sin (-θ)
P点的坐标是(x * cos (-θ) + y * sin (-θ), y * cos (-θ) - x * sin (-θ))
坐标系顺时针旋转,原来的点在新坐标中的坐标是
( x * cosθ + y * sinθ, y * cosθ - x * sinθ)
坐标系逆时针旋转,原来的点在新坐标中的坐标是
(x * cos (-θ) + y * sin (-θ), y * cos (-θ) - x * sin (-θ))
可以发现 θ的符号 和旋转方向有关
不难证明,坐标系以原点为圆心以某个方向旋转某个角度后某个点的坐标,相当于原坐标系不动,这个点以原点为圆心以相反的方向旋转相同的角度后的坐标,虽然在实际运算的时候根据这个规律可以互相变换运算效果来更简便的得出点的新坐标, 但是因为两种方法的坐标系的不同,其实旋转坐标系与反方向旋转点得出的实际位置是不一样的
二维坐标系的平移
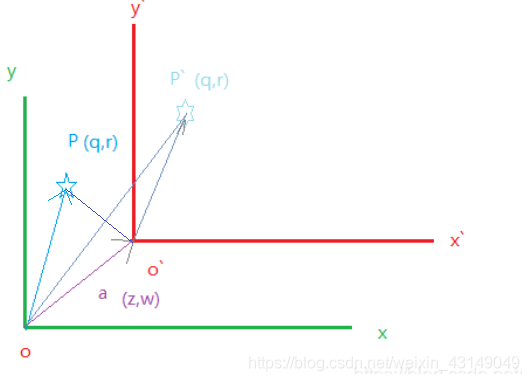
在xoy坐标系移动到x`oy`后
P`的位置在新的坐标系中的位置和
P在旧坐标系中的位置一样
求出P`在旧坐标系中的的位置OP`
根据向量的加法法则即可求出
求P在新坐标中的位置则使用向量的减法
二维坐标系的旋转和平移
求法是旋转和平移的复合
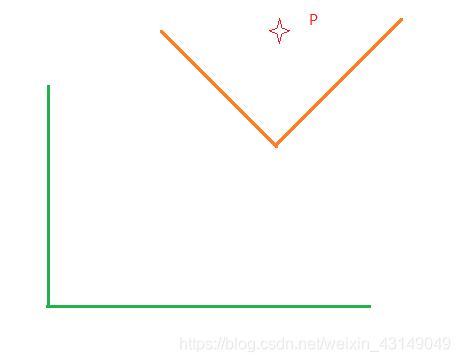
如图,求绿色坐标系中 P点的坐标
可以先将橙色坐标系旋转到绿色坐标系的角度
求出此时的P`点坐标
再将旋转后的橙色坐标平移到绿色坐标位置
求出此时的P``坐标即可
