Harris角点检测的目的是去分辨出图像中的平面、边界以及角点。
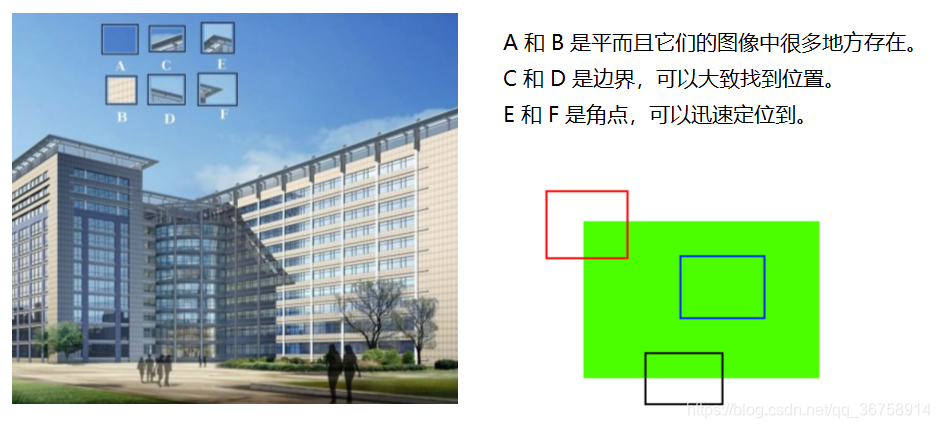
基本原理
下面三张图分别代表平面、边缘以及角点。
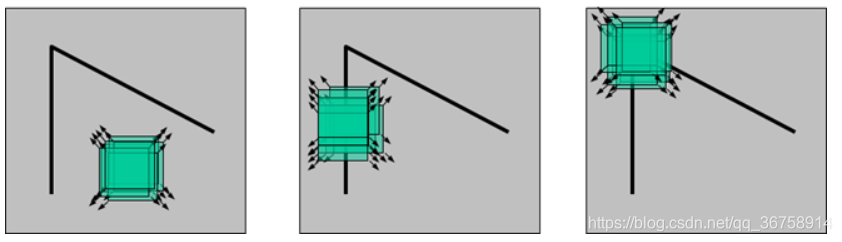 人眼对角点的识别通常是在一个局部的小区域或小窗口完成的。如果在各个方向上移动这个特征的小窗口,窗口内区域的灰度发生了较大的变化,那么就认为在窗口内遇到了角点。如果这个特定的窗口在图像各个方向上移动时,窗口内图像的灰度没有发生变化,那么窗口内的图像就可能是一个平面;如果窗口在某一个方向移动时,窗口内图像的灰度发生了较大的变化,而在另一些方向上没有发生变化,那么,窗口内的图像可能就是一条直线的线段。
人眼对角点的识别通常是在一个局部的小区域或小窗口完成的。如果在各个方向上移动这个特征的小窗口,窗口内区域的灰度发生了较大的变化,那么就认为在窗口内遇到了角点。如果这个特定的窗口在图像各个方向上移动时,窗口内图像的灰度没有发生变化,那么窗口内的图像就可能是一个平面;如果窗口在某一个方向移动时,窗口内图像的灰度发生了较大的变化,而在另一些方向上没有发生变化,那么,窗口内的图像可能就是一条直线的线段。
对于图像
I(x,y),当点
(x,y)平移了
(Δx,Δy)之后,其自适应性为:
c(x,y;Δx,Δy)=(u,v)∈W(x,y)∑ω(u,v)(I(u,v)−I(u+Δx,v+Δy))2
其中
W(x,y)是以点
(x,y)为中心的窗口,通常取
3×3的窗口尺寸,
ω(u,v)是此窗口上对应的每个点
(u,v)的权重,可以是常数,也可以是高斯加权函数。
将
I(u+Δx,v+Δy)进行一阶泰勒展开,得到:
I(u+Δx,v+Δy)=I(u,v)+Iu(u,v)Δx+Iv(u,v)Δy+O(Δx2,Δy2)≈I(u,v)+Iu(u,v)Δx+Iv(u,v)Δy
近似可得:
c(x,y;Δx,Δy)=(u,v)∈W(x,y)∑ω(u,v)(Iu(u,v)Δx+Iv(u,v)Δy)2
因为根据二次型转换,有:
c(x,y;Δx,Δy)=[ΔxΔy]M(u,v)[ΔxΔy]
其中,
M(u,v)=(u,v)∈W(x,y)∑ω(u,v)[Iu(u,v)2Iu(u,v)Iv(u,v)Iu(u,v)Iv(u,v)Iv(u,v)2]=⎣⎢⎡(u,v)∈W(x,y)∑ω(u,v)Iu(u,v)2(u,v)∈W(x,y)∑ω(u,v)Iu(u,v)Iv(u,v)(u,v)∈W(x,y)∑ω(u,v)Iu(u,v)Iv(u,v)(u,v)∈W(x,y)∑ω(u,v)Iv(u,v)2⎦⎥⎤=[ACCB]
将
[ACCB]对角化过后,会得到:
[ACCB]=R−1[λ100λ2]R
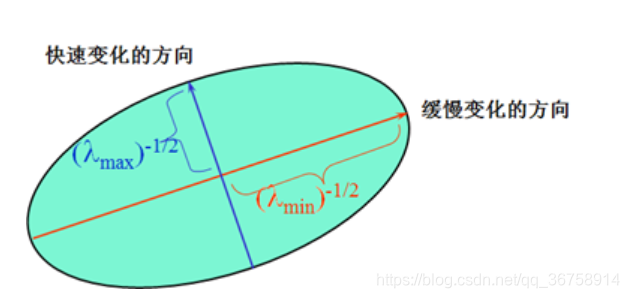
由于忽略余项之后的表达式为一个二项式函数,然而二项式函数的本质上就是一个椭圆函数,椭圆的扁率和尺寸是由M(x,y)的特征值λ1、λ2决定的,椭圆的方向是由M(x,y)的特征矢量决定的,如下图所示,椭圆方程为:
[ΔxΔy]M(x,y)[ΔxΔy]=1
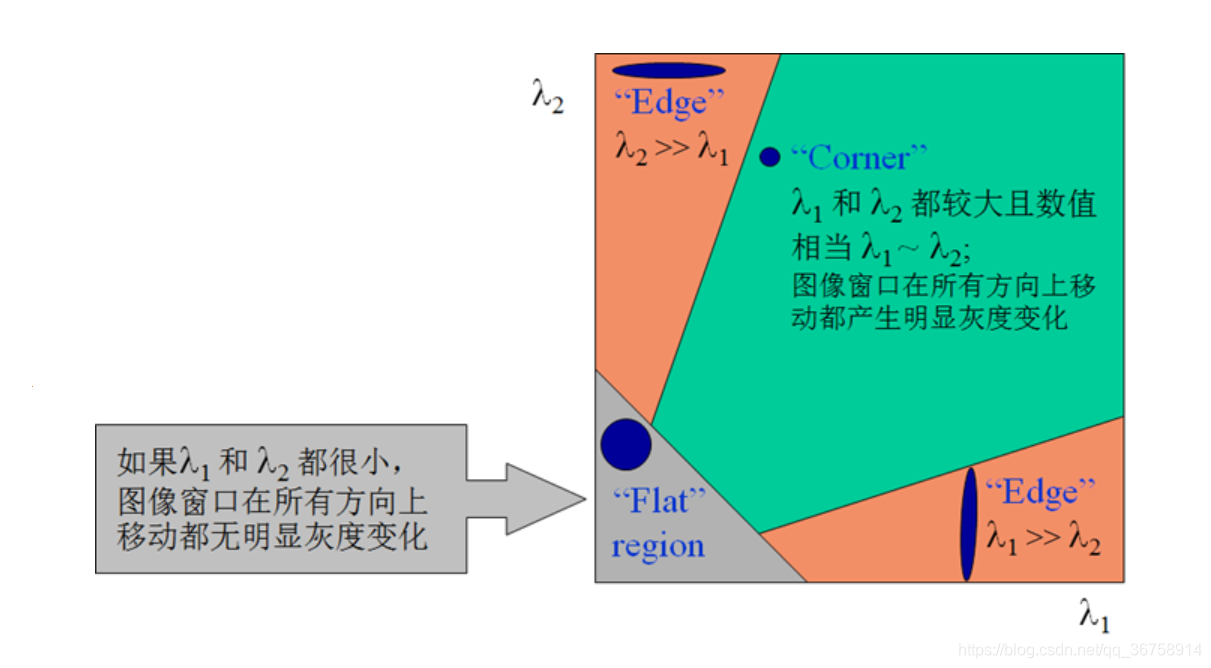
 椭圆函数特征值与图像中的角点、直线(边缘)和平面之间的关系如下图所示。共可分为三种情况:
椭圆函数特征值与图像中的角点、直线(边缘)和平面之间的关系如下图所示。共可分为三种情况:
a. 图像中的直线。一个特征值大,另一个特征值小,λ1>λ2或λ2>λ1。自相关函数值在某一方向上大,在其他方向上小。
b. 图像中的平面。两个特征值都小,且近似相等;自相关函数数值在各个方向上都小。
c. 图像中的角点。两个特征值都大,且近似相等,自相关函数在所有方向都增大。
 由于我们是通过M的两个特征值的大小对图像进行分类,所以,定义角点响应R值:
由于我们是通过M的两个特征值的大小对图像进行分类,所以,定义角点响应R值:
R=detM−α(traceM)
其中,
detM=λ1λ2以及
traceM=λ1+λ2
所以,上图可以转化为:
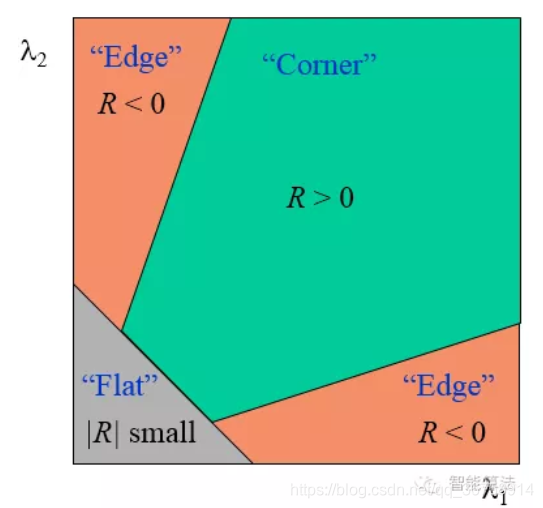
用python实现Harris角点检测
import cv2
import numpy as np
img = cv2.imread('box.png')
print ('img.shape:',img.shape)
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
dst = cv2.cornerHarris(gray, 2, 3, 0.04)
print ('dst.shape:',dst.shape)
img[dst>0.1*dst.max()]=[0,0,255]
cv2.imshow('dst',img)
cv2.waitKey(0)
cv2.destroyAllWindows()
得到的结果为:
原图像:

标出角点后的图像:


 人眼对角点的识别通常是在一个局部的小区域或小窗口完成的。如果在各个方向上移动这个特征的小窗口,窗口内区域的灰度发生了较大的变化,那么就认为在窗口内遇到了角点。如果这个特定的窗口在图像各个方向上移动时,窗口内图像的灰度没有发生变化,那么窗口内的图像就可能是一个平面;如果窗口在某一个方向移动时,窗口内图像的灰度发生了较大的变化,而在另一些方向上没有发生变化,那么,窗口内的图像可能就是一条直线的线段。
人眼对角点的识别通常是在一个局部的小区域或小窗口完成的。如果在各个方向上移动这个特征的小窗口,窗口内区域的灰度发生了较大的变化,那么就认为在窗口内遇到了角点。如果这个特定的窗口在图像各个方向上移动时,窗口内图像的灰度没有发生变化,那么窗口内的图像就可能是一个平面;如果窗口在某一个方向移动时,窗口内图像的灰度发生了较大的变化,而在另一些方向上没有发生变化,那么,窗口内的图像可能就是一条直线的线段。 椭圆函数特征值与图像中的角点、直线(边缘)和平面之间的关系如下图所示。共可分为三种情况:
椭圆函数特征值与图像中的角点、直线(边缘)和平面之间的关系如下图所示。共可分为三种情况: 由于我们是通过M的两个特征值的大小对图像进行分类,所以,定义角点响应R值:
由于我们是通过M的两个特征值的大小对图像进行分类,所以,定义角点响应R值:


