机器学习：向量空间中的投影

今天介绍向量空间中的投影，以及投影矩阵。
假设空间中有两个向量 $\mathbf{a}, \mathbf{b}$， $\mathbf{b}$ 在 $\mathbf{a}$ 上的投影为 $\mathbf{p}$，我们要计算出 $\mathbf{p}$ 到底是多少，如下图所示：

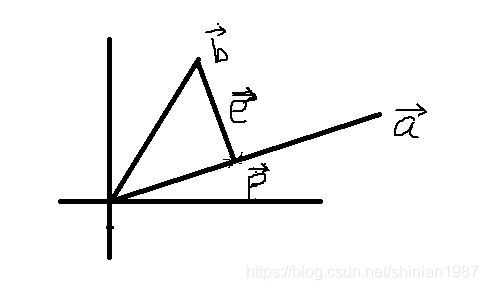
为了计算 $\mathbf{p}$，我们可以先假设 $\mathbf{p} = x \mathbf{a}$，因为 $\mathbf{p}$ 是在 $\mathbf{a}$ 上，所以两者只差系数的关系，如上图所示，我们可以找到 $\mathbf{b}$ 和 $\mathbf{p}$ 的差： $\mathbf{e} = \mathbf{b} - \mathbf{p} = \mathbf{b} - x\mathbf{a}$，而我们又可以看出， $\mathbf{e}$ 是和 $\mathbf{a}$ 垂直的，所以 $\mathbf{e} \cdot \mathbf{a} = \mathbf{a}^{T} \mathbf{e} = 0$，我们可以进一步得到，

$\mathbf{a}^{T}(\mathbf{b} - x\mathbf{a})=0$
所以：
$\mathbf{a}^{T}\mathbf{b} -x\mathbf{a}^{T}\mathbf{a} =0$
进而：
$x = \frac{\mathbf{a}^{T}\mathbf{b}}{\mathbf{a}^{T}\mathbf{a}}$
所以：

$\mathbf{p} = x \mathbf{a} = \frac{\mathbf{a}\mathbf{a}^{T}}{\mathbf{a}^{T}\mathbf{a}}\mathbf{b}$

所以投影矩阵
$\mathbf{P} = \frac{\mathbf{a}\mathbf{a}^{T}}{\mathbf{a}^{T}\mathbf{a}}$

这是到直线的投影，如果是到矩阵的投影，我们也可以用类似的方法求得, 只是将上面的向量 $\mathbf{a}$ 换成矩阵 $\mathbf{A}$ ，假设向量 $\mathbf{b}$ 在矩阵 $\mathbf{A}$ 上的投影为 $\mathbf{A}\mathbf{x}$，相当于向量 $\mathbf{b}$ 投影到了矩阵 $\mathbf{A}$ 的列空间上，而矩阵 $\mathbf{A}$ 的列空间与其 left-null 空间是互相垂直的，所以：

$\mathbf{A}^{T}(\mathbf{b} - \mathbf{A}\mathbf{x})=0$
所以：
$\mathbf{A}^{T}\mathbf{b} -\mathbf{A}^{T}\mathbf{A}\mathbf{x} =0$
进而：
$\mathbf{x} = (\mathbf{A}^{T}\mathbf{A})^{-1} \mathbf{A}^{T}\mathbf{b}$
所以：

$\mathbf{p} = \mathbf{A} \mathbf{x}= \mathbf{A} (\mathbf{A}^{T}\mathbf{A})^{-1} \mathbf{A}^{T}\mathbf{b}$

所以投影矩阵
$\mathbf{P} = \mathbf{A} (\mathbf{A}^{T}\mathbf{A})^{-1} \mathbf{A}^{T}$

关于投影，最后多说几句，讲讲点到直线的距离，这个与机器学习中的 SVM 的最初的优化函数有关：

扫描二维码关注公众号，回复： 8630072 查看本文章

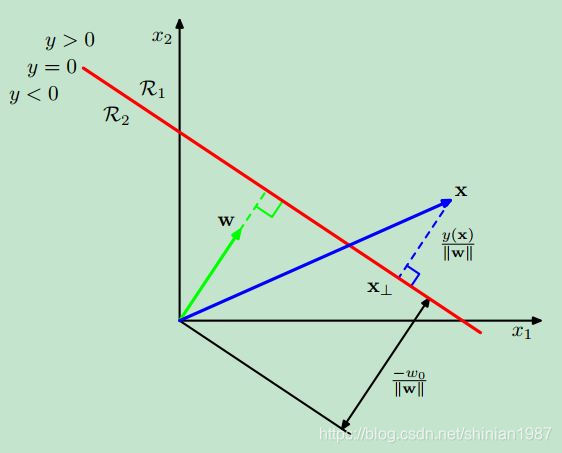
这个图是那本经典的机器学习教材 《Pattern Recognition and Machine Learning》里的，这个是想说明向量空间中，一个点到直线的距离。假设直线的表达式为 $f(\mathbf{x})=\mathbf{w}^{T}\mathbf{x}+w_0$，如果我们要求一个点 $\mathbf{x}$ 到该直线的距离，我们可以用上面说的投影来求这个距离, 假设点 $\mathbf{x}$ 到直线上的投影为 $\mathbf{x}_{\perp}$，如上图的 $\mathbf{x}_{\perp}$，而 $\mathbf{x}_{\perp}$ 到 $\mathbf{x}_{\perp}$ 的这个向量与 $\mathbf{w}$ 是平行的，所以我们可以得到如下的表达式：

$\mathbf{x} = \mathbf{x}_{\perp} + r \frac{\mathbf{w}}{||\mathbf{w}||}$

两边同时乘以 $\mathbf{w}$ 并且加上 $w_0$， 可以得到：

$\mathbf{w}^{T}\mathbf{x} + w_0 = \mathbf{w}^{T}\mathbf{x}_{\perp} + w_0 + r \frac{\mathbf{w}^{T}\mathbf{w}}{||\mathbf{w}||}$

因为 $\mathbf{x}_{\perp}$ 在直线上，所以 $\mathbf{w}^{T}\mathbf{x}_{\perp} + w_0 = 0$，进而，我们可以得到：

$f(\mathbf{x}) = r ||\mathbf{w}|| \Rightarrow r = \frac{f(\mathbf{x})}{||\mathbf{w}||}$

因为 $\frac{\mathbf{w}}{||\mathbf{w}||}$ 是单位向量，所以这个向量的幅值就是 $r$，所以点 $\mathbf{x}$ 到该直线的距离就是 $r$。这个距离的表达式，就是机器学习里 SVM 的基础，SVM 要优化的就是寻找这样一个 $\mathbf{w}$ 使得所有离该直线最近的点的距离最远，听起来好像有点绕哈~