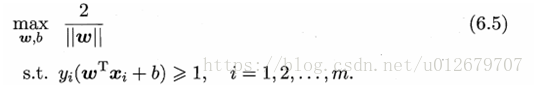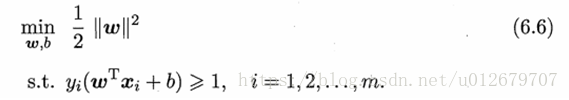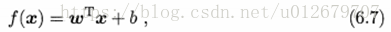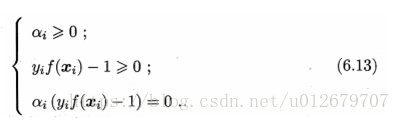【机器学习】支持向量机
1.分类超平面与最大间隔
2.对偶问题与拉格朗日乘子法
3.核函数
4.软间隔与正则化
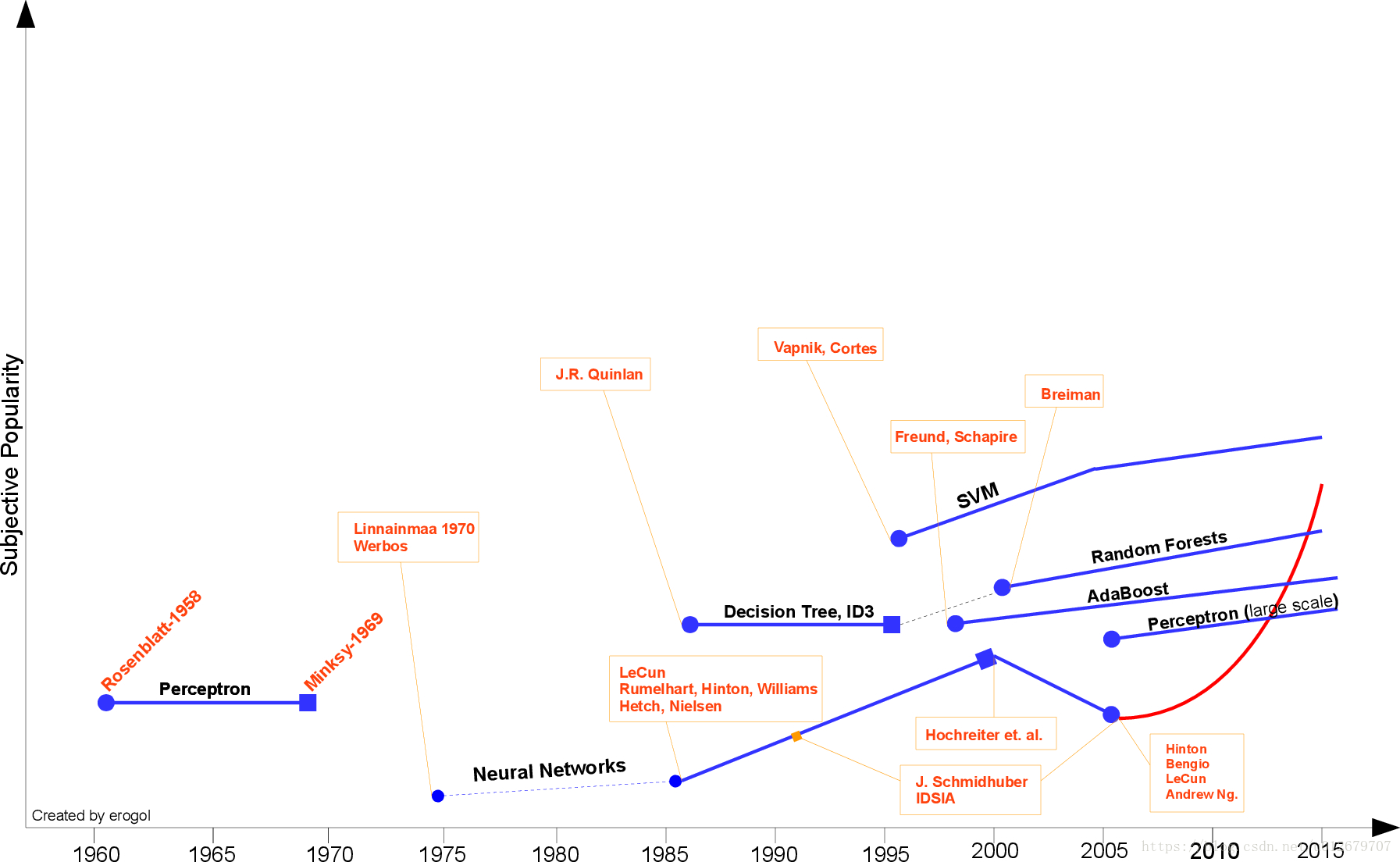
上图是一个关于机器学习算法的时间线来自于Eren Golge。可以看出SVM旺盛的生命力。实际上,即使是深度学习非常火热的今天,SVM依然盛行。在一些小样本分类问题上,SVM表现非常好,用深度学习模型可能反而会使问题变得更复杂。
下面开始介绍SVM--支持向量机。
1.分类超平面与最大间隔
给定训练样本集 D ={ (X1 ,Yl),(X2,Y2)..., (Xm,Ym)}, Yi ∈{-1,+1},分类学习最基本的想法就是基于训练集D在样本空间中找到一个划分超平面、将不同类别的样本分开。
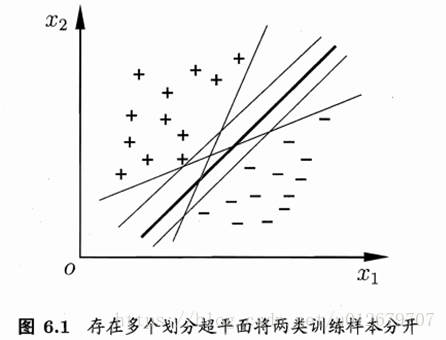
但能将训练样本分开的划分超平面可能有很多,如图 6.1所示,我们应该努力去找到哪一个昵?
原则上,是去找位于两类训练样本"正中间"的划分超平面,即图 6.1中黑色最粗的那个,因为该划分超平面对训练样本局部扰动的"容忍性“最好,鲁棒性最强,泛化能力最强。
例如,由于训练集的局限性或噪声的因素,训练集外的样本可能比图6.1中的训练样本更接近两个类的分隔界,这将使许多划分超平面出现错误,而黑色最粗的那个超平面受影响最小。换言之,这个划分超平面所产生的分类结果是最鲁棒的,对未见示例的泛化能力最强。
在样本空间中,划分超平面可通过如下线性方程来描述:
其中:
x=(x1,x2…xd)为输入数据,维度为d。

b为位移项,决定了超平面与原点之间的距离。
显然,分类超平面可被法向量ω和位移b确定,下面我们将其记为(w,b)。样本空间中任意点 x到超平面(w,b)的距离可写为:
点到超平面的距离,可参考点到直线的距离公式,见附录【1】。
假设超平面(w,b)能将训练样本正确分类,即对于
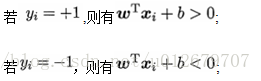
所以,令:
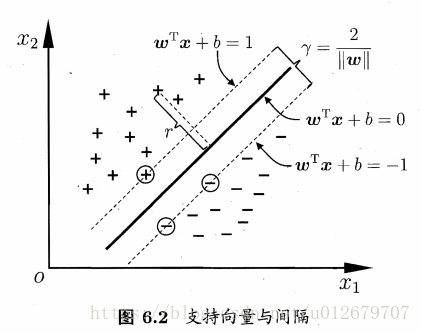
如图6.2所示,距离超平面最近的这几个训练样本点使式(6.3)的等号成立,它们被称为"支持向量",两个异类支持向量到超平面的距离之和为:
其中,γ被称为"间隔"。
那如何找到具有“最大间隔”的分类超平面呢?
欲找到具有"最大间隔" (maximum margin) 的划分超平面,也就是要找到能满足式(6.3)中约束的参数w和b,使得γ最大,即
显然,为了最大化间隔γ,仅需最小化||w||。于是,式(6.5)可重写为:
上述(6.6)是支持向量机的基本型。
支持向量机有何特点?
支持向量满足:
最大化间隔真的仅与ω有关吗?
NO!事实上,最大化间隔不只与ω有关,偏置b通过约束隐性地影响着w的取值,进而对间隔产生影响。
为什么目标函数要写成(6.6)中的凸函数形式呢?
在表示最大化间隔的优化问题中,发现式(6.5)中的目标函数是非凸的,并没有现成的可用的软件来解决非凸函数的优化问题。所以改成了(6.6)中的凸函数形式。
关于凸函数,可见附录【2】。
2.对偶问题与拉格朗日乘子法
我们希望求解式(6.6)来得到最大间隔分类超平面所对应的模型f(x):
其中ω和b是模型参数。注意到式(6.6)本身是一个凸二次规划问题,能直接用现成的优化计算包求解,但我们可以有更高效的办法。
对式(6.6)使用拉格朗日乘子法可得到其"对偶问题" 。具体来说,对式(6.6)的每条约束添加拉格朗日乘子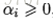
从对偶问题(6.11)解出的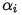

于是,对任意训练样本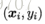
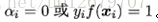
若
若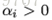

这显示出支持向量机的一个重要性质:训练完成后,大部分的训练样本都不需保留,最终模型仅与支持向量有关。
那么如何求解式(6.11) 呢?不难发现,这是一个二次规划问题?可使用通用的二次规划算法来求解,二次规划可见附录【3】。这里我还没搞懂,先留着坑。
3.核函数
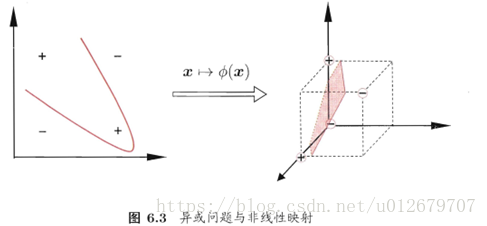
在本章前面的讨论中,我们假设训练样本是线性可分的,即存在一个划分超平面能将训练样本正确分类。然而在现实任务中,原始样本空间内,也许并不存在一个能正确划分两类样本的超平面。例如图 6.3 中的" 异或 " 问题就不是线性可分的。
那如何解决非线性可分问题呢?
对于原空间中的非线性可分问题,可将样本从原始空间映射到一个更高维的特征空间,使得样本在这个特征空间内线性可分。例如在图6.3中,若将原始的二维空间映射到一个合适的三维空间 ,就能找到一个合适的划分超平面。幸运的是,如果原始空间是有限维,即属性数有限,那么一定存在一个高维特征空间使样本可分。
这里的函数 κ(.,.)就是"核函数"。式(6.24)显示出模型最优解可通过训练样本的核函数展开,这一展式亦称"支持向量展式 "显然,若己知合适映射Ф的具体形式,则可写出核函数 κ(.,.)。但在现实任务中我们通常不知道Ф是什么形式,那么,合适的核函数是否一定存在呢?什么样的函数能做核函数呢?
我们有下面的定理:
那核函数的特点是什么?
核函数:一个对称函数所对应的核矩阵半正定,它就可作为核函数使用。
事实上,对于一个半正定核矩阵,总能找到一个与之对应的映射Ф。换言之,任何一个核函数都隐式地定义了一个称为"再生核希尔伯特空间"的特征空间。
通过前面的讨论可知,我们希望样本在特征空间内线性可分,因此特征空间的好坏对支持向量机的性能至关重要。需注意的是,在不知道特征映射的形式时,我们并不知道什么样的核函数是合适的,而核函数也仅是隐式地定义了这个特征空间。于是,"核函数选择"成为支持向量机的最大变数。若核函数选择不合适,则意味着将样本映射到了一个不合适的特征空间,很可能导致性能不佳。
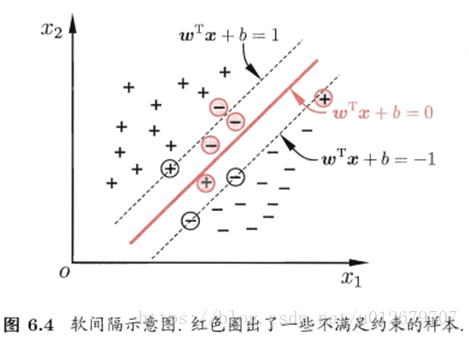
4.软间隔与正则化
在前面的讨论中,我们一直假定训练样本在样本空间或特征空间中是线性可分的,即存在一个超平面能将不同类的样本完全划分开。然而,在现实任务中往往很难确定合适的核函数使得训练样本在特征空间中线性可分。
退一步说,即使恰好找到了某个核函数使训练集在特征空间中线性可分,也很难断定这个貌似线性可分的结果不是由于过拟合所造成的。
那么如何缓解该问题呢?
缓解该问题的一个办法是:允许支持向量机在一些样本上出错。为此,引入"软间隔"的概念,如图 6.4所示:
具体来说,前面介绍的支持向量机是要求所有样本均满足约束(6.3),即所有样本都必须划分正确,这称为"硬间隔" ,而软间隔则是允许某些样本不满足约束:
------------------------------------------------------- 附录 ----------------------------------------------
附录【1】:
注意: ||w||是指欧几里得范数,例,w=(w1,w2,…wn)的转置, ||w||的求解如下:
所以,
附录【2】
凸函数:
在凸集中任取两个点连成一条直线,这条直线上的点仍然在这个集合内部,如下图的左图。
优点:凸函数局部最优就是全局最优,而右边的非凸函数的局部最优就不是全局最优了。
(左为凸函数,右为非凸函数)
附录【3】
二次规划
二次规划(Quadratic Programming,简称 QP)是一类典型的优化问题,包括凸二次优化和非凸二次优化。在此类问题中,目标函数是变量的二次函数,而约束条件是变量的线性不等式。
假定变量个数为d,约束条件的个数为m,则标准的二次规划问题形如:
其中m为d维向量,为实对称矩阵,为实矩阵,和为实向量,Ax≤b的每一行对应一个约束。
可能的情况有:
(1)若Q为半正定矩阵,则式(B.12)目标函数是凸函数,相应的二次规划是凸二次优化问题,此时若约束条件Ax≤b定义的可行域不为空,且目标函数在此可行域有下界,则该问题将有全局最小值。
(2)若Q为正定矩阵,则该问题有唯一的全局最小值。
(3)若Q为非正定矩阵,则式(B.12)是有多个平稳点和局部极小点的NP难问题。
常用的二次规划解法有椭球法(ellipsoid method)、内点法(interior point)、增广拉格朗日法 (augmented Lagrangian) 、梯度投影法 (gradient projeetion) 等。若Q为正定矩阵,则相应的二次规划问题可由椭球法在多项式时间内求解。
注意:
非标准二次规划问题中可以包含等式约束,注意到等式约束能用两个不等式约束来代替;不等式约束可通过增加松弛变量的方式转化为等式约束。
------------------------------------------- END -------------------------------------
参考:
周志华《机器学习》
SVM-支持向量机原理详解与实践 https://www.cnblogs.com/spoorer/p/6551220.html