《土豆笔记之反向求导细节系列》Conv卷积层的反向求导细节

前言

这个系列主要是对深度学习中常见的各种层的反向求导细节进行学习和介绍，并且辅以代码予以理解，本章介绍的是卷积层，考虑到不同通道之间的转换并且不同的stride，padding等，卷积层的反向求导研究起来也是颇有意思的。如有谬误请联系指出，谢谢。

联系方式：
e-mail: [email protected]
QQ: 973926198
github: https://github.com/FesianXu

卷积层的前向传播和反向传播

我们对卷积层可谓是既熟悉又陌生，熟悉在于我们在深度学习中基本上每个模型都采用了卷积层，陌生在于很多人被问及卷积层的反向求导过程时，总是不能很好地回答出来，我们在本文中尝试对其进行探索，我们首先从卷积层的前向传播开始看起，注意到在深度学习中，卷积操作相当于信号学中的相关操作，也就是不存在卷积核的水平翻转这一步操作。一般来说，我们用公式(1.1)表示卷积操作，本文都以2D卷积作为例子，其他维度的卷积原理一致。
$\mathbf{y} = \mathbf{w} \star \mathbf{x} \tag{1.1}$
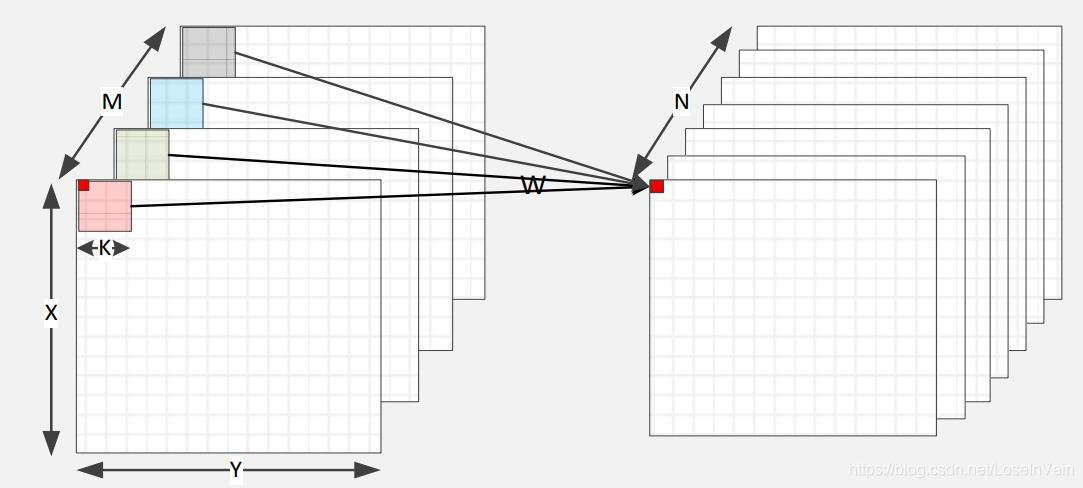
如果用C++语言形式的代码进行描述的话，如下所示，图示如Fig 1。

for (int n = 0; n < N; n++){                      // 输出通道数
    for (int m = 0; m < M; m++) {                 // 输入通道数
        for (int y = 0; y < Y; y++) {             // 输入图像的width
            for (int x = 0; x < X; x++) {         // 输出图像的height
                for (int p = 0; p < K; p++){      // 卷积核大小K
                    for (int q = 0; q < K; q++){  // 卷积核大小K
                        y_L[n,x,y] += y_L_1[m,x+p,y+q] * w[n,m,p,q];
                    }
                }
            }
        }
    }
}

在这里插入图片描述

Fig 1. 卷积操作的图示。

当然，以上的代码是没有考虑padding和不同的stride的，如果考虑上，代码形式将会变得更加复杂。不过我们能够发现，就卷积层这一层的反向传播而言，其导数为
$\dfrac{\partial E}{\partial w[n,m,p,q]} = \dfrac{\partial E}{\partial y_L} * \dfrac{\partial y_L}{\partial w[n,m,p,q]} \tag{1.2}$

$\dfrac{\partial y_L}{\partial w[n,m,p,q]} = \sum_{x,y} (y_{L-1}[m,x+p,y+q]) \tag{1.3}$

只是与输入图像的每个像素值有关而言（如果进行了padding，则和填充值也有关系。），我们接下来观察下具体体现到代码上会是什么关系。

我们首先先不考虑padding的影响。

我们用pytorch代码：

import torch 
import torch.nn as nn
import numpy as np
conv = nn.Conv2d(in_channels=1, out_channels=1, kernel_size=3, padding=0, bias=False,stride=1)
padding = nn.ConstantPad2d(0, 0)
inputv = torch.range(1,16).view(1,1,4,4)
out = conv(inputv)
padded = padding(inputv)
print(padded)
print(out)
out = out.mean()
out.backward()
print(conv.weight.grad)

输出的padded和out结果如

tensor([[[[ 1.,  2.,  3.,  4.],
          [ 5.,  6.,  7.,  8.],
          [ 9., 10., 11., 12.],
          [13., 14., 15., 16.]]]])
tensor([[[[4.8357, 5.8584],
          [8.9263, 9.9489]]]], grad_fn=<MkldnnConvolutionBackward>)

conv.weight.grad结果如

tensor([[[[ 3.5000,  4.5000,  5.5000],
          [ 7.5000,  8.5000,  9.5000],
          [11.5000, 12.5000, 13.5000]]]])

分析这个梯度的生成结果非常简单，我们只分析第一个参数w[0,0]的梯度。我们发现，在该实验的设置stride = 1, padding = 0的情况下，我们的第一个参数w[0,0]在划窗过程中，只会和输入的某些单元相乘，在这里是

tensor([[1., 2.],
        [5., 6.]])

因此求导结果也只是这些单元值的求和而已，我们用符号 $S_{i,j}$ 表示这个限定单元中的值，但是考虑到不同尺度的卷积核不应该导致求和结果尺度上的变化，我们对其进行标准化，如
$d = \dfrac{1}{T*T} \sum_{i,j} S_{i,j}\tag{1.4}$
在我们这个例子中，则是 $\dfrac{1}{4} (1+2+5+6) = 3.5$ ，结果和我们自动求导结果一致。对于参数矩阵中的其他值，其原理也是一样的。

在多通道输出（输入通道数为1，输出通道数为2）时，我们的代码变成了：

import torch 
import torch.nn as nn
import numpy as np
conv = nn.Conv2d(in_channels=1, out_channels=2, kernel_size=3, padding=0, bias=False,stride=1)
padding = nn.ConstantPad2d(0, 0)
inputv = torch.range(1,16).view(1,1,4,4)
out = conv(inputv)
padded = padding(inputv)
print(padded)
print(out)
out = out.mean()
out.backward()
print(conv.weight.grad)

输出结果为：

tensor([[[[ 1.,  2.,  3.,  4.],
          [ 5.,  6.,  7.,  8.],
          [ 9., 10., 11., 12.],
          [13., 14., 15., 16.]]]])
# padded
tensor([[[[ 1.3282,  1.5416],
          [ 2.1817,  2.3950]],

         [[-2.2801, -2.9749],
          [-5.0594, -5.7542]]]], grad_fn=<MkldnnConvolutionBackward>)
# out
tensor([[[[1.7500, 2.2500, 2.7500],
          [3.7500, 4.2500, 4.7500],
          [5.7500, 6.2500, 6.7500]]],


        [[[1.7500, 2.2500, 2.7500],
          [3.7500, 4.2500, 4.7500],
          [5.7500, 6.2500, 6.7500]]]])
# grad

我们发现我们的梯度现在变成了之前那个版本的“对半分”了。

再观察一个例子，这个时候，输入通道和输出通道数量变了，此时输入通道为2，输出通道为1

import torch 
import torch.nn as nn
import numpy as np
conv = nn.Conv2d(in_channels=2, out_channels=1, kernel_size=3, padding=0, bias=False,stride=1)
padding = nn.ConstantPad2d(0, 0)
inputv = torch.range(1,32).view(1,2,4,4)
out = conv(inputv)
padded = padding(inputv)
print(padded)
print(out)
out = out.mean()
out.backward()
conv.weight.grad

输出结果为：

tensor([[[[ 3.5000,  4.5000,  5.5000],
          [ 7.5000,  8.5000,  9.5000],
          [11.5000, 12.5000, 13.5000]],

         [[19.5000, 20.5000, 21.5000],
          [23.5000, 24.5000, 25.5000],
          [27.5000, 28.5000, 29.5000]]]])
# grad

再观察一个例子，此时输入通道为2，输出通道为2

import torch 
import torch.nn as nn
import numpy as np
conv = nn.Conv2d(in_channels=2, out_channels=2, kernel_size=3, padding=0, bias=False,stride=1)
padding = nn.ConstantPad2d(0, 0)
inputv = torch.range(1,32).view(1,2,4,4)
out = conv(inputv)
padded = padding(inputv)
print(padded)
print(out)
out = out.mean()
out.backward()
conv.weight.grad

输出结果为：

tensor([[[[ 1.7500,  2.2500,  2.7500],
          [ 3.7500,  4.2500,  4.7500],
          [ 5.7500,  6.2500,  6.7500]],

         [[ 9.7500, 10.2500, 10.7500],
          [11.7500, 12.2500, 12.7500],
          [13.7500, 14.2500, 14.7500]]],


        [[[ 1.7500,  2.2500,  2.7500],
          [ 3.7500,  4.2500,  4.7500],
          [ 5.7500,  6.2500,  6.7500]],

         [[ 9.7500, 10.2500, 10.7500],
          [11.7500, 12.2500, 12.7500],
          [13.7500, 14.2500, 14.7500]]]])
# grad

我们不难发现，输入通道数为2，输出通道数为2，又是输入通道数为2，输出通道数为1的“对半分”版本。但是与第一个输入通道数为1，输出通道数为1还是有所不同的，其输入通道数导致了其有两个不同的“梯度面”。

这个时候，我们应该这样理解，对于参数w和b的求导而言，我们只在乎其和输入图的哪些元素进行过乘法操作，不过如果输入图是多通道的时候，我们需要考虑输入图不同通道的影响。具体来说是这样的，

当输入通道数为1的时候，不管输出通道多少，其参数都只能和输入图的唯一通道的某些单元进行乘法操作，但是为了避免因为输出通道太多（比如1024个输出通道），导致整体尺度的变化，我们对于多输出通道的情况，需要对其进行输出通道数的标准化，也即是
$d = \dfrac{1}{C_{out} T *T} \sum_{i,j} S_{i,j}\tag{1.5}$
这个就是为什么会出现“对半分”的原因了。

当输入通道不为1时，我们在输入上需要初始化和输入通道数相同通道数的参数，比如w.shape = [c_in=2,c_out=1,w=3,h=3]等，同样只考虑参数和输入的某些单元进行的操作，我们同样能得到相同的结论，不过因为输入通道上没有进行划窗，某个参数比如w[0,0,0]只能和输入的某个通道上的某些单元进行操作，因此对于输入通道数不为一的情况而言，就不像多通道输出那样是相同的梯度图了，而是不同的梯度图。这里比较绕，也不容易说清楚，不过大家总是要记住一个原则只考虑某个参数和输入的某些单元进行了操作，取某些单元进行求和，也便得到了梯度。

如果我们考虑上padding的话呢？代码如下：

import torch 
import torch.nn as nn
import numpy as np
conv = nn.Conv2d(in_channels=1, out_channels=2, kernel_size=3, padding=1, bias=False,stride=1)
padding = nn.ConstantPad2d(1, 0)
inputv = torch.range(1,16).view(1,1,4,4)
out = conv(inputv)
padded = padding(inputv)
print(padded)
print(out)
out = out.mean()
out.backward()
conv.weight.grad

输出如：

tensor([[[[ 0.,  0.,  0.,  0.,  0.,  0.],
          [ 0.,  1.,  2.,  3.,  4.,  0.],
          [ 0.,  5.,  6.,  7.,  8.,  0.],
          [ 0.,  9., 10., 11., 12.,  0.],
          [ 0., 13., 14., 15., 16.,  0.],
          [ 0.,  0.,  0.,  0.,  0.,  0.]]]])
# padded
tensor([[[[  0.3218,  -0.5875,  -0.9161,  -1.0469],
          [  0.8760,  -1.3331,  -1.4916,  -2.7052],
          [  1.5649,  -1.9673,  -2.1258,  -4.3268],
          [  0.9981,  -1.4645,  -1.5532,  -5.2222]],

         [[ -1.0337,  -2.4976,  -3.1457,  -1.3275],
          [ -3.3036,  -5.8747,  -6.9092,  -2.9231],
          [ -5.9784, -10.0127, -11.0472,  -4.7044],
          [ -7.7863,  -9.7732, -10.5602,  -4.2805]]]],
       grad_fn=<MkldnnConvolutionBackward>)
# out
tensor([[[[1.6875, 2.4375, 1.9688],
          [3.0000, 4.2500, 3.3750],
          [2.8125, 3.9375, 3.0938]]],

        [[[1.6875, 2.4375, 1.9688],
          [3.0000, 4.2500, 3.3750],
          [2.8125, 3.9375, 3.0938]]]])
# grad

梯度结果也很容易理解，其实是对padding过后的输入进行了划窗操作，同样是只考虑与某个参数进行了操作的输入参数，比如w[0,0]显然是和输入

tensor([[ 0.,  0.,  0.,  0.],
        [ 0.,  1.,  2.,  3.],
        [ 0.,  5.,  6.,  7.],
        [ 0.,  9., 10., 11.]])

进行的操作，因此梯度为 $\dfrac{1}{2 * 4 * 4} \sum S_{i,j} = 1.6875$ 。

虽然我们这里没有考虑不同的stride的影响，不过原理是和之前的讨论相似的，读者不妨自行分析研究。

FesianXu

发布了111 篇原创文章 · 获赞 206 · 访问量 28万+

私信关注

Conv卷积层的反向求导细节

前言

卷积层的前向传播和反向传播

猜你喜欢