论相机中心投影中，相机中心的作用

论相机中心投影中，相机中心的作用

2019/12/3 FesianXu

前言

在中心投影中，相机中心作为聚集光线的理想中心，其具有核心的作用，本文参考[1]中的讨论，加上一些见解，作为笔者学习过程中的笔记。

如有谬误，请联系指正。转载请注明出处。

$\nabla$ 联系方式：
e-mail: [email protected]
QQ: 973926198
github: https://github.com/FesianXu

---

为了将三维空间中的点投射到二维空间，这也正是摄像机做的事情，我们引入了投影矩阵 $P_{3 \times 4}$，在齐次坐标系下，我们有：
$\left(\begin{matrix}x \\y \\w\end{matrix}\right) = P_{3 \times 4} \left(\begin{matrix}X \\Y \\Z \\T\end{matrix}\right)\tag{1.1}$
如果考虑到三维空间中的像点在同一个平面上，比如最简单的，考虑平面 $Z = 0$，我们便有：
$\left(\begin{matrix}x \\y \\w\end{matrix}\right) = H_{3 \times 3} \left(\begin{matrix}X \\Y \\T\end{matrix}\right)\tag{1.2}$
我们把公式(1.2)称之为投影变换（projective transformation）。

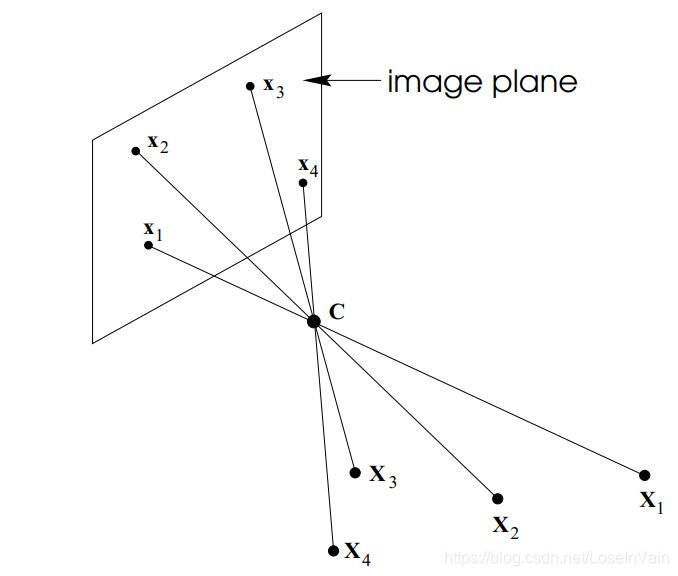
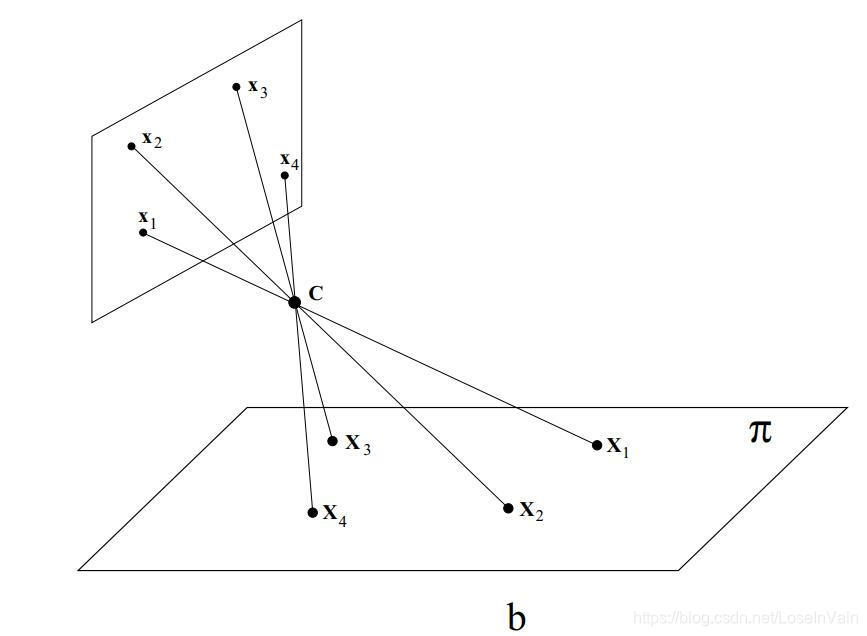
如图Fig 1所示，所有的像点 $X_i$都通过了焦点也就是相机中心。这种情况下，我们一般就用公式(1.1)进行描述，当像点都位于同一平面 $\pi$时，如Fig 2所示，我们用公式(1.2)进行描述，此时的 $H_{3 \times 3}$我们称之为单应性矩阵，其变换保留了共线性，见[2]的讨论。

Fig 1. 中心投影，将三维像点投影到二维平面上，通过了焦点C。

Fig 2. 当像点都位于同一平面时，我们把它看成是单应性变换，其保留了共线性。

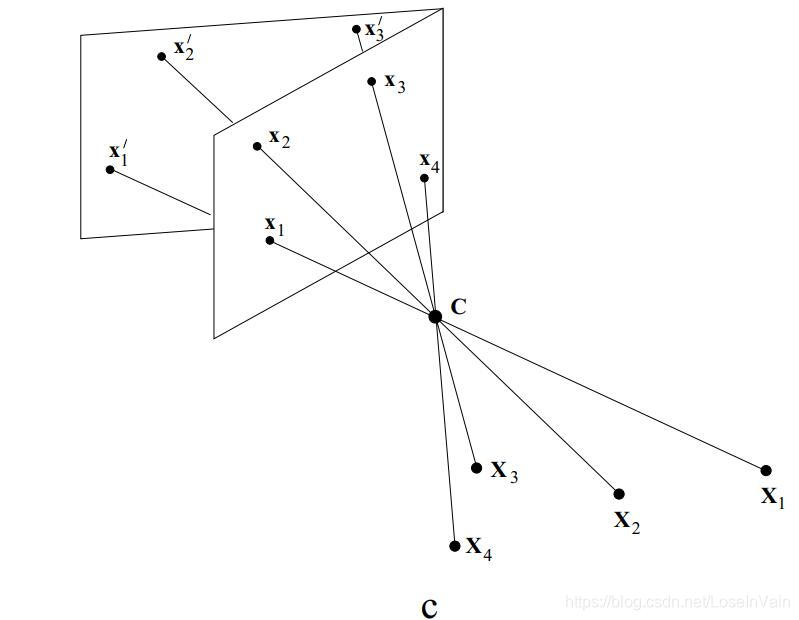
更特殊的是，共用同一个焦点的图像，可以通过投影变换（也就是单应性变换）进行转换，见Fig 3所示，其转换公式如：
$\mathbf{x}_i^1 = H_{3 \times 3} \mathbf{x}_i^2\tag{1.3}$
公式(1.3)实现了在 $\pi_{2}$上的点 $\mathbf{x}_i^2$到面 $\pi_{1}$的点 $\mathbf{x}_i^1$的转换。

Fig 3. 当不同二维图像共用同一个焦点时，不同图像可以通过投影变换进行转换。

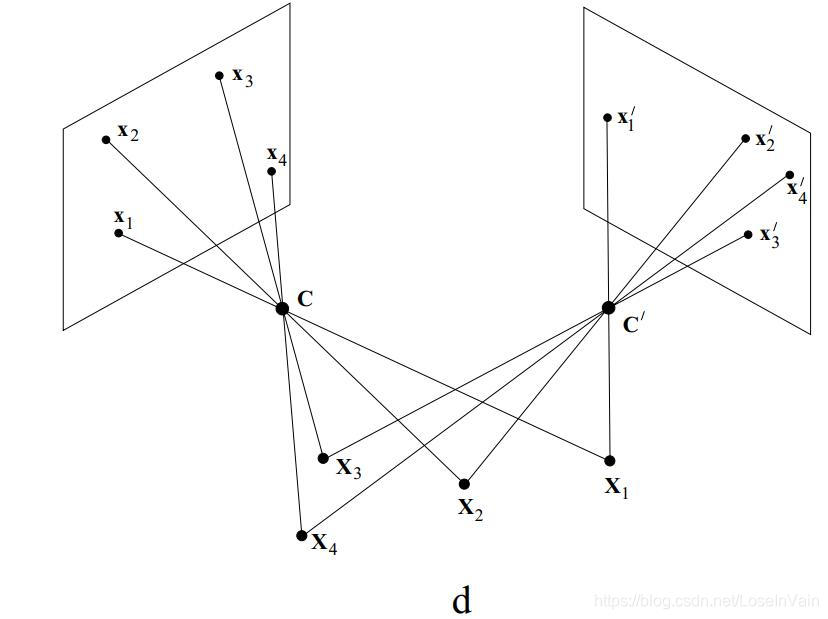
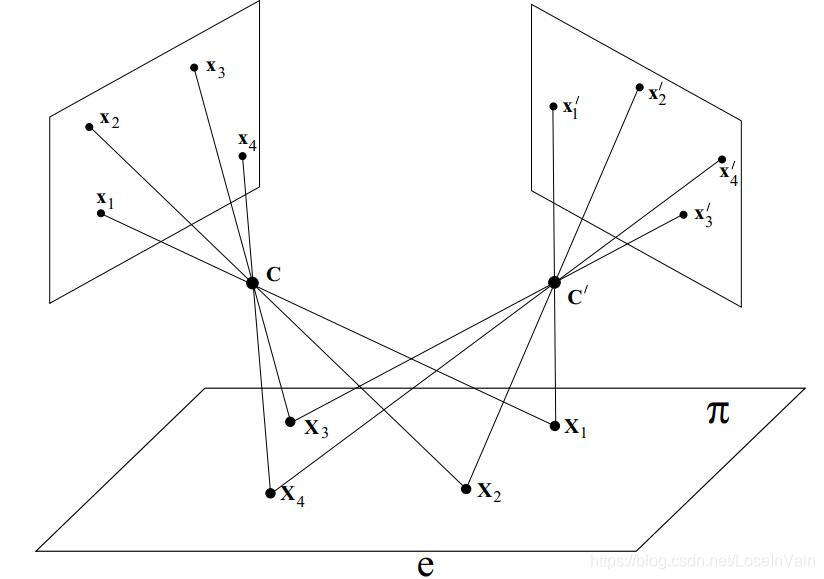
不过如果焦点移动了，那么一般来说就不能用投影变换进行不同面之间的转换了，如Fig 4所示，除非像点都在同一面上，那么仍然可以用投影变换进行不同面的点的转换，如Fig 5所示，这个可以见[2]的讨论。

扫描二维码关注公众号，回复： 8625999 查看本文章

Fig 4. 当焦点移动后，如果像点不在同一个面上，那么不同面的点不能用投影变换进行转换。

Fig 5. 但是如果像点都在同一个面上，那么不同面的点仍然满足共线性，可以用投影变换进行描述。

---

Reference

[1]. Hartley R, Zisserman A. Multiple view geometry in computer vision[M]. Cambridge university press, 2003. Page 8 Fig 1.1 The camera centre is the essence.

[2]. https://blog.csdn.net/LoseInVain/article/details/102739778