MVG学习笔记(2) --相机投影

版权声明：本文为博主原创文章，未经博主允许不得转载。 https://blog.csdn.net/YuYunTan/article/details/83384678

相机投影

  本博文议题是图像形成过程，即三维世界的二维表示的形成，以及我们可以从中推断出图像中出现的3D结构。

  从三维世界到二维图像的下降是我们失去一个维度的投影过程。 建模此过程的常用方法是通过中心投影(central projection)，其中来自空间点的光线从3D世界点通过空间中的固定点（投影中心）绘制。 该光线将与选择作为图像平面的空间中的特定平面相交。 光线与图像平面的交点表示该点的图像。 如果3D结构位于平面上，则尺寸不会下降。

  该模型与相机的简单模型一致，其中来自世界各点的光线穿过相机的镜头并照射在胶片或数字设备上，产生该点的图像。 忽略焦点和镜头厚度等影响，合理的近似是所有光线都通过一个点，即镜头的中心。

  在将投影几何应用于成像过程时，习惯上将世界建模为3D投影空间，等于 $\rm IR^3$和无穷远处的点。

  类似地，图像的模型是2D投影平面 $\rm IP^2$。中心投影只是从 $\rm IP^3$到 $\rm IP^2$的映射。如果我们考虑用齐次坐标 $(\rm X,Y,Z,T)^T$写的 $\rm IP^3$中的点，并让投影的中心是原点 $(0,0,0,1)^T$，那么我们看到的是固定的X，Y和Z的所有点 $(\rm X,Y,Z,T)^T$，但是变化的T形成穿过投影的点中心的单个光线，因此全部映射到相同的点。因此， $(\rm X,Y,Z,T)$的最后一维坐标与点成像的位置无关。实际上，图像点是 $\rm IP^2$中具有齐次坐标 $(\rm X,Y,Z)^T$的点。因此，映射可以由3D齐次坐标的映射表示，由3×4矩阵P表示，块结构 $\rm P=[I_{3\times3}| 0_3]$，其中 $\rm I_{3\times 3}$是3×3单位矩阵和 $0_3$是3维的零矢量。

  考虑到不同的投影中心和图像中的不同投影坐标系，可以看出最一般的成像投影由秩为3的任意 $3×4$矩阵表示，用于将在 $\rm IP^3$的点的齐次坐标映射成 $\rm IP^2$中的成像点。该矩阵P被称为相机矩阵。

  总之，投影相机对空间中的点的动作可以用齐次坐标的线性映射表示

$\left( \begin{matrix} x \\ y \\ w \end{matrix} \right) =\rm P_{3\times 4} \left( \begin{matrix}\rm X \\ Y \\ Z \\ T \end{matrix}\right)$

  此外，如果所有点都位于一个平面上（我们可以选择它作为平面 $\rm Z = 0$)，那么线性映射会减少到

$\left( \begin{matrix} x \\ y \\ w \end{matrix} \right) = \rm H_{3\times 3} \left( \begin{matrix}\rm X \\ Y \\ T \end{matrix}\right)$

  这是一种射影变换。

相机作为点

  在中心投影中， $\rm IP^3$中的点被映射到 $\rm IP^2$中的点，光线中的所有点穿过投影中心投射到图像中的相同点。

  出于图像投影的目的，可以将沿着这种光线的所有点视为相等。

  我们可以更进一步，并想象通过射影中心的光线代表图像点。因此，所有图像点的集合与通过相机中心的光线集相同。
  如果我们通过它的前三个坐标 $(\rm X,Y,Z)^T$表示从 $(0,0,0,1)^T$到点 $(\rm X,Y,Z,T)^T$的光线，很容易对于任何常数 $k$，光线 $k(\rm X,Y,Z)^T$表示相同的光线。因此，光线本身由齐次坐标表示。

  事实上，它们构成了二维光线空间。该组光线本身可以被认为是图像空间 $\rm IP^2$的表示。

  在图像的这种表示中，所有重要的是相机中心，因为单独确定形成图像的光线组。

  表示来自相同射影中心的图像形成的不同相机矩阵仅反映形成图像的一组光线的不同坐标系。

  因此，从空间中的相同点拍摄的两个图像是射影(projectively)等效的。

  只有当我们开始测量图像中的点时，才需要指定图像的特定坐标系。只有这样才有必要指定特定的相机矩阵。简而言之，我们现在忽略的模视场（modulo field-of view），假定使用相同摄像机中心采集的所有图像都是等效的 - 它们可以通过射影变换相互映射，而无需任何关于3D点或摄像机中心位置的信息。这些问题如图1所示。

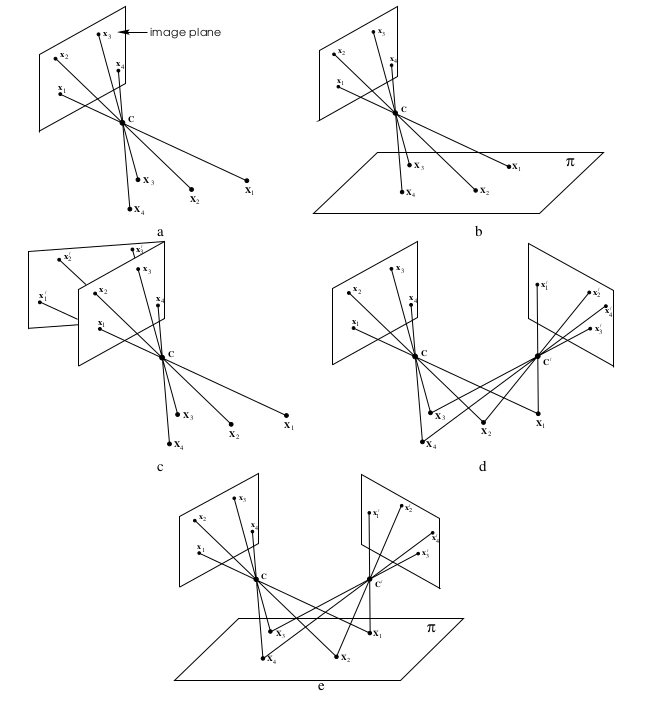
图1 相机中心是必不可少的。 （a）图像形成：图像点 $X_i$是平面与来自空间点 $X_i$的光线通过相机中心C的交点。（b）如果空间点是共面的，则在世界和图像之间存在射影变换， ${\mathbf {\rm x}_i} ={\rm H}_{3\times3}{\rm X}_i$ 。 （c）具有相同摄像机中心的所有图像通过射影变换相关， ${\mathbf {\rm x'}_i} ={\rm H'}_{3\times3}{\rm X}_i$。 比较（b）和（c） - 在两种情况下，都是通过中心的光线从一个平面映射到另一个平面。 在（b）中，映射在场景和图像平面之间，在（c）两个图像平面之间。 （d）如果摄像机中心移动，那么图像通常与射影变换无关，除非（e）所有空间点都是共面的。

校准相机

  为了充分理解图像与世界之间的欧几里德关系，有必要表达它们的相对欧几里德几何。

  正如我们所看到的，3D世界的欧几里德几何是通过将 $\mathcal{\rm IP}^2$中的特定平面指定为无穷远处的平面,以及该平面中的特定二次曲线 $\Omega$确定为绝对二次曲线来确定的。

  对于不在无穷远平面上的摄像机，世界上无穷远的平面一对一地映射到图像平面上。

  这是因为图像中的任何点都定义了空间中的光线，该光线在单个点中与无穷远的平面相交。

  因此，世界上无穷远的平面并没有告诉我们关于图像的任何新内容。

  绝对二次曲线，无论是无穷远平面上的二次曲线，都必须投影到图像中的二次曲线。 得到的图像曲线称为绝对二次曲线的图像，或称为IAC 。 如果图像中已知IAC的位置，则我们说相机已校准。

  在校准的相机中，可以确定从图像中的两个点反投影的两条光线之间的角度。我们已经看到，空间中两条线之间的角度取决于它们相对于绝对二次曲线在无穷远处与平面相交的位置。

  在校准的相机中，无穷远处的平面和绝对二次曲线 $\Omega_\infty$一对一地投影到图像平面和IAC上，表示为 $\omega$。两个图像点和 $\omega$之间的投影关系恰好等于背投影光线与无穷远平面的交点之间的关系，以及 $\Omega_\infty$。因此，知道IAC，可以通过图像中的直接测量来测量光线之间的角度。因此，对于校准的相机，可以测量光线之间的角度，计算由图像块表示的视场或确定图像中的椭圆是否向后投射到二次曲线。稍后，我们将看到它有助于我们确定重建场景的欧几里德结构。

绘画的3D重建

  使用射影几何技术，在许多情况下可以从单个图像重建场景。 如果不对成像场景做出一些假设，就无法做到这一点。

通过单幅图片重建一般是基于对场景结构的一些分析

   典型的技术涉及分析诸如平行线和消失点(vanishing points,也叫灭点)之类的特征以确定场景的仿射结构，例如通过确定图像中观察到的平面的无穷远线。 关于在场景中观察到的角度的知识（或假设），尤其是正交线或平面，可以用于将仿射重建升级为欧几里德。

  这种技术尚不可能是全自动的。 然而，射影几何知识可以构建到允许由用户引导的场景的单视图重建的系统中。

  这些技术已被用于重建从旧主绘画衍生的3D纹理映射图形模型。 从文艺复兴时期开始，制作了具有极其准确视角的绘画。 在下图中，示出了从这样的绘画进行的重建。

图2。 单视图重建。 （a）原画 - 圣杰罗姆在他的研究中，1630年，Hendrick van Steenwijck（1580-1649），Joseph R. Ritman私人收藏，荷兰阿姆斯特丹。 （b）（c）（d）从绘画中创建的3D模型的视图。 数字由Antonio Criminisi提供。