李宏毅深度学习笔记（六）逻辑回归

设置函数

我们可以找到一个函数 $P_{w,b}(C_1|x)$，如果 $P_{w,b}(C_1|x)\ge0.5$则输出 $C_1$，否则输出 $C_2$。
逻辑回归的模型如下：
$P_{w,b}(C_1|x)=\sigma(z)$

$z=wx+b=\sum_{i=1}^nw_ix_i+b$

$\sigma(z)=\frac{1}{1+exp(-z)}$

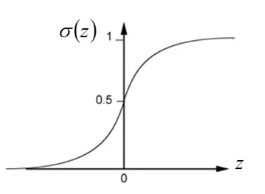
所以我们设置函数为：

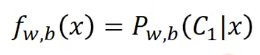
判断函数的好坏

假设我们有下面的一组数据：

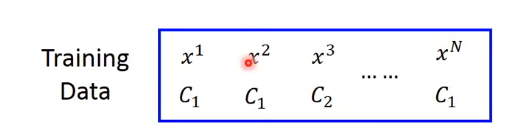
我们假定数据是依据函数 $f_{w,b}(x)=P_{w,b}(C_1|x)$生成的，那么接下来我们就要求取参数 $w$和 $b$了。
我们定义：

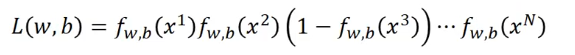
最有可能让训练集呈现上面的样子的是使 $L(w,b)$最大的 $w^*$和 $b^*$，即：

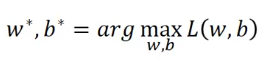
为了简化计算，我们对上式进行一下转换：

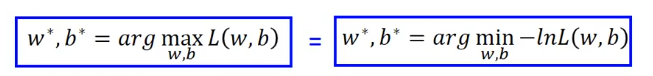
这时候原本的乘法就变成了加法：

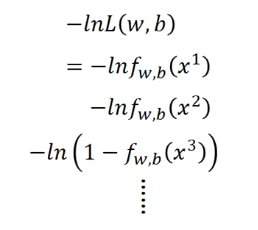
又（这里用到了交叉熵.），我们定义 $-lnL(w,b)$为交叉熵损失函数

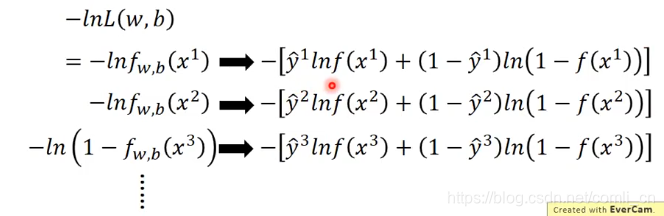
找一个最好的函数

交叉熵损失函数对 $w_i$求偏导（这里用到了求导的链式法则）

进行化简得：

逻辑回归和线性回归的对比

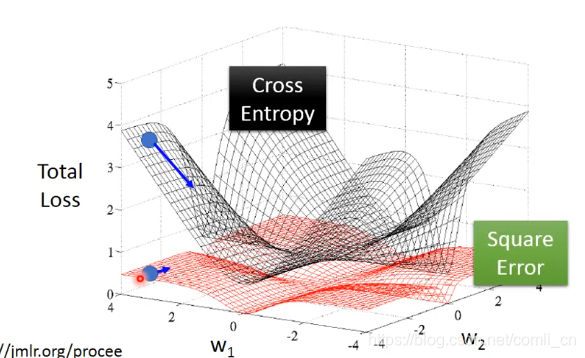
为什么逻辑回归不用平方损失函数

如果我们在逻辑回归中用了平方损失函数的话：

我们可以看到，如果目标值 $\hat y^n=1$，当 $f_{w,b}(x^n)=1$时，偏导数为0，也就是说因为我们计算出来的值跟目标值是一样的所以不需要更新，这是正确的。但当 $f_{w,b}(x^n)=0$的时候，平方损失函数的偏导数为0，也就是说不需要更新，但事实上我们的计算值离实际值很远。
同样的情况会出现在 $\hat y^n=0$中。