必备知识:
高斯消元,图论基本知识(好像就这。。。(雾))
这里是无向图部分,请不要走错场。。。
定义
我们将邻接矩阵定义为矩阵\(A(u,v)\),我想邻接矩阵就不用再多说了;
我们将每个点的度数矩阵定义为矩阵\(D(u,v)\),这里再加上数学表示;
\(D(u,u)=u\)这个点的度数,\(D(u,v)=0(u!=v)\);
我们将矩阵Laplace(或Kirchhoff)定义为\(L(u,v)=D(u,v)-A(u,v)\)
我们将生成树的个数定义为 \(t\);
引入
这里将讲述行列式,如果dalao已经学过,请直接跳过这个环节;
这里引入的是\(N*N\)方阵行列式(因为邻接矩阵是方形),例如
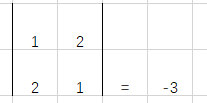
行列式的公式是
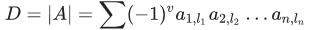
PS:其中v是 \(l_1 , l_2 , l_3 ... l_n\)的逆序对个数;
行列式有几个性质:
- 行行交换,结果相反;
- 行行叠加,结果不变;
- 矩阵行伸长,结果等比例增加;
PS:
性质1的简单证明:
由行列式的公式可知,行行交换,必然会出现逆序对的变化,变化为1,那么此时结果符号一定会改变;
性质2的补充:
可以让其他行乘上k叠加到这一行,结果不变;
根据这些,我们就可以发现,高斯消元可以很好的利用这些性质,那么高斯消元后矩阵对角线的乘积即为结果;
我从其他位置挖来了一个矩阵L的优化证明,说实话,我有点蒙

我们根据这个性质可以少算一行一列,这应该也算优化吧(心虚~
应用
这样思路就十分清晰了,这里的矩阵L行列式值即为生成树个数,那么我们就有了步骤:
- 首先构造矩阵L,根据公式\(L=D - A\),我们可以很方便地求出矩阵L,当然,在读入边时就可以直接操作,如边 \(u\) -> \(v\),我们不妨让\(f [ u ] [ v ]=f [ v ] [ u ] - -,f [ u ] [ u ]++,f [ v ] [ v ]++\).
- 然后将矩阵高斯消元,并求出对角线的乘积。
- 有时因为必须是整数,我们可以采用类似于辗转相除法的减去方法,下面将详细介绍。
模型
模板题:小Z的房间
思路清晰,只要将一个点和上下左右建边,构造矩阵L,用高斯消元求解;
不过高斯消元一般求其小数形式,这里是不行的,因为是方案数(不可能是小数啊QWQ);
这里就应用了类似于辗转相除的方法,回顾辗转相除,将两个数取\(mod\),然后交换位置,直到一个为0为止;
高斯消元同样是将另一个数消为0,那么我们将函数改一下,如下(看注释):
ll Gauss(){
ll ans=1;n=cent-1;//定理 1 的应用 ,cent为总点数
for(int i=1;i<=n;i++){
for(int j=i+1;j<=n;j++){
while(f[j][i]){//类辗转相除法 ,直到一个为0
int t=f[i][i]/f[j][i];
//注意是int类型(向下取整),没减完,但是减后f[i][i]<f[j][i]
for(int k=i;k<=n;k++)
f[i][k]=(f[i][k]-f[j][k]*t%mod+mod)%mod;
swap(f[i],f[j]);//交换位置辗转减
//交换位置是因为上面所说的 f[i][i]<f[j][i]
ans=-ans;//交换位置要取反
}
}
ans=(ans*f[i][i]+mod)%mod;
}
return ans;
}应该解释的还算清楚,类似辗转相除的复杂度大约多了一个\(log n\),总复杂度\(O(n^{3}log n)\)我将整个代码放在这里,算一个模板吧:
#include<bits/stdc++.h>
#define ll long long
#define mod 1000000000
using namespace std;
int n,m,a[100][100],cent;
ll f[100][100];
inline void add(int u,int v){
f[u][u]++,f[u][v]--;
}//由于矩阵对称,所以加减一次就好。。。
ll Gauss(){
ll ans=1;n=cent-1;//定理 1 的应用 ,cent为总点数
for(int i=1;i<=n;i++){
for(int j=i+1;j<=n;j++){
while(f[j][i]){//类辗转相除法 ,直到一个为0
int t=f[i][i]/f[j][i];
//注意是int类型(向下取整),没减完,但是减后f[i][i]<f[j][i]
for(int k=i;k<=n;k++)
f[i][k]=(f[i][k]-f[j][k]*t%mod+mod)%mod;
swap(f[i],f[j]);//交换位置辗转减
//交换位置是因为上面所说的 f[i][i]<f[j][i]
ans=-ans;//交换位置要取反
}
}
ans=(ans*f[i][i]+mod)%mod;
}
return ans;
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++){
char s=getchar();
while(s!='.'&&s!='*')
s=getchar();//防止输入出错
if(s=='.') a[i][j]=++cent;//命名
}
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++){
int now,rou;
if(!(now=a[i][j])) continue;
if(rou=a[i-1][j]) add(now,rou);
if(rou=a[i][j-1]) add(now,rou);
if(rou=a[i+1][j]) add(now,rou);
if(rou=a[i][j+1]) add(now,rou);//构建L矩阵
}
printf("%lld\n",(Gauss()+mod)%mod);//不能是负数。。。
}深入
懂了模板当然是不够的,我们应该见识一些技巧:
[SDOI2014]重建
题目不再粘贴,我们直接叙述;
这里同样是生成树个数,不过不同的是,这里具有边权值,不过这里并不碍事,我们将叙述有点权值将如何应对。
根据高中概率的基本知识,两个没有交集的事件\(A,B\),概率分别为\(P(A),P(B)\),那么\(P(AB)=P(A)*P(B)\),这个应该都懂。
那么每条边联通的概率为\(P(u,v)\),那么不连通的概率是\(1-P(u,v)\),这个应该很显然。
那么一个生成树的概率\(P(G)= P(u,v)*(1 - P(x,y))\),其中u,v的边属于生成树\(G\),而\(x,y\)这条边不属于。
那么,\(\sum P(G)\)即为总概率,我们将式子改造。
\[\sum_{G} \prod_{(u,v)\in G,(x,y)\notin G} P(u,v)*(1-P(x,y))=\sum_G \prod_{(u,v)\in G,(x,y)\notin G} P(u,v)*(1-\frac{P(G)}{P(u,v)})=\sum_G (1 - P(G))\prod_{(u,v)\in G,(x,y)\notin G} \frac{P(u,v)}{1-P(u,v)}\]
解释一下,由于属于树\(G\)的边和不属于树\(G\)的边互为补集,所以就可以利用这个性质,我直接表达这个式子
\(sum=\sum(1-P(G)) \prod_{(u,v)\in G,(x,y)\notin G} \frac{P(u,v)}{1-P(u,v)}\)
这样就很显然了,将\(\frac{P[u][v]}{1-P[u][v]}\)作为边权值,不过如何处理边权,这里给出步骤:
1.我们将矩阵读入,重新定义边权;
2.将边权当作度数加在对角线上,然后当作邻接矩阵中边的个数减去即可;
3.高斯消元;
介绍完毕,Code:
#include<bits/stdc++.h>
#define maxn 57
#define db double
using namespace std;
int n;
db f[maxn][maxn],ans=1.0;
const db eps=1e-8;
db Gauss(){
n--;db ol=1.0;
for(int i=1;i<=n;i++){
int sp=i;
for(int j=i+1;j<=n;j++)
if(fabs(f[j][i])>fabs(f[sp][i])) sp=j;
if(i!=sp) swap(f[i],f[sp]),ans=-ans;
for(int j=i+1;j<=n;j++){
db t=f[j][i]/f[i][i];
for(int k=i;k<=n;k++)
f[j][k]-=f[i][k]*t;
}
ol*=f[i][i];
}
return ol;
}//这里是小数,所以操作就没有那么鬼畜了。。
//sum = sigma P(G) Π(P[u][v]/(1-P[u][v]));
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
scanf("%lf",&f[i][j]);
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
db t=max((1.0-f[i][j]),eps);//小心 0 哦
if(i>j) ans*=t;//累加,得出 1-P(G)
f[i][j]/=t;//步骤1
}
}
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
if(i!=j){
f[i][i]+=f[i][j];
f[i][j]=-f[i][j];
}//步骤2 ,构图
printf("%.10lf",fabs(Gauss()*ans));
}[SHOI2016]黑暗前的幻想乡
这里用到了容斥原理,二进制枚举等技巧,容斥我就不再叙述,自己不会可以yy一下(逃~
直接上代码了(有良心注释)
#include<bits/stdc++.h>
#define maxn 19
#define ll long long
#define mod 1000000007
using namespace std;
int n,m;
vector<pair<int ,int > >a[maxn];
ll f[maxn][maxn],ans;
ll Gauss(){
int m=n-1;ll ol=1;
for(int i=1;i<=m;i++){
for(int j=i+1;j<=m;j++){
while(f[j][i]){
int t=f[i][i]/f[j][i];
for(int k=i;k<=m;k++)
f[i][k]=(f[i][k]-f[j][k]*t%mod+mod)%mod;
swap(f[i],f[j]);ol=-ol;
}
}
ol=ol*f[i][i]%mod;
}
return (ol+mod)%mod;
}//唉,方案数。。。
void add(int u,int v){
f[u][u]++,f[v][v]++;
f[u][v]--,f[v][u]--;
}
int main(){
scanf("%d",&n);
for(int i=1,t,u,v;i<=n-1;i++){
scanf("%d",&t);
while(t--){
scanf("%d%d",&u,&v);
a[i].push_back(make_pair(u,v));//存图
}
}
int lim=1<<(n-1);
for(int i=1;i<lim;i++){
int cnt=0;memset(f,0,sizeof(f));//暴力建图
for(int k=0;k<n-1;k++){//二进制枚举
if((1<<k)&i){
cnt++;
for(int j=0;j<a[k+1].size();j++)
add(a[k+1][j].first,a[k+1][j].second);
}
}
if((n-cnt)&1) ans=(ans+Gauss())%mod;
//容斥原理。。。其实就是奇数和偶数分别加减 。。。
else ans=(ans-Gauss()+mod)%mod;//防止负数。。。
}
printf("%lld\n",ans);
}总结
其实还有一些内容,但是由于赶着复习,就没再说了。
我们做的这几道题,无非是建图,统计答案,高斯消元时设下关卡,导致题目难度的跃升。
但既然已经知道要考哪里,就往哪个地方想,就像专题训练一样,然后找出特点,从而在综合题中找到这个算法的影子;
这个算法特点主要就是生成树的计数,所以应该很好看出来,记住特点和处理方法,培养数学思维才是做题目的;