BZOJ 1494: [NOI2007]生成树计数 矩阵树定理 || 状压DP+矩阵快速幂

其他 2019-04-30 09:01:00 阅读次数: 0
版权声明：https://blog.csdn.net/huashuimu2003 https://blog.csdn.net/huashuimu2003/article/details/89603854

title

BZOJ 1494
LUOGU 2109
Description

最近，小栋在无向连通图的生成树个数计算方面有了惊人的进展，他发现：
n n 个结点的环的生成树个数为 n n 。
n n 个结点的完全图的生成树个数为 n n − 2 n^{n-2} 。
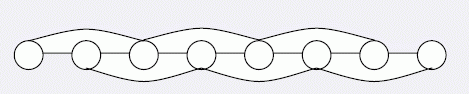
这两个发现让小栋欣喜若狂，由此更加坚定了他继续计算生成树个数的想法，他要计算出各种各样图的生成树数目。一天，小栋和同学聚会，大家围坐在一张大圆桌周围。小栋看了看，马上想到了生成树问题。如果把每个同学看成一个结点，邻座（结点间距离为1）的同学间连一条边，就变成了一个环。可是，小栋对环的计数已经十分娴熟且不再感兴趣。于是，小栋又把图变了一下：不仅把邻座的同学之间连一条边，还把相隔一个座位（结点间距离为2）的同学之间也连一条边，将结点间有边直接相连的这两种情况统称为有边相连，如图1所示。
在这里插入图片描述
小栋以前没有计算过这类图的生成树个数，但是，他想起了老师讲过的计算任意图的生成树个数的一种通用方法：构造一个 n × n n×n 的矩阵 A = { a i j } A=\left\{a_{ij}\right\} ,其中
在这里插入图片描述
其中di表示结点i的度数。与图1相应的A矩阵如下所示。为了计算图1所对应的生成数的个数，只要去掉矩阵A的最后一行和最后一列，得到一个 ( n − 1 ) × ( n − 1 ) (n-1)×(n-1) 的矩阵 B B ，计算出矩阵B的行列式的值便可得到图1的生成树的个数所以生成树的个数为 ∣ B ∣ = 3528 |B|=3528 。小栋发现利用通用方法，因计算过于复杂而很难算出来，而且用其他方法也难以找到更简便的公式进行计算。于是，他将图做了简化，从一个地方将圆桌断开，这样所有的同学形成了一条链，连接距离为1和距离为2的点。例如八个点的情形如下：
在这里插入图片描述
这样生成树的总数就减少了很多。小栋不停的思考，一直到聚会结束，终于找到了一种快捷的方法计算出这个图的生成树个数。可是，如果把距离为3的点也连起来，小栋就不知道如何快捷计算了。现在，请你帮助小栋计算这类图的生成树的数目。

Input

包含两个整数k,n，由一个空格分隔。k表示要将所有距离不超过k（含k）的结点连接起来，n表示有n个结点。

Output

输出一个整数，表示生成树的个数。由于答案可能比较大，所以你 只要输出答案除65521 的余数即可。

Sample Input

3 5

Sample Output

75

HINT

在这里插入图片描述
在这里插入图片描述

analysis

跟随着yyb大佬的步伐一起从头到尾写一遍。

  • T a s k 1   60 p t s ： k ≤ 5 , n ≤ 100 Task1 \text{ }60 pts：k≤5,n≤100
    送分的一档。
    直接暴力构图，矩阵树定理直接算就好了。
    时间复杂度 O ( n 3 ) O(n^3) 。
    但是我不会矩阵树定理（雾），所以特地去学了一下。其实还好啦。
    矩阵树定理
#include<bits/stdc++.h>
using namespace std;
const int mod=65521;
const int maxn=111;

template<typename T>inline void read(T &x)
{
	x=0;
	T f=1, ch=getchar();
	while (!isdigit(ch) && ch^'-') ch=getchar();
	if (ch=='-') f=-1, ch=getchar();
	while (isdigit(ch)) x=(x<<1)+(x<<3)+(ch^48), ch=getchar();
	x*=f;
}
int f[maxn][maxn],ans=1;
int main()
{
	int k,n;
	read(k);read(n);
	for (int i=1; i<=n; ++i)
		for (int j=i+1; j<=min(n,i+k); ++j)
			++f[i][i],++f[j][j],--f[i][j],--f[j][i];
	for (int i=2; i<=n; ++i)
		for (int j=i+1; j<=n; ++j)
			while (f[j][i])
			{
				int t=f[i][i]/f[j][i];
				for (int k=i; k<=n; ++k)
					f[i][k]=(f[i][k]-1ll*f[j][k]*t%mod)%mod,swap(f[i][k],f[j][k]);
				ans=-ans;
			}
	for (int i=2; i<=n; ++i)
		ans=(1ll*ans*f[i][i])%mod;
	printf("%d\n",ans);
	return 0;
}

  • T a s k 2   80 p t s ： k ≤ 5 , n ≤ 10000 Task2 \text{ }80pts：k≤5,n≤10000
    这档分其实写出来基本就会满分了
    发现 k k 的范围十分的小，也就是每个点的边并不会很多
    换而言之，如果一个点要和前面的所有点处在一个生成树中
    意味着它必须和前面k个点中的至少一个处在同一个联通块中
    所以，我们只需要考虑当前点和它前面 K K 个点的状态就行了

  • 那么，我们的状态是什么？
    我们思考一下，对于生成树而言，我们比较在意的只有两个方面：联通块和边
    对于相邻的 K K 个点，单独拿出来显然是一个完全图，因此不需要考虑边的问题
    所以，我们的状态和联通块有关。
    现在的问题又变成了如何记录前面 k k 个点的联通块呢？
    我们可以按照顺序编号，保证任意一个编号的联通块在出现之前，所有小于它的编号都已经出现过。（最小表示法吼啊）
    （不一定要这样，只需要一种能够保证所有相同的联通块方案只会被算一次就行了）
    编完号之后，我们可以把前面 k k 个点所在的联通块给压成十进制
    因为 k ≤ 5 k≤5 ，就只需要三个二进制位，所以可以用八进制来把联通块的情况给压成十进制位。
    那么，不同的联通块方案数有多少呢？
    相当于把 n n 个球放进任意数量个集合，也就是 B e l l Bell 数，算出来是 52 52 种

  • 我们不关心每个联通块之间的连接方案，我们只关心如何对于两种联通块之间进行转移
    所以我们可以枚举当前点和前面 k k 个点的连边方案（最多就 k k 条边）
    然后暴力（用并查集）判断是否成环，
    同时，最前面的那个点也必须和当前这 k k 个点中的一个在同一个联通块中
    这样就可以转移到另外一个联通块的情况
    再用上面的最小表示法把它的编号还原出来
    这样证明可以从当前状态向后面的状态进行转移。

  • d p dp 要的是初始状态和转移。
    显然搞出来了转移，考虑初始状态。
    显然不能一开始不满 k k 个点
    所以直接从 k k 个点开始计算
    因为每个联通块之间是完全图，所以可以暴力计算联通块大小为 x x 时的方案数
    那么 k k 个点时，某个联通块情况的方案数就是 ∏ n u m s i z e ∏num_{size}
    联通块大小为1,2时，有1种方法
    联通块大小为3有3种
    联通块大小为4有16种
    联通块大小为5有125种。

  • 这样子，我们就可以 O ( 52 ∗ 2 5 ∗ K 2 + n ∗ 5 2 2 ) O(52∗2^5∗K^2+n∗52^2) 转移了
    这样子可以过 80 p t s 80pts 

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int mod=65521;
const int maxn=55;

template<typename T>inline void read(T &x)
{
	x=0;
	T f=1, ch=getchar();
	while (!isdigit(ch) && ch^'-') ch=getchar();
	if (ch=='-') f=-1, ch=getchar();
	while (isdigit(ch)) x=(x<<1)+(x<<3)+(ch^48), ch=getchar();
	x*=f;
}

ll n;
int k,cnt;
int p[1<<20],st[maxn];
inline bool check(int t)//检查一个状态是否合法
{
	int tmp=1<<1;//因为第一个点一定属于一号联通快，所以先把一号联通快放进去检查
	for (int i=3; i<k*3; i+=3)
	{
		for (int j=1; j<( (t>>i)&7 ); ++j)
			if (!( tmp& (1<<j) )) return false;//检查比当前编号小的所有编号是否都已经出现过
		tmp|=1<<( (t>>i)&7 );//将当前编号也给放进来
	}
	return true;
}

inline void dfs(int x,int t)//暴力找出所有状态，每个编号利用3个二进制位存
{
	if (x==k)
	{
		if (check(t)) p[t]=++cnt,st[cnt]=t;
		return ;
	}
	for (int i=1; i<=k; ++i)
		dfs(x+1,t|( i<<(x*3) ));
}

int fa[maxn],a[maxn];
inline int get(int x)
{
	return x==fa[x]?x:fa[x]=get(fa[x]);
}

int f[11111][maxn],g[maxn][maxn];
int main()
{
	read(k);read(n);
	dfs(1,1);
	for (int i=1; i<=cnt; ++i)
	{
		f[k][i]=1;
		memset(a,0,sizeof(a));
		for (int j=0; j<k; ++j) ++a[ ( st[i]>> (j*3) )&7 ];
		for (int j=1; j<=k; ++j)
			if (a[j]==3) f[k][i]=3;
			else if (a[j]==4) f[k][i]=16;
			else if (a[j]==5) f[k][i]=125;

		int t=st[i];
		for (int s=0; s<=(1<<k)-1; ++s)//暴力枚举当前点对于前面几个点的连边状态
		{
			for (int j=0; j<=k; ++j) fa[j]=j;
			for (int j=0; j<k; ++j)//利用并查集维护联通性
				for (int l=j+1; l<k; ++l)
					if ( ( ( t>> (j*3) )&7 )==( ( t>> (l*3) )&7 ) )
						fa[get(j)]=get(l);

			bool cir=false;
			for (int j=0; j<k; ++j)//检查当前点的连边
				if (s&(1<<j))
				{
					if (get(k)==get(j))//出现了环
					{
						cir=true;
						break;
					}
					fa[get(k)]=get(j);
				}
			if (cir) continue;//连边不合法
			for (int j=1; j<=k; ++j)//最前面的点必须和后面的一个点联通，否则就无法联通了
				if (get(0)==get(j))
				{
					cir=true;
					break;
				}
			if (!cir) continue;

			int now=0,used=0;
			for (int j=0; j<k; ++j)//当前存在合法的联通方案，因此当前的状态可以转移到另外的一个状态上去
				if (!( now&( 7<< (j*3) ) ))//当前点不在任意一个联通块中
				{
					now|=++used<<(j*3);//新的联通块
					for (int l=j+1; l<k; ++l)//把所有在一个联通块里的点丢到状态里去
						if (get(j+1)==get(l+1))
							now|=used<<(l*3);
				}
			++g[i][p[now]];
		}
	}
	for (int i=k+1; i<=n; ++i)
		for (int j=1; j<=cnt; ++j)
			for (int l=1; l<=cnt; ++l)
				if (g[j][l])
					f[i][l]=(f[i][l]+1ll*g[j][l]*f[i-1][j])%mod;
	printf("%d\n",f[n][1]);
	return 0;
}
  • A C ： n ≤ 1 0 15 AC：n≤10^{15}
    明摆着 l o g log 算法，
    发现每次转移相同，直接矩阵快速幂就行了
    时间复杂度 O ( l o g n ⋅ 5 2 3 ) O(logn⋅52^3) ，预处理的时间写在上面了。。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int mod=65521;
const int maxn=55;

template<typename T>inline void read(T &x)
{
	x=0;
	T f=1, ch=getchar();
	while (!isdigit(ch) && ch^'-') ch=getchar();
	if (ch=='-') f=-1, ch=getchar();
	while (isdigit(ch)) x=(x<<1)+(x<<3)+(ch^48), ch=getchar();
	x*=f;
}

ll n;
int k,cnt;
int p[1<<20],st[maxn];
struct matrix
{
	int s[maxn][maxn];
	inline void Clear()
	{
		memset(s,0,sizeof(s));
	}
	inline void pre()
	{
		memset(s,0,sizeof(s));
		for (int i=1; i<=cnt; ++i)
			s[i][i]=1;
	}
}G;

inline matrix operator * (matrix a,matrix b)
{
	matrix res;res.Clear();
	for (int i=1; i<=cnt; ++i)
		for (int j=1; j<=cnt; ++j)
			for (int l=1; l<=cnt; ++l)
				res.s[i][j]=(res.s[i][j]+1ll*a.s[i][l]*b.s[l][j])%mod;
	return res;
}

inline matrix Quick_power(matrix a,ll b)
{
	matrix ans;ans.pre();
	while (b)
	{
		if (b&1)
			ans=ans*a;
		a=a*a;
		b>>=1;
	}
	return ans;
}

inline bool check(int t)//检查一个状态是否合法
{
	int tmp=1<<1;//因为第一个点一定属于一号联通快，所以先把一号联通快放进去检查
	for (int i=3; i<k*3; i+=3)
	{
		for (int j=1; j<( (t>>i)&7 ); ++j)
			if (!( tmp& (1<<j) )) return false;//检查比当前编号小的所有编号是否都已经出现过
		tmp|=1<<( (t>>i)&7 );//将当前编号也给放进来
	}
	return true;
}

inline void dfs(int x,int t)//暴力找出所有状态，每个编号利用3个二进制位存
{
	if (x==k)
	{
		if (check(t)) p[t]=++cnt,st[cnt]=t;
		return ;
	}
	for (int i=1; i<=k; ++i)
		dfs(x+1,t|( i<<(x*3) ));
}

int fa[maxn],a[maxn];
inline int get(int x)
{
	return x==fa[x]?x:fa[x]=get(fa[x]);
}

int f[maxn],g[maxn][maxn];
int main()
{
	read(k);read(n);
	dfs(1,1);
	for (int i=1; i<=cnt; ++i)
	{
		f[i]=1;
		memset(a,0,sizeof(a));
		for (int j=0; j<k; ++j) ++a[ ( st[i]>> (j*3) )&7 ];
		for (int j=1; j<=k; ++j)
			if (a[j]==3) f[i]=3;
			else if (a[j]==4) f[i]=16;
			else if (a[j]==5) f[i]=125;

		int t=st[i];
		for (int s=0; s<=(1<<k)-1; ++s)//暴力枚举当前点对于前面几个点的连边状态
		{
			for (int j=0; j<=k; ++j) fa[j]=j;
			for (int j=0; j<k; ++j)//利用并查集维护联通性
				for (int l=j+1; l<k; ++l)
					if ( ( ( t>> (j*3) )&7 )==( ( t>> (l*3) )&7 ) )
						fa[get(j)]=get(l);

			bool cir=false;
			for (int j=0; j<k; ++j)//检查当前点的连边
				if (s&(1<<j))
				{
					if (get(k)==get(j))//出现了环
					{
						cir=true;
						break;
					}
					fa[get(k)]=get(j);
				}
			if (cir) continue;//连边不合法
			for (int j=1; j<=k; ++j)//最前面的点必须和后面的一个点联通，否则就无法联通了
				if (get(0)==get(j))
				{
					cir=true;
					break;
				}
			if (!cir) continue;

			int now=0,used=0;
			for (int j=0; j<k; ++j)//当前存在合法的联通方案，因此当前的状态可以转移到另外的一个状态上去
				if (!( now&( 7<< (j*3) ) ))//当前点不在任意一个联通块中
				{
					now|=++used<<(j*3);//新的联通块
					for (int l=j+1; l<k; ++l)//把所有在一个联通块里的点丢到状态里去
						if (get(j+1)==get(l+1))
							now|=used<<(l*3);
				}
			++g[i][p[now]];
		}
	}
	
	for (int i=1; i<=cnt; ++i)
		for (int j=1; j<=cnt; ++j)
			G.s[i][j]=g[i][j];
	G=Quick_power(G,n-k);

	int ans=0;
	for (int i=1; i<=cnt; ++i)
		ans=(ans+1ll*G.s[i][1]*f[i])%mod;
	printf("%d\n",ans);
	return 0;
}

猜你喜欢

转载自blog.csdn.net/huashuimu2003/article/details/89603854
今日推荐
基于大语言模型的开源知识库问答系统 MaxKB GitHub Star 数量突破 5,000 个！
美国拟限制 AI 大模型出口中国和俄罗斯
苹果将与 OpenAI 达成协议，将 ChatGPT 应用于 iPhone
openKylin 社区生态委员会第六次会议圆满召开
阿里云正式发布通义千问 2.5
Python 3.13 发布首个 Beta：实验性自由线程模式和 JIT、改进交互式解释器
Stack Overflow 拿我的代码去训练 AI 大模型，还封了我的账号
Pop!_OS 的 COSMIC 桌面完成 App Store 上架工作
《2024 年一季度互联网投融资运行情况》研究报告
报告：Django 仍然是 74% 开发者的首选
15 年前上了“FFmpeg 耻辱柱”，今天他还得谢谢咱——腾讯QQPlayer一雪前耻？
TIOBE 5 月榜单：Fortran “复活”进入 Top 10
周排行
记一下去大梅沙的准备（2018-05-26）
Spring 注解 事务
基于HTTP协议的客户端缓存
阿里云rds 备份和还原
[PHP] 几个拖慢 PHP 程序/API 运行速度的点
python 代码风格------------PEP8规则
js控制json生成菜单——自制菜单（一）
将字符串: 'k:1|k1:2|k2:3|k3:4 ' ,处理成 python 字典: {'k':1, 'k1':2, ...}
微信小程序转支付宝小程序
Qt551.窗口滚动条
每日归档
更多
2024-05-13(18)
2024-05-12(0)
2024-05-11(38)
2024-05-10(38)
2024-05-09(35)
2024-05-08(42)
2024-05-07(14)
2024-05-06(40)
2024-05-05(0)
2024-05-04(7)

代码天地 © 2018 codetd.com

境外服务器   最新电视剧2022