支持向量机
一些基本的知识可以在 第二章感知机 中了解。在感知机中可以得到,对于线性可分数据集,感知机学习算法原始形式迭代是收敛的,但是存在很多解,为了得到唯一的超平面,需要增加约束条件,也就是支持向量机。
支持向量机学习的基本想法是求解能够正确划分训练数据集并且几何间隔最大的分离超平面。
间隔最大化
最大间隔分离超平面可以表示为下面的约束最优化问题:

约束条件表示的是超平面(w,b)关于每个训练样本点的几何间隔至少是γ。
考虑几何间隔和函数间隔的关系,可将这个问题改写为

这是一个等价的最优化问题。这样,就可以取  =1。将
=1。将  =1代入上面的最优化问题,注意到最大化
=1代入上面的最优化问题,注意到最大化![]() 和最小化
和最小化![]() 是等价的,于是就得到下面的线性可分支持向量机学习的最优化问题
是等价的,于是就得到下面的线性可分支持向量机学习的最优化问题
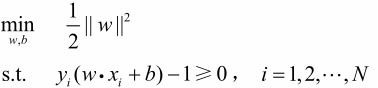
这是一个凸二次规划(convex quadratic programming)问题。
凸优化问题是指约束最优化问题
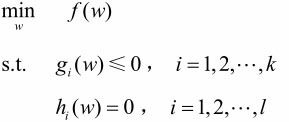
目标函数f(w)和约束函数gi(w)都是Rn上的连续可微的凸函数,约束函数hi(w)是Rn上的仿射函数。当目标函数f(w)是二次函数且约束函数gi(w)是仿射函数时,上述凸最优化问题成为凸二次规划问题。
如果求出约束最优化问题的解w*,b*,那么就可以得到最大间隔分离超平面w*·x + b*=0及分类决策函数f(x)=sign(w*·x + b*),即线性可分支持向量机模型。
线性可分训练数据集的最大间隔分离超平面是存在且唯一的。
假设存在两个最优解,(w1*,b1*) 和 (w2*,b2*) ,由于w >0,因此必有 ![]() ,又因为最优解时,
,又因为最优解时,![]() 等号成立,w*相等,那么b*必然也相等。
等号成立,w*相等,那么b*必然也相等。
支持向量和间隔边界
支持向量是使约束条件式 ![]() 等号成立的点,即
等号成立的点,即 ![]()
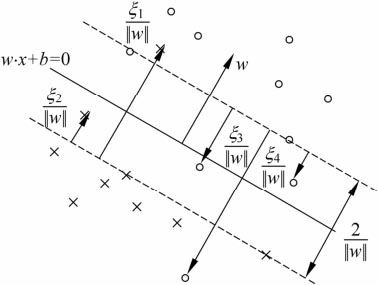
如图所示,在H1和H2上的点就是支持向量。H1和H2之间称间隔边界。
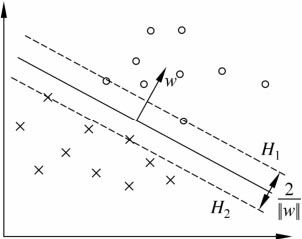
由于支持向量在确定分离超平面中起着决定性作用,所以将这种分类模型称为支持向量机 。
具体过程可对照书上例题理解。
学习的对偶算法
构建拉格朗日函数
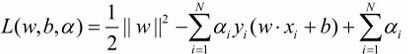
原始问题的对偶问题是极大极小问题: ![]()
(1)求 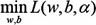
将拉格朗日函数 L(w,b,a)分别对w,b求偏导数,令为0可得:

带入拉格朗日函数 L(w,b,a),可得
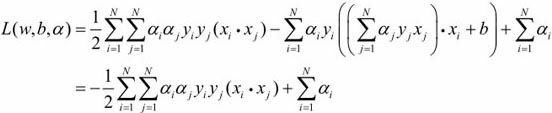
即
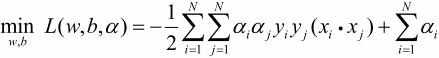
(1)求 ![]() 对a的极大。其等价的对偶最优化问题:
对a的极大。其等价的对偶最优化问题:
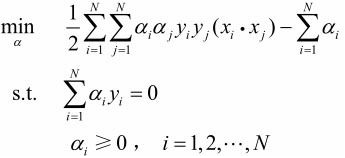
假设求出的解为a*,则原始最优化问题的解为
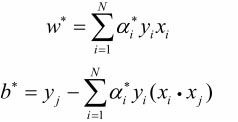
证明:根据拉格朗日对偶性,满足KKT条件
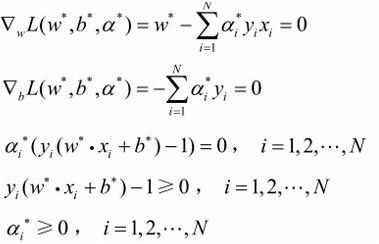
因此,分离超平面可以写成
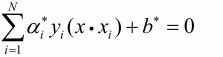

可以对比书上例题加深理解。
软间隔最大化
线性不可分意味着某些样本点(xi,yi)不能满足函数间隔大于等于1的约束条件,可以对每个样本点引入松弛变量ξi,使函数间隔加上松弛变量大于等于1。这样,约束条件为: 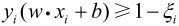
同时,对每个松弛变量支付一个代价ξi,这样目标函数变成 ![]() ,这里C>0称为惩罚参数。
,这里C>0称为惩罚参数。
最小化目标函数包含两层含义:使 ![]() 尽量小即间隔尽量大,同时使误分类点的个数尽量少,C是调和二者的系数。
尽量小即间隔尽量大,同时使误分类点的个数尽量少,C是调和二者的系数。
线性不可分的线性支持向量机的学习问题变成如下凸二次规划问题:
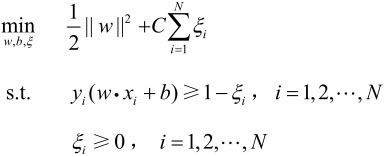
因而关于(w,b,ξ)的解是存在的。可以证明w的解是唯一的,但b的解不唯一,b的解存在于一个区间。
拉格朗日函数为(两个约束条件都是≤0):
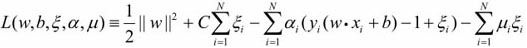
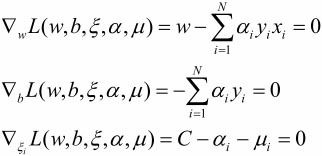 可得
可得 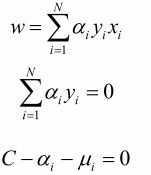 ,将其带入 L()可得:
,将其带入 L()可得:
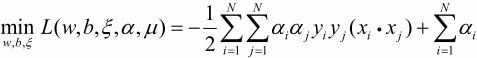
再对 ![]() 求a的极大,即得对偶问题:
求a的极大,即得对偶问题:

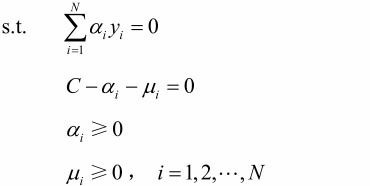
对约束条件进行处理,可以消去![]() ,只留下变量ai,这时后三个约束条件可以写成
,只留下变量ai,这时后三个约束条件可以写成  ,可得对偶问题
,可得对偶问题
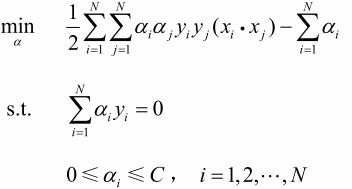
支持向量
支持向量是约束条件 ![]() 等号成立的点,间隔边界同线性可分支持向量机的间隔边界相同,即
等号成立的点,间隔边界同线性可分支持向量机的间隔边界相同,即 ![]() 等号成立的点形成的向量所围成的间隔。
等号成立的点形成的向量所围成的间隔。
软间隔的支持向量xi或者在间隔边界上,或者在间隔边界与分离超平面之间,或者在分离超平面误分一侧。
若ai* < C,则ξi= 0,支持向量xi恰好落在间隔边界上;
若ai* = C,0<ξi<1,则分类正确,xi在间隔边界与分离超平面之间;
若ai* = C,ξi= 1,xi在分离超平面上;
若ai* = C,ξi> 1,xi位于分离超平面误分一侧。
合页损失函数
线性支持向量机原始最优化问题:
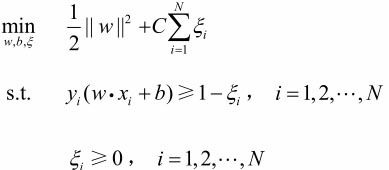
等价于最优化问题: ![]()
目标函数的第1项是经验损失或经验风险,函数 ![]() 称为合页损失函数。小标“+”有如下解释:
称为合页损失函数。小标“+”有如下解释: ![]()
这就是说,当样本点(xi,yi)被正确分类且函数间隔(确信度)yi(w·xi+b)大于1时,损失是0,否则损失是1- yi(w·xi+b)。
目标函数的第2项是系数为λ的 w 的L2范数,是正则化项。
证明: 令[1- yi(w·xi+ b)]+=[ξi]+=ξi,ξi≥0 , 所以最优化问题可以写为: ![]()
取 ![]() , 则
, 则 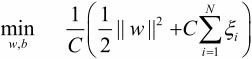 ,所以与原始最优化问题等价。
,所以与原始最优化问题等价。
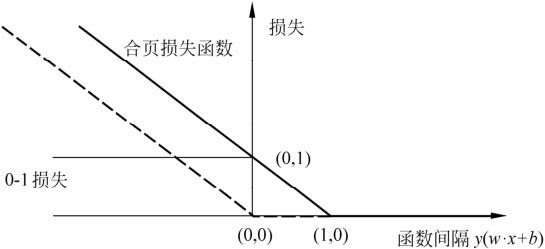
如下图,0-1损失函数可以认为是二类分类问题的真正的损失函数,而合页损失函数是0-1损失函数的上界。由于0-1损失函数不是连续可导的,直接优化由其构成的目标函数比较困难,可以认为线性支持向量机是优化由0-1损失函数的上界(合页损失函数)构成的目标函数。这时的上界损失函数又称为代理损失函数,虚线显示的是感知机的损失函数[-yi(w·xi+ b)]+ ,当样本点被正确分类时,yi(w·xi+ b)>0,损失是0,否则损失是-yi(w·xi+ b)。
相比之下,合页损失函数(直线段)不仅要分类正确,而且确信度足够高时损失才是0。也就是说,合页损失函数对学习有更高的要求。
非线性支持向量机与核函数
核技巧
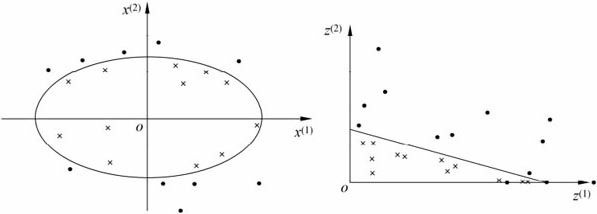
定义从原空间到新空间的变换(映射): ![]() ,原空间中的点相应地变换为新空间中的点,原空间中的椭圆
,原空间中的点相应地变换为新空间中的点,原空间中的椭圆 ![]() 变化为
变化为
新空间中的直线 ![]() ,核技巧就属于这种方法。
,核技巧就属于这种方法。
核技巧应用到支持向量机,其基本想法就是通过一个非线性变换将输入空间(欧氏空间Rn或离散集合)对应于一个特征空间(希尔伯特空间![]() ),使得在输入空间Rn中的超曲面模型对应于特征空间中的超平面模型(支持向量机)。
),使得在输入空间Rn中的超曲面模型对应于特征空间中的超平面模型(支持向量机)。
这样,分类问题的学习任务通过在特征空间中求解线性支持向量机就可以完成。
核函数:如果存在一个从输入空间x到特征空间![]() 的映射:
的映射:![]() ,使得对所有的x,z∊x,函数K(x,z)满足条件
,使得对所有的x,z∊x,函数K(x,z)满足条件 ![]() ,则称K(x,z)为核函数,Ø(x)为映射函数,式中Ø(x)·Ø(z)为Ø(x)和Ø(z)的内积。
,则称K(x,z)为核函数,Ø(x)为映射函数,式中Ø(x)·Ø(z)为Ø(x)和Ø(z)的内积。
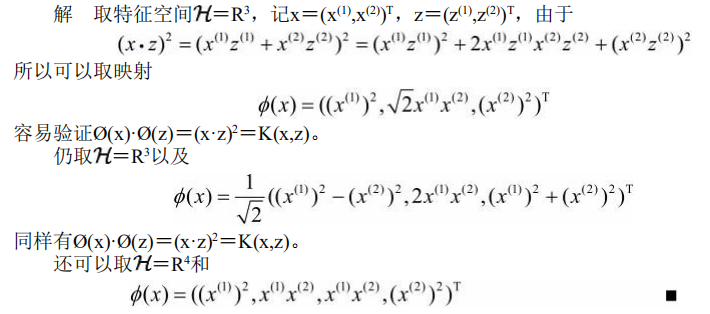
核技巧在支持向量机中的应用

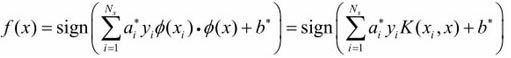
正定核
设K是对称函数,则K(x,z)为正定核函数的充要条件是对任意x,K(x,z)对应的Gram矩阵: ![]() 是半正定矩阵。
是半正定矩阵。
必要性:由于K(x,z)是正定核,则 ![]() ,构造K(x,z)的Gram矩阵
,构造K(x,z)的Gram矩阵 ![]() ,有
,有

表明K(x,z)的Gram矩阵是半正定的。
充分性:已知K(x,z)的Gram矩阵是半正定的,构造映射 ![]() ,有
,有 ![]() ,所以
,所以 ![]()
表明K(x,z)是核函数。
对于一个具体函数K(x,z)来说,不容易检验它是否为正定核函数,可以验证K对应的Gram矩阵是否半正定。
常用核函数
1. 多项式核函数: ![]() ,对应的支持向量机是一个p次多项式分类器。在此情形下,分类决策函数成为
,对应的支持向量机是一个p次多项式分类器。在此情形下,分类决策函数成为
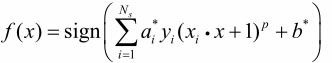
2. 高斯核函数: ![]() ,对应的支持向量机是高斯径向基函数分类器。在此情形下,分类决策函数成为
,对应的支持向量机是高斯径向基函数分类器。在此情形下,分类决策函数成为
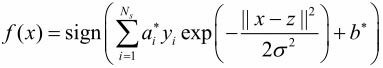
3. 字符串核函数: 核函数同样也可以定义在离散数据的集合上,参考理解字符串核函数。
假设H3的一维对应于字符串asd,这时,字符串“Nasdaq”与“lass das”在这一维上的值分别是[Ø3(Nasdaq)]asd=λ3 和[Ø3(lass□das)]asd=2λ5(□为空格)。在第1个字符串里,asd是连续的子串。在第2个字符串里,asd是长度为5的不连续子串,共出现2次:lass das和lass das。
两个字符串s和t上的字符串核函数是基于映射 Øn 的特征空间中的内积:
![]()
直观上,两个字符串相同的子串越多,它们就越相似,字符串核函数的值就越大。字符串核函数可以由动态规划快速地计算。
非线性支持向量分类机
将线性支持向量机扩展到非线性支持向量机,只需将线性支持向量机对偶形式中的内积换成核函数。
最优化问题为:
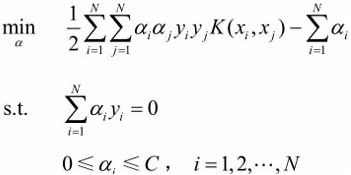
序列最小最优化算法
是当训练样本容量很大时,前边的算法往往会很低效,为了高效地实现支持向量机学习,可以采用序列最小最优化(SMO)算法。
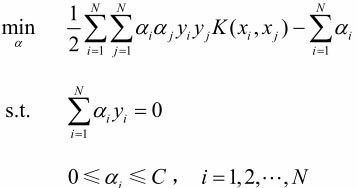
两个变量二次规划的求解方法
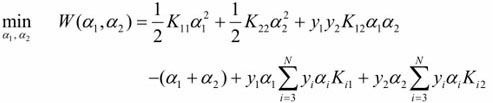
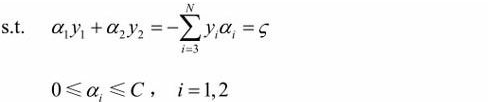
原目标函数中 ![]() ,只需要考虑a1,a2两个变量即可,因为从a3开始都是常量,对于求 min 没有影响,可以去掉。
,只需要考虑a1,a2两个变量即可,因为从a3开始都是常量,对于求 min 没有影响,可以去掉。
由于只有两个变量(a1,a2),约束可以用二维空间中的图形表示,由于等式约束,使得两个变量的最优化问题成为实质上的单变量的最优化问题(最优解必须在图中虚线线段上),不妨考虑为变量a2的最优化问题。
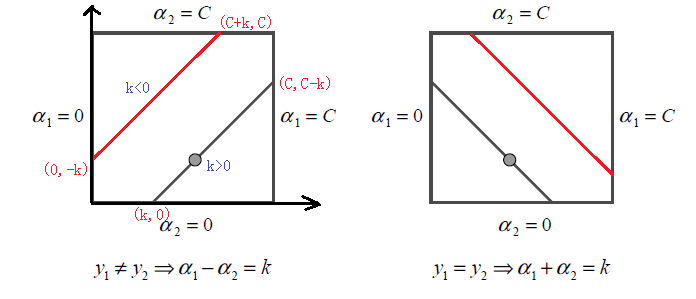
假设问题的初始可行解为![]() ,
,  ,最优解为
,最优解为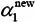 ,
,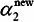 ,并且假设在沿着约束方向未经剪辑时a2的最优解为
,并且假设在沿着约束方向未经剪辑时a2的最优解为 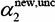
假设L和H分别是上图中![]() 所在的线段的边界。那么很显然我们有:
所在的线段的边界。那么很显然我们有: ![]() ,
,
如果是左图中的情况: 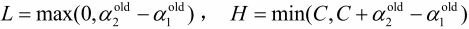
如果是右图中的情况: 
那么,最终的![]() 应该是:
应该是:
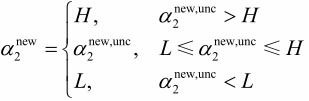
我们只需要将目标函数对a2求偏导数即可得到![]() ,
,
令 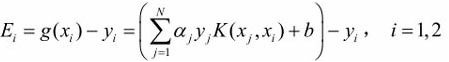 ,引进
,引进 
目标函数可写成 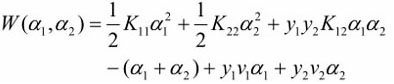
由于 a1y1 + a2y2 = ς,并且yi2=1,可以得到:![]()
可以得到只含a2的目标函数
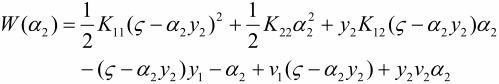
对a2求偏导数,可得
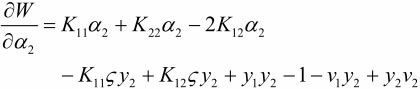
令为0,得到

将a1y1 + a2y2 = ς代入,可得
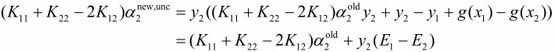
变形可得
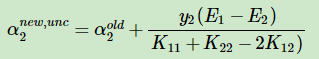
变量的选择方法
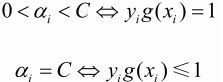
SMO选择第2个变量的过程为内层循环,假设在外层循环中已经找到第1个变量,在内层循环中,希望找到第二个变量,使 ![]() 有足够大的变化。因为a1确定,E1也随之确定,
有足够大的变化。因为a1确定,E1也随之确定,![]() 只和a2有关。
只和a2有关。
每次完成两个变量的优化之后,都要重新计算阈值b。当0< ![]() <C时,由KKT条件可知(即上述外层循环中的第二个条件,此时支持向量点在间隔边界上):
<C时,由KKT条件可知(即上述外层循环中的第二个条件,此时支持向量点在间隔边界上): ![]()
于是:
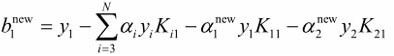
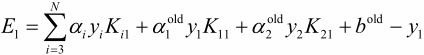
两式结合可得: 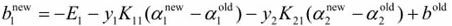
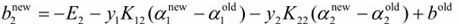
如果 ![]() ,
,![]() 同时满足0<
同时满足0< ![]() < C,两点在间隔边界上,由
< C,两点在间隔边界上,由 ![]() 可得 E1=E2=0,所以
可得 E1=E2=0,所以 ![]() =
=![]() =bnew 。不同时满足时,取
=bnew 。不同时满足时,取 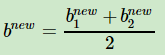 ,
,
然后更新E:
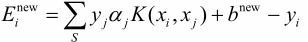
其中,S是所有支持向量xj的集合。