数据可视化
上篇文章介绍了线性不可分和线性可分两种情况,以及五种核函数,线性核函数(linear),多项式核函数(poly),高斯核函数(rbf),拉普拉斯核函数(laplace)和Sigmoid核函数,基于《机器学习实战》的数据,我们使用各种核函数对数据尝试分类,下面看一下效果如何.
首先看一下我们的数据集:
这里共有100个数据点,分类标签也是{-1,+1},但与之前不同的是,这里的数据在二维空间线性不可分.先用python看一下这些数据的分布情况.下面就是基本的读取文件和分类画点,第一类为红色,第二类为蓝色.
filename = 'testSetRBF.txt'
fr = open(filename)
X1 = [];y1 = []
X2 = [];y2 = []
for line in fr.readlines():
lineArr = line.strip().split('\t')
if float(lineArr[-1]) == 1:
X1.append(lineArr[0])
y1.append(lineArr[1])
elif float(lineArr[-1]) == -1:
X2.append(lineArr[0])
y2.append(lineArr[1])
plt.scatter(X1[:],y1[:],c='r',s=50)
plt.scatter(X2[:],y2[:],c='b',s=50)
plt.show()
与异或问题相似,数据中的点无法线性划分,所以我们引入核函数进行分类.但因为高维映射空间的未知,这类数据划分一般不太容易直观像线性可分情况一样得到可视化的超平面.
读取文件
from numpy import *
from time import sleep
import matplotlib.pyplot as plt
def loadDataSet(fileName):
dataMat = []; labelMat = []
fr = open(fileName)
for line in fr.readlines():
lineArr = line.strip().split('\t')
dataMat.append([float(lineArr[0]), float(lineArr[1])])
labelMat.append(float(lineArr[2]))
return dataMat,labelMatloadDateSet函数读取数据集,这里不多赘述.
随机选择J
def selectJrand(i,m):
j=i #希望alpha的标号不同
while (j==i):
j = int(random.uniform(0,m))
return j
selectJrand函数根据i,选择与i不同的角标作为另一个alpha的角标.
调整Alpha
def clipAlpha(aj,H,L):
if aj > H:
aj = H
if L > aj:
aj = L
return aj
根据不同的yi,调整alphaj的范围.参考(4).
转换核函数
def kernelTrans(X, A, kTup): #通过数据计算转换后的核函数
m,n = shape(X)
K = mat(zeros((m,1)))
if kTup[0]=='lin': #线性核函数
K = X * A.T
elif kTup[0]=='rbf':#高斯核
for j in range(m):
deltaRow = X[j,:] - A
K[j] = deltaRow*deltaRow.T
K = exp(K/(-1*kTup[1]**2))
elif kTup[0] == 'laplace':#拉普拉斯核
for j in range(m):
deltaRow = X[j,:] - A
K[j] = deltaRow*deltaRow.T
K[j] = sqrt(K[j])
K = exp(-K/kTup[1])
elif kTup[0] == 'poly':#多项式核
K = X * A.T
for j in range(m):
K[j] = K[j]**kTup[1]
elif kTup[0] == 'sigmoid':#Sigmoid核
K = X * A.T
for j in range(m):
K[j] = tanh(kTup[1]*K[j]+kTup[2])
else: raise NameError('执行过程出现问题 -- \
核函数无法识别')
return K
根据(6)的数学公式得到的五种核函数的表达形式,在获取数据集的情况下,实现数据转核矩阵.一会针对上述数据集,我们可以看到对于这样线性不可分的数据集,采用lin线性核的效果将大打折扣,而高斯核,拉普拉斯核的效果比较满意.
数据结构
class optStruct:
def __init__(self,dataMatIn, classLabels, C, toler, kTup): # Initialize the structure with the parameters
self.X = dataMatIn
self.labelMat = classLabels
self.C = C
self.tol = toler
self.m = shape(dataMatIn)[0]
self.alphas = mat(zeros((self.m,1)))
self.b = 0
self.eCache = mat(zeros((self.m,2))) #first column is valid flag
self.K = mat(zeros((self.m,self.m)))
for i in range(self.m):
self.K[:,i] = kernelTrans(self.X, self.X[i,:], kTup)
为了算法的一致性与简洁性,这里定义了数据结构,之后的函数调用都采用以上的数据结构,从而提高了效率.
计算误差E
def calcEk(oS, k):
fXk = float(multiply(oS.alphas,oS.labelMat).T*oS.K[:,k] + oS.b)
Ek = fXk - float(oS.labelMat[k])
return Ek
这里根据公式E = f(xi) - yi ,负责计算误差E.
根据最大误差选取J
def selectJ(i, oS, Ei):
maxK = -1; maxDeltaE = 0; Ej = 0
oS.eCache[i] = [1,Ei]
validEcacheList = nonzero(oS.eCache[:,0].A)[0]
# print(validEcacheList)
if (len(validEcacheList)) > 1:
for k in validEcacheList:
if k == i: continue
Ek = calcEk(oS, k)
deltaE = abs(Ei - Ek)
if (deltaE > maxDeltaE):
maxK = k; maxDeltaE = deltaE; Ej = Ek
return maxK, Ej
else: #in this case (first time around) we don't have any valid eCache values
j = selectJrand(i, oS.m)
Ej = calcEk(oS, j)
return j, Ej
直观来看,KKT条件违背的程度越大,则更新变量更新后可能导致的目标函数增幅越大,所以SMO算法先选取违背KKT条件最大的变量,第二个变量的选择一个使目标函数值增长最快的变量。这里SMO采用了一种启发式,是选取的两个变量所对应的样本的间隔最大,一种直观的解释,这样的两个变量有很大的区别,与对两个相似变量更新相比,对他们更新会使目标函数值发生更大的变化.(参考西瓜书)
更新误差E
def updateEk(oS, k):
Ek = calcEk(oS, k)
oS.eCache[k] = [1,Ek]在alpha更新后,其相对应的误差E也基于更新的alpha重新计算.
SMO算法
def innerL(i, oS):
Ei = calcEk(oS, i)
if ((oS.labelMat[i]*Ei < -oS.tol) and (oS.alphas[i] < oS.C)) or ((oS.labelMat[i]*Ei > oS.tol) and (oS.alphas[i] > 0)):
j,Ej = selectJ(i, oS, Ei)
alphaIold = oS.alphas[i].copy(); alphaJold = oS.alphas[j].copy();
if (oS.labelMat[i] != oS.labelMat[j]):
L = max(0, oS.alphas[j] - oS.alphas[i])
H = min(oS.C, oS.C + oS.alphas[j] - oS.alphas[i])
else:
L = max(0, oS.alphas[j] + oS.alphas[i] - oS.C)
H = min(oS.C, oS.alphas[j] + oS.alphas[i])
if L==H: print ("L==H"); return 0
eta = 2.0 * oS.K[i,j] - oS.K[i,i] - oS.K[j,j]
if eta >= 0: print ("eta>=0"); return 0
oS.alphas[j] -= oS.labelMat[j]*(Ei - Ej)/eta
oS.alphas[j] = clipAlpha(oS.alphas[j],H,L)
updateEk(oS, j)
if (abs(oS.alphas[j] - alphaJold) < 0.00001): print ("j not moving enough"); return 0
oS.alphas[i] += oS.labelMat[j]*oS.labelMat[i]*(alphaJold - oS.alphas[j])
updateEk(oS, i)
b1 = oS.b - Ei- oS.labelMat[i]*(oS.alphas[i]-alphaIold)*oS.K[i,i] - oS.labelMat[j]*(oS.alphas[j]-alphaJold)*oS.K[i,j]
b2 = oS.b - Ej- oS.labelMat[i]*(oS.alphas[i]-alphaIold)*oS.K[i,j]- oS.labelMat[j]*(oS.alphas[j]-alphaJold)*oS.K[j,j]
if (0 < oS.alphas[i]) and (oS.C > oS.alphas[i]): oS.b = b1
elif (0 < oS.alphas[j]) and (oS.C > oS.alphas[j]): oS.b = b2
else: oS.b = (b1 + b2)/2.0
return 1
else: return 0
这里是基本的SMO算法实现步骤,具体过程不再赘述,可以参考(2),(5).
核函数选择并计算参数alpha,b
def smoP(dataMatIn, classLabels, C, toler, maxIter,kTup=('rbf', 1.3)):
oS = optStruct(mat(dataMatIn),mat(classLabels).transpose(),C,toler, kTup)
iter = 0
entireSet = True; alphaPairsChanged = 0
while (iter < maxIter) and ((alphaPairsChanged > 0) or (entireSet)):
alphaPairsChanged = 0
if entireSet:
for i in range(oS.m):
alphaPairsChanged += innerL(i,oS)
print ("fullSet, iter: %d i:%d, pairs changed %d" % (iter,i,alphaPairsChanged))
iter += 1
else:
nonBoundIs = nonzero((oS.alphas.A > 0) * (oS.alphas.A < C))[0]
for i in nonBoundIs:
alphaPairsChanged += innerL(i,oS)
print ("non-bound, iter: %d i:%d, pairs changed %d" % (iter,i,alphaPairsChanged))
iter += 1
if entireSet: entireSet = False
elif (alphaPairsChanged == 0): entireSet = True
print ("iteration number: %d" % iter)
return oS.b,oS.alphas
根据输入的数据集,标签,松弛因子C,容忍度toler,最大迭代数与核函数参数,运行完整的SMO算法,直到更新达到一定条件(达到迭代最大次数,更新程度达到一定变化范围),停止迭代,返回参数alpha,b.
计算系数W
def calculateW(alphas,dataArr,labelArr):
alphas, dataMat, labelMat = array(alphas), array(dataArr), array(labelArr)
sum = 0
for i in range(shape(dataMat)[0]):
sum += alphas[i]*labelMat[i]*dataMat[i].T
print(sum)
return sum
通过上一个函数返回的alpha,b,通过拉格朗日法推出的w公式,计算w,参考(6).
测试函数
def testRbf(k1=1.3):
dataArr,labelArr = loadDataSet('testSetRBF.txt')
b,alphas = smoP(dataArr, labelArr, 200, 0.0001, 10000, ('rbf', k1))
datMat=mat(dataArr); labelMat = mat(labelArr).transpose()
svInd=nonzero(alphas.A>0)[0]
sVs=datMat[svInd]
labelSV = labelMat[svInd];
print ("there are %d Support Vectors" % shape(sVs)[0])
m,n = shape(datMat)
errorCount = 0
for i in range(m):
kernelEval = kernelTrans(sVs,datMat[i,:],('rbf', k1))
predict=kernelEval.T * multiply(labelSV,alphas[svInd]) + b
if sign(predict)!=sign(labelArr[i]): errorCount += 1
print ("the training error rate is: %f" % (float(errorCount)/m))
dataArr,labelArr = loadDataSet('testSetRBF2.txt')
errorCount = 0
datMat=mat(dataArr); labelMat = mat(labelArr).transpose()
m,n = shape(datMat)
for i in range(m):
kernelEval = kernelTrans(sVs,datMat[i,:],('rbf', k1))
predict=kernelEval.T * multiply(labelSV,alphas[svInd]) + b
if sign(predict)!=sign(labelArr[i]): errorCount += 1
print ("the test error rate is: %f" % (float(errorCount)/m))
这里选择参数sigma=2,rbf 高斯核函数对之前的线性不可分点进行分类,根据预测标签与真实标签的判别,计算分类的错误率.这里可以修改核函数参数,选择不同的核函数看看支持向量机的性能表现.
标记支持向量
def plot_point(filename,alphas,dataMat):
filename = filename
fr = open(filename)
X1 = [];y1 = []
X2 = [];y2 = []
for line in fr.readlines():
lineArr = line.strip().split('\t')
if float(lineArr[-1]) == 1:
X1.append(lineArr[0])
y1.append(lineArr[1])
elif float(lineArr[-1]) == -1:
X2.append(lineArr[0])
y2.append(lineArr[1])
plt.scatter(X1[:],y1[:],c='y',s=50)
plt.scatter(X2[:],y2[:],c='b',s=50)
for i, alpha in enumerate(alphas):
if abs(alpha) > 0:
x, y = dataMat[i]
plt.scatter(x, y, s=100, c = '', alpha=0.5, linewidth=1.5, edgecolor='red')
plt.show()
通过KKT条件,寻找alpha大于0的alpha作为支持向量,然后将对应点标记.
主函数
if __name__ == "__main__":
dataArr,labelArr = loadDataSet('testSetRBF.txt')
b,alphas = smoP(dataArr,labelArr,0.6,0.001,40)
testRbf()
plot_point('testSetRBF.txt',alphas,dataArr)
calculateW(alphas,dataArr,labelArr)
第一行读取数据,第二行根据参数计算alpha,b,第三行计算错误率,第四行标记支撑向量,最后一行计算W.
看一下rbf高斯核,k=1.3的分类效果:
there are 31 Support Vectors the training error rate is: 0.020000 the test error rate is: 0.030000 w = [-0.1685502 -0.1276386] [Finished in 18.8s]
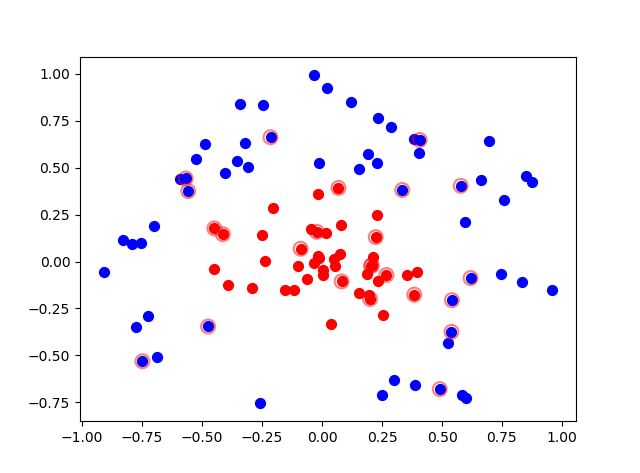
修改为lapalace拉普拉斯核,k=1.3的分类效果(在testrbf函数中依据前面的核函数选择修改参数即可):
there are 31 Support Vectors the training error rate is: 0.000000 the test error rate is: 0.200000 w = [-0.436887 -0.9289236] [Finished in 24.4s]
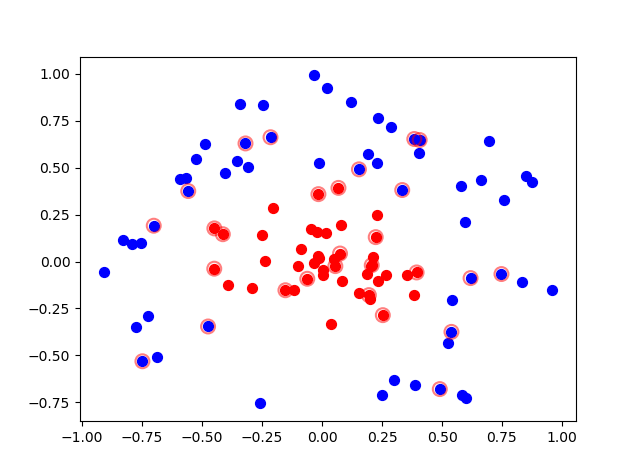
可以看到lapalace核的训练集样本准确率很高,但是测试集准确率不高,说明模型存在过拟合,这与参数的选择也有很大关系,可以调节K1(sigma),寻找最优的核函数参数.
修改为linear核(没计算就猜到准确率会很低):
there are 69 Support Vectors the training error rate is: 0.330000 the test error rate is: 0.490000 w = [ 0.0532572 -0.3009696] [Finished in 19.1s]
可以看到线性分类器对非线性可分的样本分类效果很差,虽然有二倍于之前的支持向量,但测试集分类效果已经和随机猜测概率接近一致,所以说支持向量机的性能好坏并不决定于支持向量的数量.
总结:
还有两种核函数这里没有尝试,大家有兴趣可以自己修改,看看错误率表现如何,支持向量机的准确率和核函数的选择,参数的选择等等都有关系,所以多调参数,才能找到最理想的分类效果,而我们也看到,支持向量大多数都分布在边界处,这里也只能脑补一下他们在高维的分割超平面了.《机器学习实战》上关于SVM的大概就这么多了,接下来将运用Sklearn库,实现支持向量机分类的简易实现和超平面的绘制.有问题欢迎大家交流~

