在算法竞赛中,博弈论题目往往是以icg。通俗的说就是两人交替操作,每步都各自合法,合法性与选手无关,只与游戏有关。往往我们需要求解在某一个游戏或几个游戏中的某个状态下,先手或后手谁会胜利的问题。就比如经典的:几堆石子,两人可以分别拿若干个,一次只能选择一个石子堆操作,问给定状态下,先手胜利还是后手胜利?
而nim与sg函数就是对于这类问题的解法,在我的理解看来,sg函数和nim分别对应不同阶段的决策:前者对于单个游戏决策,后着是将这些单个游戏综合起来的整体决策。
一、状态与转移
icg游戏往往可以分为两个部分,规则与局面。而这两个分别对应了转移与状态。规则决定了状态转移的合法性,状态是转移的基本。
什么是状态?状态是一个静态的局面。就好比当下棋时的局面一样。在游戏的每个阶段,不论是开始,中间,或是结束。每一个局面都对应了一种状态。
什么是状态的转移?单个分开的局面无法构成一个完整的游戏,所以就需要从某一个状态转移到另一个状态,来进行一次操作。
举个例子:有5个石子放在一堆。
5个石子就是一种状态,在不受限制下,你可以改变这个状态。
例如:取走4个石子。就是将5个石子这个状态转移到1个石子这个状态,操作就是取走4个石子。
而这个操作的合法性取决于游戏的规则。
例如:一次最多取3个石子。 那么上条操作取4个石子就是一次不合法的操作,意味着你不能从5这个状态直接转移到1这个状态。
那么对于5个石子,每次最多取三个,从中我们可以得到如下状态转移的图(有向)
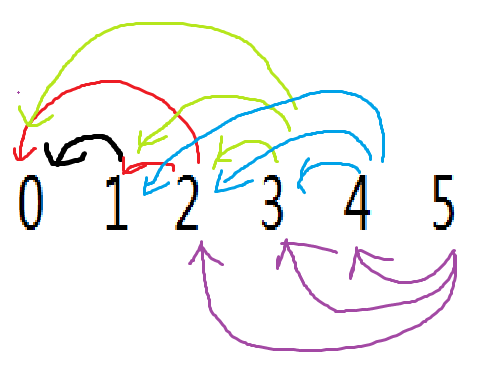
二、sg函数
概念
首先,引入mex值的概念。mex是指不属于集合中整数的最小正整数。而sg值就是不属于后继集合的最小正整数。
例如上图中:0没有后继元素 所以最小正整数为0,sg(0)=0;
1后继元素只有0,不属于后继集合的最小正整数为1,sg(1)=1;
同理可得sg(2)=2;sg(3)=3;
到4的时候,情况就发生了变化。由于4不能直接转移到1,故后继集合只有{1,2,3},sg(4)=0;
这里的状态用1,2,3,4之类是为了举例,而实际上状态不一定是这样转换,可能有很多种状态,不仅仅局限于单个数字,亦可以是某种局面,某个棋盘局面,某个路径局面,如果能找到”状态“只要这个游戏没有循环,在有限步数可以达到结果,就可以对这个游戏的每个状态求出sg值。
求解
求解顺序是这样的。首先找到所有的结尾局面。比如取石子游戏中的石子剩余为0,或是棋盘游戏中棋子的无路可走,所以这些状态的sg值都为0,然后从这个状态逆向求他的前驱,求出所有前驱的sg值。 如果了解过拓扑排序,那么很容易理解这个过程。用拓扑排序来讲就是一个状态的后继sg值没有确定时,这个状态的sg值也无法确定。故从所有无路可走的局面按照逆向的拓扑排序过程就可以求出所有可达状态的sg值。
意义
求出了sg值后,对于解这个游戏胜负关系有什么用呢?
由上面的概念我们可以得到两个结论
- sg值为0的状态,前一状态一定全是非0状态。(一定全是非0状态)
- sg值为非零的状态,一定能一步转移到0状态(不一定必须转到,是可以转到)
由此我们可以进行决策。
如果我们先手是非零,我们可以始终选择一步转移到sg值为0的状态,那么下一家一定只能转移到非0。那么到你又可以一步转移到0。循环如此决策,就可以让下一家最终转移到败态的0状态处,从而获得胜利
如果我们先手是零,那么我们只能转移到非0状态,下一家可以用以上必胜决策进行操作,那么我们就必败。
由此我们得到sg值与胜利与失败的关系。
sg(此状态)=0时,先手的人必败。即(此状态)为必败态
sg(此状态)≠0时,先手的人必胜。即(此状态)为必败态
sg函数可以看做在这个游戏下规则的体现,可以直接反映出转移的方式。而sg()函数某个值可以视作某个状态下的胜负情况。
往往一个游戏需要求的只是一个局面下的胜负情况。即一个sg(a),但实际运用中需要通过求出每个中间态的sg值来推出所需状态的sg值。是不是有点动态规划的思想?
三、nim博弈
然而,一个游戏可能由多个状态共同构成,即两个状态间不能互相影响或转移到同一个末状态。这时单纯的sg函数就不够解题了。因此我们引入了一个多游戏间的决策,nim博弈。对于多个游戏间的博弈,不能用简单的sg函数表达。可以把这个复合的游戏进行转变,成为多个互不影响的游戏,即每个游戏可以各自求出各自的sg函数,解出各自状态对应的sg值。将多个游戏+状态的sg值综合起来的方式,即为nim。
求解方式是res=sg[1]^sg[2]^sg[3]^...^sg[n]。即为这些游戏组合在一起后,整体的胜负态。
右方sg值对应的是那个游戏的起始状态的sg值。
(sg补充)sg值不用单纯的0和非0来表示的原因:
多个游戏中,比如两个游戏,一个是必胜态,一个是必败态。如果按照单个游戏都要必胜的策略玩在一个游戏结束时,再玩下一个游戏,相当于先后手对调,先手必败。但是先手可以将某一个的状态从非零依旧转移到非零,从而改变整体胜负态,比如从sg=2转移到sg=1,对手无法再扭转回来,自己就可以获胜。但是如果sg更大,那么双方会持续做这个抉择。这个抉择是有尽头的,到这个尽头时的状态就决定了最后整体胜负态,这个决策可执行的次数就是sg值的数量,比如sg=5时,最多可以多转移4次(然而转移四次不是一定最佳选择,读者可以进行模拟思考) 因此sg值要取具体值,在异或的时候各自的信息也提供了用处。
nim的决策公式推出的多个游戏组合后的值,就对应了整体的胜负态。
四、例题
HDU-1524 A-chess-game
两者综合运用多个棋子分别看待,对应两个独立的游戏,拓扑排序,然后求出每个局面打表求出对应的sg值。
由于在同一套规则上,所以可以用同一个sg函数。将所有起始局面的sg值异或起来,根据是否为0求出结果
代码如下

1 #include<iostream> 2 #include<vector> 3 #include<cstring> 4 using namespace std; 5 6 struct point{ 7 int sg=0; 8 vector <int> out; 9 vector <int> in; 10 int inn=0; 11 int sgg=0; 12 }graph[10005]; 13 bool num[100005]; 14 int mex(int x) 15 { 16 memset(num,0,sizeof(num)); 17 for(int i=0;i<graph[x].in.size();i++){ 18 num[graph[graph[x].in[i]].sg]=1; 19 } 20 for(int i=0;i<10005;i++){ 21 if(num[i]==0)return i; 22 } 23 } 24 void get_sg(int n) 25 { 26 for(int i=0;i<n;i++){ 27 for(int i=0;i<n;i++){ 28 if(graph[i].inn==0&&graph[i].sgg==0){ 29 graph[i].sg=mex(i); 30 graph[i].sgg=1; 31 for(int j=0;j<graph[i].out.size();j++){ 32 graph[graph[i].out[j]].inn--; 33 } 34 } 35 } 36 } 37 } 38 int main() 39 { 40 int n,m,a; 41 while(cin>>n){ 42 for(int i=0;i<=n;i++){ 43 graph[i].out.clear(); 44 graph[i].in.clear(); 45 graph[i].sg=0; 46 graph[i].inn=0; 47 graph[i].sgg=0; 48 } 49 for(int i=0;i<n;i++){ 50 cin>>m; 51 for(int j=0;j<m;j++){ 52 cin>>a; 53 graph[i].in.push_back(a); 54 graph[a].out.push_back(i); 55 graph[i].inn++; 56 } 57 } 58 get_sg(n); 59 int res=0; 60 while(cin>>m){ 61 if(m==0)break; 62 res=0; 63 for(int i=0;i<m;i++){ 64 cin>>a; 65 res^=graph[a].sg; 66 } 67 if(res!=0)cout<<"WIN"<<endl; 68 else cout<<"LOSE"<<endl; 69 } 70 } 71 }
POJ-2960 S-Nim
从0开始,对逆向根据规则对每个状态打表,求出sg值(如果某个点求过了,就不要重复求),再根据nim将多个结果异或起来

1 #include<iostream> 2 #include<cstring> 3 using namespace std; 4 int sg[10005]; 5 int s[10005]; 6 bool num[10005]; 7 int n,m; 8 int mex(int x){ 9 memset(num,0,sizeof(num)); 10 for(int i=0;i<n;i++){ 11 if(x-s[i]>=0){ 12 num[sg[x-s[i]]]=1; 13 } 14 } 15 for(int i=0;i<10005;i++){ 16 if(num[i]==0)return i; 17 } 18 return -1; 19 } 20 int get_sg(){ 21 for(int i=0;i<10005;i++){ 22 sg[i]=mex(i); 23 } 24 } 25 int main() 26 { 27 int T ; 28 int p,q; 29 while (cin >> n) { 30 memset(sg,0,sizeof(sg)); 31 if (n == 0) break; 32 for (int i = 0; i < n; i ++)cin >> s[i]; 33 get_sg(); 34 cin >> m; 35 36 while (m--){ 37 int res = 0; 38 cin>>q; 39 for(int i=0;i<q;i++){ 40 cin >> p; 41 res ^= sg[p]; 42 } 43 if(res==0)cout<<"L"; 44 else cout<<"W"; 45 } 46 cout<<endl; 47 } 48 return 0; 49 }
如有疑问或异议,欢迎私信博主进行讨论与交流
