EM算法
EM算法主要用于求概率密度函数参数的最大似然估计,将问题$\arg \max _{\theta_{1}} \sum_{i=1}^{n} \ln p\left(x_{i} | \theta_{1}\right)$转换为更加易于计算的$\sum_{i=1}^{n} \ln p\left(x_{i}, \theta_{2} | \theta_{1}\right)$,其中$\theta_2$可以取任意的先验分布$q(\theta_2)$。EM算法的推导过程如下:$$\begin{aligned} \ln p\left(x | \theta_{1}\right) &=\int q\left(\theta_{2}\right) \ln p\left(x | \theta_{1}\right) d \theta_{2}=\int q\left(\theta_{2}\right) \ln \frac{p\left(x, \theta_{2} | \theta_{1}\right)}{p\left(\theta_{2} | x, \theta_{1}\right)} d \theta_{2}=\int q\left(\theta_{2}\right) \ln \frac{p\left(x, \theta_{2} | \theta_{1}\right) q\left(\theta_{2}\right)}{p\left(\theta_{2} | x, \theta_{1}\right) q\left(\theta_{2}\right)} d \theta_{2} \\ &=\underbrace{\int q\left(\theta_{2}\right) \ln \frac{p\left(x, \theta_{2} | \theta_{1}\right)}{q\left(\theta_{2}\right)} d \theta_{2}}_{\text { define this to }\mathcal{L}\left(x,\theta_1\right)}+\underbrace{\int q\left(\theta_{2}\right) \ln \frac{q\left(\theta_{2}\right)}{p\left(\theta_{2} | x, \theta_{1}\right)} d \theta_{2}}_{\text { Kullback-Leibler divergence }} \end{aligned}$$利用凸函数的性质,$\text{KL divergence}=E\left[-\ln \frac{p\left(\theta_{2} | x, \theta_{1}\right)}{q\left(\theta_{2}\right)}\right]\geq{-\ln{E\left[\frac{p\left(\theta_{2} | x, \theta_{1}\right)}{q\left(\theta_{2}\right)}\right]}}=-\ln{1}=0$,当且仅当$q\left(\theta_{2}\right)=p\left(\theta_{2} | x, \theta_{1}\right)$时$\text{KL divergence}$取值为0。
基于以上推导,EM算法的计算流程如下:
给定初始值$\theta_1^{(0)}$,按以下步骤迭代至收敛(以第t+1步为例):
- E-step: 令$q_{t}\left(\theta_{2}\right)=p\left(\theta_{2} | x, \theta_{1}^{(t)}\right)$,则$\mathcal{L}_{t}\left(x, \theta_{1}\right)=\int q_{t}\left(\theta_{2}\right) \ln p\left(x, \theta_{2} | \theta_{1}\right) d \theta_{2}-\underbrace{\int q_{t}\left(\theta_{2}\right) \ln q_{t}\left(\theta_{2}\right) d \theta_{2}}_{\text { can ignore this term }}$
- M-step: 令$\theta_{1}^{(t+1)}=\arg \max _{\theta_{1}} \mathcal{L}_{t}\left(x, \theta_{1}\right)$
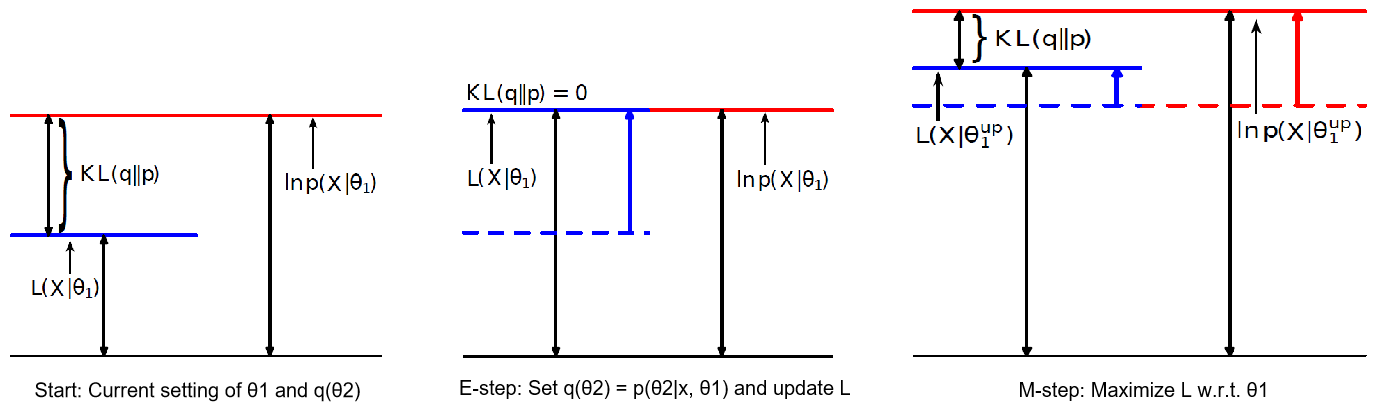
算法解释:
$$
\begin{aligned} \ln p\left(x | \theta_{1}^{(t)}\right) &=\mathcal{L}_{t}\left(x, \theta_{1}^{(t)}\right)+\underbrace{K L\left(q_t\left(\theta_{2}\right) \| p\left(\theta_{2} | x_{1}, \theta_{1}^{(t)}\right)\right)}_{=0 \text { by setting } q=p}\quad \leftarrow \text { E-step } \\ & \leq \mathcal{L}_{t}\left(x, \theta_{1}^{(t+1)}\right) \quad \leftarrow \text { M-step } \\ & \leq \mathcal{L}_{t}\left(x, \theta_{1}^{(t+1)}\right)+\underbrace{K L\left(q_{t}\left(\theta_{2}\right) \| p\left(\theta_{2} | x_{1}, \theta_{1}^{(t+1)}\right)\right)}_{>0 \text { because } q \neq p} \\ &=\ln p\left(x | \theta_{1}^{(t+1)}\right)\end{aligned}
$$
高斯混合模型GMM
高斯混合模型是一个用于聚类的概率模型,对于数据$\vec{x}_1,\vec{x}_2,\cdots,\vec{x}_n$中的任一数据$\vec{x}_i$,$c_i$表示$\vec{x}_i$被分配到了第$c_i$个簇中,并且$c_i\in\{1,2,\cdots,K\}$。模型定义如下:
- Prior cluster assignment: $c_{i} \stackrel{\text { iid }}{\sim}$ Discrete $(\vec{\pi}) \Rightarrow \operatorname{Prob}\left(c_{i}=k | \vec{\pi}\right)=\pi_{k}$
- Generate observation: $\vec{x}_i \sim N\left(\vec{\mu}_{c_{i}}, \Sigma_{c_{i}}\right)$
模型需要求解的就是先验概率$\vec{\pi}=(\pi_1,\pi_2,\cdots,\pi_K)$,各簇高斯分布的均值$\{\vec{\mu}_1,\vec{\mu}_2,\cdots,\vec{\mu}_K\}$以及协方差矩阵$\{\Sigma_1,\Sigma_2,\cdots,\Sigma_K\}$这些量。为了求解这些量,使用最大似然估计,定义需最大化的目标函数为
$$\sum_{i=1}^{n} \ln p\left(\vec{x}_{i} | \vec{\pi}, \boldsymbol{\mu}, \boldsymbol{\Sigma}\right)\text{, where }\boldsymbol{\mu}=\{\vec{\mu}_1,\vec{\mu}_2,\cdots,\vec{\mu}_K\}\text{ and }\boldsymbol{\Sigma}=\{\Sigma_1,\Sigma_2,\cdots,\Sigma_K\}$$
利用EM算法求解上式的最大值,将上式写为$$\sum_{i=1}^{n} \ln p\left(\vec{x}_{i} | \vec{\pi}, \boldsymbol{\mu}, \boldsymbol{\Sigma}\right)=\sum_{i=1}^{n} \underbrace{\sum_{k=1}^{K} q\left(c_{i}=k\right) \ln \frac{p\left(\vec{x}_{i}, c_{i}=k | \vec{\pi}, \boldsymbol{\mu}, \boldsymbol{\Sigma}\right)}{q\left(c_{i}=k\right)}}_{\mathcal{L}}+\sum_{i=1}^n\underbrace{\sum_{k=1}^{K} q\left(c_{i}=k\right) \ln \frac{q\left(c_{i}=k\right)}{p\left(c_{i}=k | \vec{x}_{i}, \vec{\pi}, \boldsymbol{\mu}, \boldsymbol{\Sigma}\right)}}_{\text{KL divergence}}$$
- E-step: 根据贝叶斯法则,令$q_t\left(c_{i}=k\right)=p\left(c_{i}=k | \vec{x}_{i}, \vec{\pi}^{(t)}, \mu^{(t)}, \Sigma^{(t)}\right)\propto p\left(c_{i}=k | \vec{\pi}^{(t)}\right) p\left(\vec{x}_{i} | c_{i}=k, \boldsymbol{\mu}^{(t)}, \boldsymbol{\Sigma}^{(t)}\right)$,容易看出$$q_t\left(c_{i}=k\right)=\frac{\pi_{k}^{(t)} N\left(\vec{x}_{i} | \vec{\mu}_{k}^{(t)}, \Sigma_{k}^{(t)}\right)}{\sum_{j} \pi_{j}^{(t)} N\left(\vec{x}_{i} | \vec{\mu}_{j}^{(t)}, \Sigma_{j}^{(t)}\right)}$$
- M-step: $$\arg\max_{\vec{\pi}, \boldsymbol{\mu}, \boldsymbol{\Sigma}}\sum_{i=1}^{n} \sum_{k=1}^{K} q_t\left(c_{i}=k\right)\ln p\left(\vec{x}_{i}, c_{i}=k | \vec{\pi}, \boldsymbol{\mu}, \boldsymbol{\Sigma}\right)=\arg\max_{\vec{\pi}, \boldsymbol{\mu}, \boldsymbol{\Sigma}}\sum_{i=1}^{n} \sum_{k=1}^{K} q_t\left(c_{i}=k\right)\left[\ln \pi_k+\ln N\left(\vec{x}_{i} | \vec{\mu}_{k}, \Sigma_{k}\right)\right]$$可以得出$\pi_{k}^{(t+1)}=\frac{\sum_{i=1}^{n}q_t\left(c_i=k\right)}{\sum_{j=1}^{K}\sum_{i=1}^{n}q_t\left(c_i=j\right)}, \quad\vec{\mu}_{k}^{(t+1)}=\frac{\sum_{i=1}^{n} q_t\left(c_i=k\right) \vec{x}_{i}}{\sum_{i=1}^{n}q_t\left(c_i=k\right)}, \quad \Sigma_{k}^{(t+1)}=\frac{ \sum_{i=1}^{n} q_t\left(c_i=k\right)\left(\vec{x_{i}}-\vec{\mu}_{k}^{(t+1)}\right)\left(\vec{x}_{i}-\vec{\mu}_{k}^{(t+1)}\right)^{T}}{\sum_{i=1}^{n}q_t\left(c_i=k\right)}$