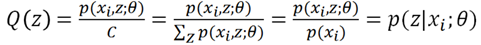
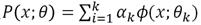
由k个高斯模型加权组成,α是各高斯分布的权重,Θ是参数。对GMM模型的参数估计,就要用EM算法。更一般的讲,EM算法适用于带有隐变量的概率模型的估计,即不同的高斯分布所对应的类别变量。
为何不能使用极大似然估计,如果直接使用极大似然估计,没有考虑数据中的隐变量,很明显是不合适的。
那我们将隐变量考虑进去,最大化似然函数:
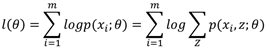
对这个似然函数通过求导的方式明显是很困难的,我们的策略是建立l(θ)的下界,并且求该下界的最大值,重复这个过程,知道收敛到局部最大值。
我们引入一个Q(z),即隐变量z的分布函数
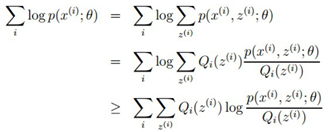
上述不等式成立的条件是使用了Jensen不等式,log是凹函数,满足E(f(x))<= f(E(x)),当且仅当X是常数时,等式成立。
接下来我们我们直接优化最后那个等式是否就可以了呢?答案是不行的,我们必须保证下界是紧的,即等号成立。等式成立的条件是随机变量是常数,也就是
又因为Q(z)是z的分布函数,所以:
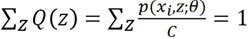
可以求出C值的表达式:代入前面第二个式子,得到:

得到Q(z)之后,我们可以将Q(z)代入含θ的似然函数,求出似然函数的下界(即最大化似然函数),如此反复迭代计算,便可以得到似然函数的局部极大值,那么似然函数最大值对应的θ值就是我们要估计的参数值了。
EM算法:
首先,初始化参数θ
(1)E-Step:根据参数θ计算每个样本属于zi的概率,即这个身高来自四川或东北的概率,这个概率就是Q
(2)M-Step:根据计算得到的Q,求出含有θ的似然函数的下界并最大化它,得到新的参数θ
EM算法求解GMM问题
随机挑选10000名志愿者,测量他们的身高,样本中有男性和女性,身高服从高斯分布,分别为N(μ1, σ1), N(μ2, σ2)
假设取各个高斯分布的概率是φ,如何估计μ,σ,φ呢?
μ,σ,φ是EM算法中的θ
E-step
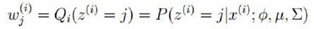
M-step
将Q(z),μ,σ,φ入似然函数,得到:
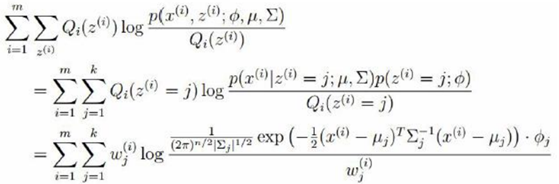
此时,可以使用Jensen不等式,求最紧的下界,反复迭代得到参数值,但是如果直接求导可以得到参数值,无疑是是更加简单的。对于GMM,我们可以直接求导,不需要使用Jensen不等式反复迭代:
对均值求偏导:
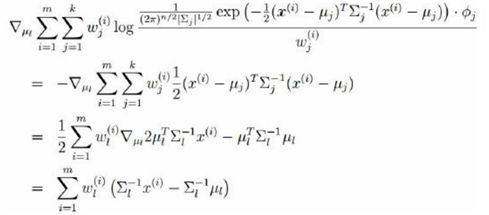
另上式等于0,解得均值为:
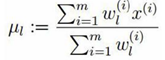
然后对方差求偏导,并使得等式为0,得到方差为:
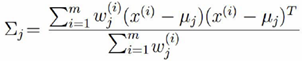
多项分布参数φ的求解:
将似然函数的常数项均删除,得到:
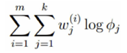
由于多项式分布的概率和为1,建立拉格朗日方程:

对φ求偏导,使等式为0,得到:
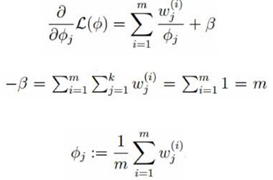
至此,参数μ,σ,φ均已经求出来了