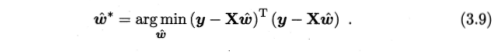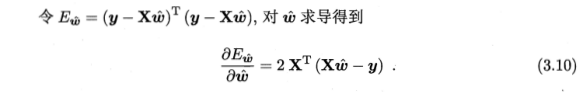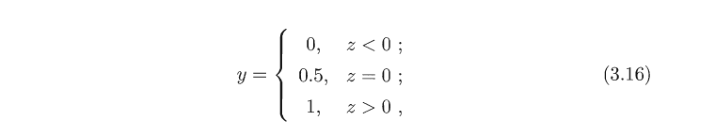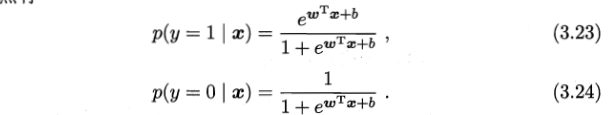西瓜书学习笔记——第三章：线性模型

3.1 基本形式

• 线性模型：试图学得一个通过属性的线性组合来进行预测的函数，即：
  $f\left( x\right) =w_{1}x_{1}+w_{2}x_{2}+\ldots +w_{d}x_{d}+b$
  其中， $x=(x_{1};x_{2};...;x_{d})$是有d个属性的示例
  一般用向量形式写成：
  $f\left( x\right) =w^{T}x+b$

在线性模型的基础上通过引入层级结构或高维映射可得到许多功能更为强大的非线性模型（nonlinear model）。

3.2 线性回归

• 线性回归（linear regression）试图学得一个线性模型以尽可能地预测实值输出标记。

对离散变量的处理

• 若属性值之间存在序关系，可通过连续化将其转换为连续值：如高中低对应{1, 0.5, 0}
• 若属性之间不存在序关系，假定属性值有k个，则通常转化为k维向量：如瓜类的取值黄瓜，西瓜，冬瓜可转化为（0,0,1）,（0,1,0）（1,0,0）

3.2.1 对于样本只有一种属性的情况

线性回归试图学得：
$\qquad\qquad\qquad\qquad\qquad$ $f(x_{i})=wx_{i}+b$，使得 $f(x_{i}) \simeq y_{i}$

对于 $f(x_{i}) \simeq y_{i}$，我们可以通过让均方误差最小化来达到（即找到一条直线，使得所有样本到该直线的欧几里得距离之和最小）。
$\left( w^{\ast },b^{\ast }\right) =arg\space min_{\left( w,b\right) }\sum ^{m}_{i=1}\left( f\left( x_{i}\right) -y_{i}\right) ^{2}$ $\space\space\qquad\qquad =arg\space min_{\left( w,b\right) }\sum ^{m}_{i=1}\left( y_{i}-wx_{i}-b\right) ^{2} \tag{3.4}$

求解 $E\left( w,b\right) = \sum ^{m}_{i=1}\left( y_{i}-wx_{i}-b\right) ^{2}$最小化的过程，称为线性回归模型的最小二乘“参数估计”（parameter estimation）。

$E\left( w,b\right)$是关于 $w$和 $b$的凸函数（U型曲线如f(x)=x^2通常为凸函数，可求其最优解）
对 $E\left( w,b\right)$关于 $w$, $b$求一阶偏导，再令导数为0则可得 $w$, $b$最优解的闭式解：

$\dfrac {\partial E\left( w,b\right) }{\partial w}=2\left( w\sum ^{m}_{i=1}x^{2}_{i}-\sum ^{m}_{i=1}\left( y_{i}-b\right) x_{i}\right)\tag{3.5}$
$\dfrac {\partial E\left( w,b\right) }{\partial b}=2\left(mb-\sum ^{m}_{i=1}\left( y_{i}-wx_{i}\right)\right)\tag{3.6}$

(3.5)，(3.6)公式推导：

待插图......

令(3.5)，(3.6)为零，得 $w$, $b$最优解的闭式解：

$w=\dfrac {\sum ^{m}_{i=1}y_{i}\left( x_{i}-\overline {x}\right) }{\sum ^{m}_{i=1}x^{2}_{i}-\dfrac {1}{m}( \sum ^{m}_{i=1}x_{i})^{2}}\tag{3.7}$

$b=\dfrac {1}{m}\sum ^{m}_{i=1}\left( y_{i}-wx_{i}\right)\tag{3.8}$

其中 $\overline {x}=\dfrac {1}{m}\sum ^{m}_{i=1}x_{i}$为 $x$的均值

公式(3.7)，(3.8)的推导：

待插图......

3.2.2 对于样本由d个属性描述的情况

更一般的情况，样本由多个属性描述。给定数据集 $D=\{(x_{1},y_{1}),(x_{2},y_{2}),...(x_{n},y_{n})\}$，其中 $x_{i}=(x_{i1};x_{i2};...;x_{id})，y_{i} \in\R$

此时线性回归模型试图学得：
$\qquad\qquad\qquad\qquad\qquad$ $f(x_{i})=w^{T}x_{i}+b$，使得 $f(x_{i}) \simeq y_{i}$

此即为多元线性回归（multivariate linear regression）

类似的，我们可以利用最小二乘法来对 $w$和 $b$进行估计。

用矩阵形式表示：

我们把w和b写成向量形式 $\overline {w}=(w,b)$，把数据集 $D$表示成m(d+1)的矩阵 $X$。每一行对应一个示例，该行前d个元素表示d个属性值，最后一个为1（常数项b系数为1）：

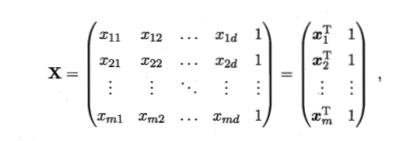
把标记写成向量形式： $y=(y_{1};y_{2};...;y_{3})$，则与公式(3.4)类似的，我们有：

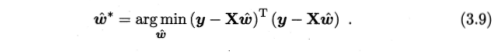
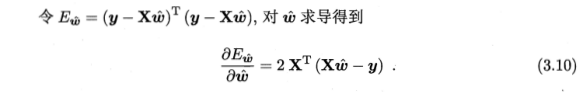
公式(3.10)的推导：

待插图......

令该导数为零可得 $\widehat{w}$最优解的闭式解，但涉及矩阵逆计算，比之前的单变量情形更复杂一些。需进行一下讨论：

①当 $X^{T}X$为满秩矩阵或正定矩阵时：

令式(3.10)为零可得
$\widehat w^{\ast }=\left( X^{T}X\right) ^{-1}X^{T}y\tag{3.11}$

公式(3.11)的推导：

待插图......

令 $\widehat x_{i }=(x_{i};1)$，则最终学得的多元线性回归模型为
$f( \widehat x_{i})= \widehat x_{i}^{T}\left( X^{T}X\right) ^{-1}X^{T}y\tag{3.12}$

公式(3.12)的推导：

待插图......

②当 $X^{T}X$不为满秩矩阵或正定矩阵时：

现实任务中 $X^{T}X$往往不是满秩矩阵。我们会遇到大量变量，其数目超过样例数时， $X$的列数多于行数， $X^{T}X$显然不满秩（线性方程组自变量过多，则会有多组解）。对于解出的多个 $\widehat w$，它们都能使均方误差最小化，选择哪一个作为输出，将由学习算法的归纳偏好决定，常见做法是引入正则化（regularization）项。

3.2.3 广义线性模型（ $y$的衍生）

为了便于讨论，我们把线性回归模型简写为
$y =w^{T}x+b$
若我们认为示例所对应的输出标记是在指数尺度上变化，那就可将输出标记的对数作为线性模型逼近的目标，即
$\ln y=w^{T}x+b$
此即为对数线性回归（log-linear regression），它形式上仍是线性回归，但实质上是求取输入空间到输出空间的非线性函数映射

下图中对数函数起到了将线性回归模型的预测值与真实标记（指数函数的 $y$）联系起来的作用

因此，更一般地，我们可这样推广到一个广义线性模型（generalized linear model）

考虑单调可微函数 $g(\cdot)$（连续且充分光滑），令
$y=g^{-1}(w^{T}x+b)\tag{3.15}$
函数 $g(\cdot)$称为“联系函数”（link function）

显然，对数线性回归就是广义线性模型在 $g(\cdot)=\ln(\cdot)$时的特例

那么，广义线性模型是否也可像式(3.4)(3.9)类似进行均方差误差最小化呢？
当然可以。通常，广义线性模型的参数估计通过加权最小二乘法或极大似然法进行。

<加权最小二乘法链接>

3.3 对数几率回归（用线性模型做分类任务）

线性模型怎么做分类任务？

答案就在式(3.15)的广义模型中：只需找个单调可微函数将分类任务的真实标记 $y$与线性回归模型的预测值 $z$联系起来。
二分类任务的真实标记 $y\in\{0,1\}$，而线性回归模型产生的预测值 $z=w^{T}x+b$为实值，则可将 $z$对应到{0,1}里。最理想的是单位阶跃函数（unit-step function）：

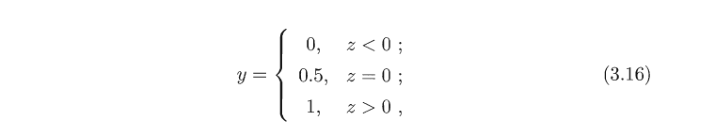
即线性模型的预测值 $z$大于零就判定为正例，小于零就判定为反例，为临界值0时则可任意判定

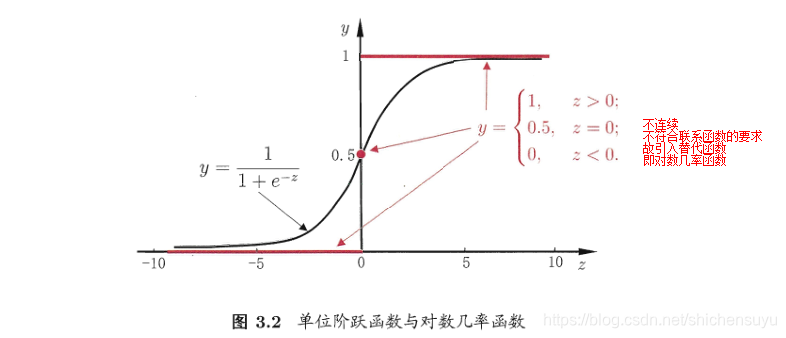
为不连续的单位阶跃函数找到了对数几率函数作为代替函数（可以看到対率函数曲线的特性近似于阶跃函数，它是一种“Sigmoid函数”，它将 $z$值转化为一个接近0或1的 $y$值，其输出值在 $z=0$附近变化很陡）
对数几率函数：
$y=\dfrac {1}{1+e^{-z}}$
将对数几率函数作为 $g^{-}(\cdot)$代入式(3.15)，得到：
$y=\dfrac {1}{1+e^{-\left( w^{T}x+b\right) }} \tag{3.18}$
转化为线性形式则为（类似于式(3.14)）：
$\ln\dfrac {y}{1+y}=w^{T}x+b\tag{3.19}$
若将 $y$看做样本 $x$作为正例的可能性，则 $1-y$是其反例的可能性，两者的比值 $\dfrac{y}{1-y}$称为 “几率”， 反映了 $x$作为正例的 相对可能性，
$\ln\dfrac {y}{1-y}$则为对数几率(log odds，亦称logit)

由式(3.19)可见，式(3.18)实际上是在用线性回归模型的预测结果去逼近真实标记的对数几率

对数几率回归的小总结

求解对数几率回归模型的 $w$和 $b$

首先，我们将式(3.18)中的 $y$视为类后验概率估计 $p(y=1|x)$，则 $1-y$即为 $p(y=0|x)$
则式(3.19)可重写为
$\ln \dfrac {p (y=1|x) }{p( y= 0|x)} =w^{T}x+b\tag{3.22}$
注： $p (y=1|x)+p( y= 0|x)=1$
则有：

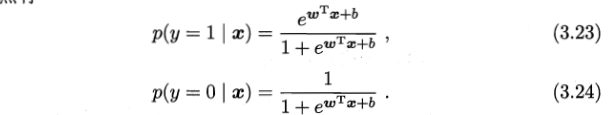
这里我们用极大似然法来估计 $w$和 $b$
给定数据集 $\left\{ \left( x_{i},y_{i}\right) \right\} ^{m}_{i=1}$，对率回归模型最大化“对数似然”（log-likelihood）
$f\left( w,b\right) =\sum ^{m}_{i=1}\ln p\left(y_{i}\right| x_{i};w,b)\tag{3.25}$
注：这里的似然项的参数 $\theta _{c}=(x_{i};w,b)吗？是(w,b)还是(w;b)?$

式(3.26)的推导：

待插入图

由式(3.23)(3.24)(3.25)(3.26)可知，最大化式(3.25)等价于最小化
$l\left( \beta \right) =\sum ^{m}_{i=1}\left( -y_{i}\beta ^{T}\widehat x_{i}+\ln \left( 1+e^{\beta ^{T }\widehat x_{i}}\right) \right)\tag{3.27}$

这是关于 $\beta$的高阶可导连续函数，根据凸优化定理，经典的数值优化算法如梯度下降法，牛顿法都可求其最优解，于是得到
$\beta\ast=arg\space min\space l(\beta)\tag{3.28}$
注：<牛顿法补充链接>

公式推导待插图

笔记已做好，待补充

3.4 线性类别分析（LDA，做分类任务）

3.4.1 LDA的思想

3.4.2 均值向量，协方差，协方差矩阵的概念

3.4.3 LDA二分类的情况

3.4.4 LDA多分类的情况

3.5 多分类学习

3.5.1 多分类学习的基本思路

3.5.2 多分类学习的拆分策略

一对一(OvO)

一对其余(OvR)

多对多(MvM)

最常用的MvM技术：纠错输出码(ECOC)

3.6 类别不平衡问题