最大化期望算法（EM）详解

我们知道最大似然估计的根本目的是根据抽样的到的样本（即数据），反推出最有可能的分布参数（即模型），这是一个非常典型的机器学习的思想。所以在很多领域最大似然估计有着极为广泛的应用。然而，如果已知的数据中含有某些无法观测的隐藏变量时，直接使用最大似然估计是不足以解决问题的。这个时候就要依靠最大化期望（EM）算法了。

简单的说，EM算法是在依赖于无法观测的隐藏变量的概率模型中，寻找参数最大似然估计或者最大后验估计的算法。

1. 最大似然估计

最大似然其实基本的原理非常简单，假设我们手里现在有一个样本，这个样本服从某种分布，而分布有参数，可如果我现在不知道这个样本分布的具体参数是多少，我们就想要通过抽样得到的样本进行分析，从而估计出一个较准确的相关参数。

以上，这种通过抽样结果反推分布参数的方法就是“最大似然估计”。现在简单思考一下怎么去估计：已知的一个抽样结果和可能的分布（比如说高斯分布），那我就像小学生解方程那样呗，先设出分布的参数（比如高斯分布中就是设出 $\sigma$ 和 $\mu$ ），然后我计算得到现在这个抽样数据的概率函数，令这个概率最大，看此时相关参数的取值。

这个思路很容易理解，能使得概率最大的参数一定是“最可能”的那个，这里的“最可能”也就是最大似然估计中“最大似然”的真正含义。

只是这么说可能有点抽象，看一个具体的例子。设产品有合格、不合格两类，未知的是不合格品的概率 $p$ ，显然这是一个典型的两点分布 $b(1, p)$ 。我们用随机变量 $X$ 表示是否合格， $X = 0$ 表示合格， $X = 1$ 表示不合格。如果现在得到了一组抽样数据 $(x_1, x_2, \dots, x_n)$ ，那么不难写出抽样得到这组数据的概率：

\begin{matrix} (1) & f (X_{1} = x_{1}, X_{2} = x_{2}, \dots, X_{n} = x_{n}; p) = \prod_{i = 1}^{n} p^{x_{i}} (1 - p)^{1 - x_{i}} \end{matrix}

$\begin{equation} f(X_1 = x_1, X_2 = x_2, \dots, X_n = x_n; p) = \prod_{i = 1}^n p^{x_i}(1 - p)^{1 - x_i} \end{equation}$

我们把上面这个联合概率叫做样本的似然函数，一般把它两侧同时取对数（记为对数似然函数 $L(\theta)$ ）。 $L(\theta)$ 关于 $p$ 的求偏导数，令偏导数为0，即可求得使得 $L(p)$ 最大的 $p$ 值。

\begin{matrix} (2) & \frac{\partial L (p)}{\partial p} = 0 \Rightarrow \hat{p} = \sum_{i = 1}^{n} x_{i} / n \end{matrix}

$\begin{equation} \frac{\partial L(p)}{\partial p} = 0 \Rightarrow \hat{p} = \sum_{i = 1}^{n} x_i / n \end{equation}$
其中，求得的

p

$p$ 值称为

p

$p$ 的最大似然估计，为示区分，用

\hat{p}

$\hat{p}$ 表示。

其他分布可能计算过程更加复杂，然而基本的步骤与这个例子是一致的。我们总结一下：设总体的概率函数为 $p(x; \theta)$ ， $\theta$ 为一个未知的参数，现已知来自总体的一个样本 $x_1, x_2, \dots, x_n$ 那么求取 $\theta$ 的最大似然估计的步骤如下：

写出似然函数 $L(\theta)$ ，它实际上就是样本的联合概率函数

$\begin{matrix} (3) & L (θ) = p (x_{1}; θ) \cdot p (x_{2}; θ) \cdot \dots p (x_{n}; θ) \end{matrix}$ $\begin{equation} L(\theta) = p(x_1; \theta) \cdot p(x_2; \theta) \cdot \dots p(x_n; \theta) \end{equation}$
对似然函数求取对数，并整理

$\begin{matrix} (4) & \ln (L (θ)) = \ln p (x_{1}; θ) + \dots + \ln p (x_{n}; θ) \end{matrix}$ $\begin{equation} \ln(L(\theta)) = \ln p(x_1; \theta) + \dots + \ln p(x_n; \theta) \end{equation}$
关于参数 $\theta$ 求偏导，并令偏导数为0，解得参数 $\hat{\theta}$ ，这就是参数 $\theta$ 的最大似然估计

$\begin{matrix} (5) & \frac{\partial L (θ)}{\partial θ} = 0 \Rightarrow \hat{θ} = \dots \end{matrix}$ $\begin{equation} \frac{\partial L(\theta)}{\partial \theta} = 0 \Rightarrow \hat{\theta} = \dots \end{equation}$

2. 隐藏变量

上面介绍了最大似然估计，可上面的做法仅适用于不存在隐藏变量的概率模型。什么是隐藏变量呢，我们看这样一个例子。假设现在班上有男女同学若干，同学们的身高是服从正态分布的，当然了，男生身高分布的参数与女生身高分布的参数是不一样的。现在如果给你一个同学的身高，你很难确定这个同学是男是女。如果这个时候抽取样本，让你做上面的最大似然估计，那么就需要做以下两步操作了：

估计一下样本中的每个同学是男生还是女生；
估计男生和女生的身高分布的参数；

第二步就是上面说的最大似然估计，难点在第一步，你还得先猜测男女才行。用更抽象的语言，可以这样描述：属于多个类别的样本混在了一起，不同类别样本的参数不同，现在的任务是从总体中抽样，再通过抽样数据估计每个类别的分布参数。这个描述就是所谓的“在依赖于无法观测的隐藏变量的概率模型中，寻找参数最大似然估计”，隐藏变量在此处就是样本的类别（比如上例中的男女）。这个时候EM算法就派上用场了。

3. EM算法的基本思想

直观考虑这种隐藏变量的问题，你会发现它很麻烦，因为它使得人们陷入了一种两难的境地：我只有知道了哪些样本是属于同一个类别的，才能根据最大似然函数估计这个类别样本的分布参数；同样，我只有知道了不同类别样本的分布参数，才有可能判断现某个样本到底属于哪个类别的可能性更大。

也就是说，你不确定，我就确定不了；而我不确定，你也确定不了。那怎么办？我们可以先让其中一方随便确定一个值，然后用根据这个值看看对方如何变化，再根据对方的变化调整己方，这样你根据我调整，我再根据你调整，循环往复，最终双方都几乎不变了（也就是收敛了），那就可以确定相关的值了。百度百科上有一个形象的例子，我抄过来，大家可以理解一下：

“比如说食堂的大师傅炒了一份菜，要等分成两份给两个人吃，显然没有必要拿来天平一点的精确的去称分量，最简单的办法是先随意的把菜分到两个碗中，然后观察是否一样多，把比较多的那一份取出一点放到另一个碗中，这个过程一直迭代地执行下去，直到大家看不出两个碗所容纳的菜有什么分量上的不同为止。”

EM的求解思路就是我上面所描述的这样。（1）我们先根据经验为每个类别（即隐藏变量）赋予一个初始分布，这相当于是假定了分布参数。然后根据分布的参数可以求取每个数据元组的隐藏变量的期望（相当于实施了归类操作）；（2）再根据归类结果计算分布参数（向量）的最大似然值，然后根据这个最大似然值在反过来重新计算每个元组的隐藏变量的期望。这样循环往复，最终如果隐藏变量的期望与参数的最大似然值趋于稳定了，EM算法就算是执行完毕了。

这么说可能有点抽象，我那上面那个男女生身高的例子再说一遍：（1）首先，我们根据经验，估计男生的身高分布为 $(1.7, 0.1)$ ，女生的为 $(1.55, 0.1)$ ，当然这就是瞎猜的，不一定准。然后你就可以根据参数可以求出每个数据（身高值）应该是男生的还是女生的，这个分类结果就是隐藏变量的期望；（2）这时，写出最大似然函数，根据“已知”的每个数据的隐藏变量求出参数列表的最大似然值，反过来再执行（1）步，反复迭代，直到收敛。

综上，我们也就能理解为什么EM算法要叫“最大化期望”算法了，它是由两步组成，第一步是E步，就是求期望；第二步是M步，就是最大化：

E步(Expectation)：根据当前的参数值，计算样本隐藏变量的期望；
M步(Maximum)：根据当前样本的隐藏变量，求解参数的最大似然估计；

4. EM算法的具体步骤

现有样本 $x_1, x_2, \dots, x_n$ ，设每个样本的隐藏变量（这里就当做是属于的类别）为 $z_i$ ，其取值有 $m$ 种： $z^{(1)}, \dots, z^{(m)}$ 。EM算法的任务是求解不同类别样本的参数的最大似然估计。具体步骤如下：

4.1 写出对数化后的似然函数

假设对数似然函数如下：

\begin{matrix} (1) & \begin{aligned} \ln L (θ) & = \ln (p (x_{1}; θ) \cdot p (x_{2}; θ) \cdot \dots \cdot p (x_{n}; θ)) \\ = \sum_{i = 1}^{n} \ln p (x_{i}; θ) \\ = \sum_{i = 1}^{n} \ln \sum_{j = 1}^{m} p (x_{i}, z^{(j)}; θ) \end{aligned} \end{matrix}

$\begin{equation} \begin{aligned} \ln L(\theta) &= \ln(p(x_1; \theta) \cdot p(x_2; \theta) \cdot \dots \cdot p(x_n; \theta))\\ &= \sum_{i = 1}^n \ln p(x_i; \theta)\\ &= \sum_{i = 1}^n \ln \sum_{j = 1}^mp(x_i, z^{(j)}; \theta)\\ \end{aligned} \end{equation}\tag{1}$

公式(1)其实是两步，第一步是对似然函数正常的对数化处理，第二步则把每个 $p(x_i; \theta)$ 用不同类别的联合分布的概率和表示。可以理解为抽到样本 $x_i$ 的概率为 $x_i$ 属于类 $z^{(1)}$ 的概率，加上 $x_i$ 属于类 $z^{(2)}$ 的概率，加上。。。一直加到 $x_i$ 属于类 $z^{(m)}$ 的概率。

本质上讲，我们的目的是要求公式(1)的最大值。但是你看，现在(1)中存在对数项里面的加和，如果求导的话，是非常麻烦的，所以，我们首先想到的就是对公式(1)化简，转换其形式。

为了方便推导，我们将 $x_i$ 对 $z$ 的分布函数用 $Q_i(z)$ 表示。那么对于 $Q_i(z)$ ，它一定满足如下条件：

\begin{matrix} (6) & \sum_{j = 1}^{m} Q_{i} (z^{(j)}) = 1, Q_{i} (z^{(j)}) \geq 0 \end{matrix}

$\begin{equation} \sum_{j = 1}^m Q_i(z^{(j)}) = 1,~~ Q_i(z^{(j)}) \geq 0 \end{equation}$

所以公式(1)可以这样化简：

\begin{matrix} (2) & \begin{aligned} \ln L (θ) & = \sum_{i = 1}^{n} \ln \sum_{z} p (x_{i}, z^{(j)}; θ) \\ = \sum_{i = 1}^{n} \ln \sum_{j = 1}^{m} Q_{i} (z^{(j)}) \frac{p (x_{i}, z^{(j)}; θ)}{Q_{i} (z^{(j)})} \\ \geq \sum_{i = 1}^{n} \sum_{j = 1}^{m} Q_{i} (z^{(j)}) \ln \frac{p (x_{i}, z^{(j)}; θ)}{Q_{i} (z^{(j)})} \end{aligned} \end{matrix}

$\begin{equation} \begin{aligned} \ln L(\theta) &= \sum_{i = 1}^n \ln \sum_{z}p(x_i, z^{(j)}; \theta)\\ &= \sum_{i = 1}^n \ln \sum_{j = 1}^m Q_i(z^{(j)}) \frac{p(x_i, z^{(j)}; \theta)}{Q_i(z^{(j)})}\\ &\geq \sum_{i = 1}^n \sum_{j = 1}^m Q_i(z^{(j)}) \ln \frac{p(x_i, z^{(j)}; \theta)}{Q_i(z^{(j)})} \end{aligned} \end{equation}\tag{2}$

这里的公式(2)非常重要，几乎可以说是整个EM算法的核心公式。可以看到，化简的过程实际上包含了两步，第一是简单的把 $Q_i(z)$ 嵌入，第二则是根据 $\ln()$ 函数是凸函数的性质得到的最后那个 $\geq$ 的结果。关于凸函数，我会在本文4.2节中详细说。先看看这个式子，我们发现，通过化简，其实是求得了似然函数的一个下界（记为 $J(z, Q)$ ）：

\begin{matrix} (7) & J (z, Q) = \sum_{i = 1}^{n} \sum_{j = 1}^{m} Q_{i} (z^{(j)}) \ln \frac{p (x_{i}, z^{(j)}; θ)}{Q_{i} (z^{(j)})} \end{matrix}

$\begin{equation} J(z, Q) = \sum_{i = 1}^n \sum_{j = 1}^m Q_i(z^{(j)}) \ln \frac{p(x_i, z^{(j)}; \theta)}{Q_i(z^{(j)})} \end{equation}$

这个 $J(z, Q)$ 其实就是变量 $\frac{p(x_i, z^{(j)}; \theta)}{Q_i(z^{(j)})}$ 的期望。回忆一下期望的算法是 $E(X) = \sum xp(x)$ ，这里 $Q_i(z^{(j)})$ 相当于是概率。

我们发现， $J(z, Q)$ 是比较容易求导的（因为是一个简单的加法式子），但现在的问题在于对下界求导没用，我们要对似然函数求导才行。换个思路想想，下界取决于 $p(x_i, z^{(j)}; \theta)$ 和 $Q_i(z^{(j)})$ ，我们如果能通过这两个值不断提升下界，使之不断逼近似然函数 $ln~L(\theta)$ ，在某种情况下，如果 $J(z, Q) = ln~ L(\theta)$ ，那就大功告成了。说到这，先暂停，我们看一下凸函数的定义和性质。

4.2 凸函数与Jensen不等式

4.2.1 凸函数

定义1-凸函数：设函数 $f(x)$ 在定义域 $D$ 上式凸函数，当且仅当 $f(x)$ 对 $D$ 任意两点 $x_1$ , $x_2$ 满足：

\begin{matrix} (8) & f (λ x_{1} + (1 - λ) x_{2}) \leq λ f (x_{1}) + (1 - λ) f (x_{2}) \end{matrix}

$\begin{equation} f(\lambda x_1 + (1 - \lambda)x_2) \leq \lambda f(x_1) + (1 - \lambda) f(x_2) \end{equation}$
则我们将这样的函数称为“凸函数”。其中，

λ \in (0, 1)

$\lambda \in (0, 1)$ 。

定义2-严格凸函数：如果将定义1中不等式的” $\leq$ ”换成” $<$ ”，则这样的凸函数为严格凸函数。

注：有的教材中对凸函数的定义与上面我给出的是相反的，认为 $f(\lambda x_1 + (1 - \lambda)x_2) \geq \lambda f(x_1) + (1 - \lambda) f(x_2)$ 的函数才叫凸函数，而把上面那个定义的函数叫做“凹函数”。其实就数据挖掘和机器学习领域的学习来看，怎么定义都无所谓，所谓“凸”，你从另一个角度看，它就是“凹”的，而且不论怎么定义，两个函数的一些重要的性质是一样的。这里，我们默认上面的定义1。

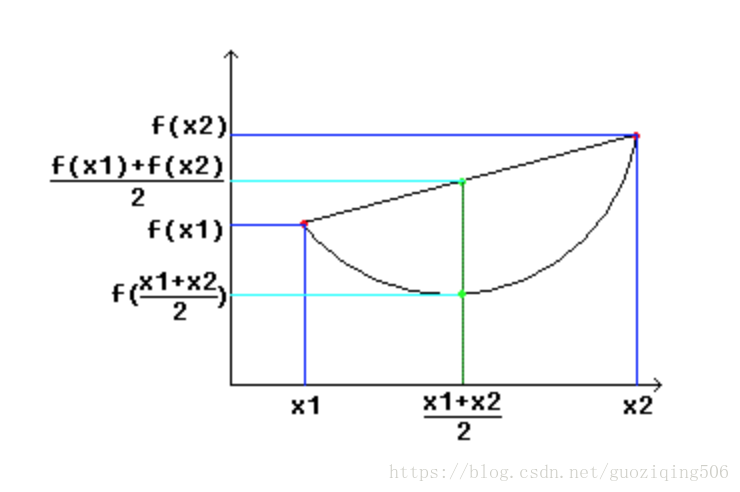
另外，一般用下图直观感受凸函数，图中取 $\lambda = 1/2$ ，显然这图像是向下“凸”的：

注：图像截取自博客：【机器学习理论】第4部分凸函数）

定义3-凸函数的一般化定义：若 $f(x)$ 为凸函数， $x_1, x_2, \dots, x_n$ 是定义域 $D$ 内的 $n$ 个值，那么：

\begin{matrix} (9) & f (λ_{1} x_{1} + λ_{1} x_{1} + \dots + λ_{n} x_{n}) \leq λ_{1} f (x_{1}) + λ_{2} f (x_{2}) + \dots + λ_{n} f (x_{n}) \end{matrix}

$\begin{equation} f(\lambda_1 x_1 + \lambda_1 x_1 + \dots + \lambda_n x_n) \leq \lambda_1 f(x_1) + \lambda_2 f(x_2) + \dots + \lambda_n f(x_n) \end{equation}$
其中，

λ_{i} \in (0, 1)

$\lambda_i \in (0, 1)$ ，且

\sum_{i = 1}^{n} λ_{i} = 1

$\sum_{i = 1}^n \lambda_i = 1$ 。这也就是公式(2)中得到似然函数下界的依据。

4.2.2 凸函数的性质

下面给出凸函数的两个重要性质：

若 $f(x)$ 在 $D$ 上连续，且在 $D$ 上二阶可导，则若 $f''(x) > 0$ ， $f(x)$ 为凸函数；反之， $f(x)$ 为凹函数
Jensen不等式：若 $f(x)$ 是凸函数，则下面的公式(3)成立：

\begin{matrix} (3) & f ((x_{1} + x_{2} + \dots + x_{n}) / n) \leq \frac{1}{n} (f (x_{1}) + f (x_{2}) + \dots + f (x_{n})) \end{matrix}

$\begin{equation} f((x_1 + x_2 + \dots + x_n) / n) \leq \frac{1}{n} (f(x_1) + f(x_2) + \dots + f(x_n)) \end{equation}\tag{3}$

可以看出，Jensen不等式就是凸函数的一般化定义的公式的一种特例（参数 $\lambda_i$ 全部取等了）。

放到概率论中，Jensen不等式是如下表述的。若 $f(x)$ 为凸函数，则：

\begin{matrix} (4) & f (E (X)) \geq E (f (x)) \end{matrix}

$\begin{equation} f(E(X)) \geq E(f(x)) \end{equation}\tag{4}$

公式(4)与公式(3)是一样的，只是在概率论中，把系数 $\lambda_i$ 的概念用概率替换了。需要注意的是，如果 $f(x)$ 为严格凸函数，那么当且仅当变量 $X$ 为常数时，即 $X = E(X)$ 时，公式(4)的等号才成立。

4.3 E步求取隐藏变量的期望

了解了公式(4)，即Jensen不等式中等式成立的条件。我们回过头再看4.1节末尾的问题。此时使得 $\ln L(\theta) = J(z, Q)$ 的条件就很明显了，因为 $J(z, Q)$ 是变量 $\frac{p(x_i, z^{(j)}; \theta)}{Q_i(z^{(j)})}$ 的期望（相当于 $E(f(x))$ ），那根据Jensen不等式， $X$ 为常数时，等号成立。

我们不妨设：

\begin{matrix} (10) & \frac{p (x_{i}, z^{(j)}; θ)}{Q_{i} (z^{(j)})} = c \end{matrix}

$\begin{equation} \frac{p(x_i, z^{(j)}; \theta)}{Q_i(z^{(j)})} = c \end{equation}$

其中c为常数。因为 $\sum_{j = 1}^m Q_i(z^{(j)}) = 1$ ，所以 $\sum_{z} p(x_i, z^{(j)}; \theta) = c$ ，有下式成立：

\begin{matrix} (5) & \begin{aligned} Q_{i} (z^{(j)}) & = \frac{p (x_{i}, z^{(j)}; θ)}{\sum_{j = 1}^{m} p (x_{i}, z^{(j)}; θ)} \\ = \frac{p (x_{i}, z^{(j)}; θ)}{p (x_{i}; θ)} \\ = p (z^{(j)} | x_{i}; θ) \end{aligned} \end{matrix}

$\begin{equation} \begin{aligned} Q_i(z^{(j)}) &= \frac{p(x_i, z^{(j)}; \theta)}{\sum_{j = 1}^m p(x_i, z^{(j)}; \theta)}\\ &= \frac{p(x_i, z^{(j)}; \theta)}{p(x_i; \theta)}\\ &= p(z^{(j)}|x_i; \theta) \end{aligned} \end{equation}\tag{5}$

其中 $p(z^{(j)}|x_i; \theta)$ 是为 $z_i$ 的后验概率。公式(5)解决了如何选择 $Q(z)$ 能使得似然函数与其下界相等的问题，其实就是令 $Q_i(z^{(j)})$ 为 $z^{(j)}$ 的后验概率即可。实际操作中，这个后验概率是根据初始的分布参数决定的。这一步就是EM算法中的E步， $Q_i(z^{(j)})$ 就是隐藏变量的期望。

4.4 M步求解最大似然函数

跟4.1节介绍的方法一致，现在既然

\begin{matrix} (11) & \ln L (θ) = \sum_{i = 1}^{n} \sum_{j = 1}^{m} Q_{i} (z^{(j)}) \ln \frac{p (x_{i}, z^{(j)}; θ)}{Q_{i} (z^{(j)})} \end{matrix}

$\begin{equation} \ln L(\theta) = \sum_{i = 1}^n \sum_{j = 1}^m Q_i(z^{(j)}) \ln \frac{p(x_i, z^{(j)}; \theta)}{Q_i(z^{(j)})} \end{equation}$

那就对这个函数关于 $\theta$ 求偏导，令偏导数为0即可。然后迭代执行E步和M步，直到收敛。

EM算法的E步和M步可以形式化的表示如下：

E步： $Q_i(z^{(j)}) = p(x_i, z^{(j)}; \theta)$
M步： $\theta = max_{\theta} \sum_{i = 1}^n \sum_{j = 1}^m Q_i(z^{(j)}) \ln \frac{p(x_i, z^{(j)}; \theta)}{Q_i(z^{(j)})}$

5. EM算法的收敛性证明

但是我们写到这里还有一个疑问，这种反复迭代一定会收敛吗？假定 $\theta^{(t)}$ 和 $\theta^{(t + 1)}$ 为第 $t$ 轮和第 $t + 1$ 轮迭代后的结果， $l(\theta^{(t)})$ 和 $l(\theta^{(t + 1)})$ 为对应的似然函数。显然，如果 $l(\theta^{(t)}) \leq l(\theta^{(t + 1)})$ ，那么随着迭代次数的增加，最终会一步步逼近最大似然值。也就是说，只需要证明公式(6)成立即可。

\begin{matrix} (6) & l (θ^{(t)}) < l (θ^{(t + 1)}) \end{matrix}

$\begin{equation} l(\theta^{(t)}) < l(\theta^{(t + 1)}) \end{equation}\tag{6}$

证明：得到 $\theta^{(t)}$ 后，执行E步：

\begin{matrix} (20) & Q_{i}^{t} (z^{(j)}) = p (z^{(j)} | x_{i}; θ^{t}) \end{matrix}

$\begin{equation} Q_i^{t}(z^{(j)}) = p(z^{(j)}|x_i; \theta^{t}) \end{equation}$

此时，

\begin{matrix} (22) & l (θ^{(t)}) = \sum_{i = 1}^{n} \sum_{j = 1}^{m} Q_{i} (z^{(j)}) \ln \frac{p (x_{i}, z^{(j)}; θ^{t}))}{Q_{i} (z^{(j)})} \end{matrix}

$\begin{equation} l(\theta^{(t)}) =\sum_{i = 1}^n \sum_{j = 1}^m Q_i(z^{(j)}) \ln \frac{p(x_i, z^{(j)}; \theta^{t}))}{Q_i(z^{(j)})} \end{equation}$

然后执行M步，求偏导为0，得到 $\theta^{(t + 1)}$ ，此时有公式(7)成立：

\begin{matrix} (7) & \begin{aligned} l (θ^{(t + 1)}) & \geq \sum_{i = 1}^{n} \sum_{j = 1}^{m} Q_{i} (z^{(j)}) \ln \frac{p (x_{i}, z^{(j)}; θ^{(t + 1)}))}{Q_{i} (z^{(j)})} \\ \geq \sum_{i = 1}^{n} \sum_{j = 1}^{m} Q_{i} (z^{(j)}) \ln \frac{p (x_{i}, z^{(j)}; θ^{t}))}{Q_{i} (z^{(j)})} = l (θ^{t}) \end{aligned} \end{matrix}

$\begin{equation} \begin{aligned} l(\theta^{(t + 1)}) &\geq \sum_{i = 1}^n \sum_{j = 1}^m Q_i(z^{(j)}) \ln \frac{p(x_i, z^{(j)}; \theta^{(t + 1)}))}{Q_i(z^{(j)})}\\ & \geq \sum_{i = 1}^n \sum_{j = 1}^m Q_i(z^{(j)}) \ln \frac{p(x_i, z^{(j)}; \theta^{t}))}{Q_i(z^{(j)})} = l(\theta^{t}) \end{aligned} \end{equation}\tag{7}$

简单说一下公式(7)，第一步 $l(\theta^{(t + 1)}) \geq \sum_{i = 1}^n \sum_{j = 1}^m Q_i(z^{(j)}) \ln \frac{p(x_i, z^{(j)}; \theta^{(t + 1)})}{Q_i(z^{(j)})}$ 是由前面的公式(2)决定的；

第二步 $\geq \sum_{i = 1}^n \sum_{j = 1}^m Q_i(z^{(j)}) \ln \frac{p(x_i, z^{(j)}; \theta^{t}))}{Q_i(z^{(j)})}$ 是M步的定义，M步中，将 $\theta^{t}$ 调整到 $\theta^{(t + 1)}$ 就是为了使似然函数 $l(\theta^{(t + 1)})$ 最大化。

综上，我们证明了EM算法的收敛性。