Problem A BBQ Easy
简要题意:给定 \(2n\) 个数字,两两配对,一对的贡献为它们的 \(min\) ,求最大贡献和。\(n\le 100\)
tag:小学生贪心
题解:排个序,求奇数位之和,证明显然。
#include <cstdio>
using namespace std;
const int N=105;
int a[N];
int main (){
int n,ans=0;
scanf ("%d",&n);
for (int i=1;i<=(n<<1);i++) scanf ("%d",&a[i]);
sort(a+1,a+(n<<1)+1);
for (int i=1;i<=n;i++) ans+=a[(i-1)<<1|1];
printf ("%d",ans);
return 0;
}Problem B Mysterious Light
简要题意:给一个边长为 \(n\) 的等边三角形,从一个线段 \(ab\) 上的点 \(x\) 发射激光,边缘是镜子,遇到会被反射,遇到自己的轨迹也会被反射,回到原点被吸收,(下图是一个例子)问路径总长. \(n\le 10^{12}\)
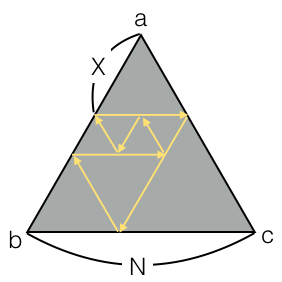
tag:模拟,递归
题解:每次要做的事情就是将一个平行四边形切成边长为短边长度的若干等边三角形,直到切不出来位置,切不出来的时候,就出现了一个新的平行四边形,递归即可。
#include <cstdio>
#define ll long long
ll n,x;
inline ll work(ll l1,ll l2){
if (!l2) return -l1;
return work(l2,l1%l2)+2*(l1/l2)*l2;
}
int main() {
scanf("%lld%lld",&n,&x);
printf("%lld\n",work(x,n-x)+n);
return 0;
}Problem C Shorten Diameter
简要题意:给你一棵 \(n\) 个节点的树,你可以删除叶子,问最少删除多少点之后可以使它的直径小于等于 \(k\) \(n\le 1000\)
tag:图论,贪心
题解:根据 \(k\) 的奇偶性分类做,如果是偶数,枚举一个点作为直径中点,把距离这个点大于 \(\frac{k}{2}\)的点全部砍掉,如果是奇数,枚举一条边, 把距离这条边大于 \(\frac{k-1}{2}\) 的点砍掉,然后取 \(min\) 即可
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N=2005;
int Head[N],Next[N<<1],Adj[N<<1],tot=0,dis[N];
int u[N],v[N];
inline void addedge(int u,int v){
Next[++tot]=Head[u];
Head[u]=tot;
Adj[tot]=v;
Next[++tot]=Head[v];
Head[v]=tot;
Adj[tot]=u;
}
inline void dfs(int x,int f){
for (int e=Head[x];e;e=Next[e])
if (Adj[e]!=f) dis[Adj[e]]=dis[x]+1,dfs(Adj[e],x);
}
int main (){
int n,k;
scanf ("%d%d",&n,&k);
for (int i=1;i<n;i++){
scanf ("%d%d",&u[i],&v[i]);
addedge(u[i],v[i]);
}
int ans=n;
if (k&1){
for (int i=1;i<n;i++){
dis[u[i]]=dis[v[i]]=0;dfs(u[i],v[i]),dfs(v[i],u[i]);
int cnt=0;
for (int j=1;j<=n;j++) if (dis[j]>(k/2)) cnt++;
ans=min(ans,cnt);
}
}else{
for (int i=1;i<=n;i++){
dis[i]=0;int cnt=0;dfs(i,0);
for (int j=1;j<=n;j++) if (dis[j]>(k/2)) cnt++;
ans=min(ans,cnt);
}
}
printf ("%d",ans);
return 0;
}
Problem D Arrays and Palindrome
简要题意:给定你 \(a\) 序列,请你重排它并构造一个 \(b\) 序列,使得两个序列元素和均为 \(n\) 。
对于一个长度为 \(n\) 的字符串,满足如果前 \(a_1\) 个是回文串,接下来 \(a_2\) 个是回文串……且前 \(b_1\) 个是回文串,接下来 \(b_2\) 个是回文串……那么这个字符串处处相同。
tag:图论,思维,贪心,构造
题解:建立一个图论模型。对于钦定相等的两个点,给它们连一条边,然后一个联通块内的所有点都要相等。那对于一个长度为 \(n\) 的回文串,其实就是钦定了 \(i\) 与 \(n-i+1\) 要相等,相当于在图中连了 \(\frac{n}{2}\) 条边。为了让 \(n\) 个点连通,我们需要至少 \(n-1\) 条边。对于一个由若干段回文构成的序列,它至多连出 \(\frac{n-odd}{2}\) 条边,其中 \(odd\) 表示大小为奇数的段数。可以看出,若一开始给定的数列中,奇数大于 \(2\) 个,必然无解。那么对于一个有解的数列,把奇数放在首尾得到序列 \(1\) ,第一个数减一、最后一个数加一得到序列 \(2\) 。这样,每一段都是错开的,每一条边都必然连接两个原本不连通的块。因为题目要求不能输出 \(0\) ,所以需要再特判一下。
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N=1005;
int a[N];
int main (){
int n,m;scanf ("%d%d",&n,&m);
int t1=m,t2=1;
for (int i=1;i<=m;i++) scanf ("%d",&a[i]);
int cnt=0;
for (int i=1;i<=m;i++)
if (a[i]&1) {
cnt++;
if (cnt==1) t1=i;
if (cnt==2) t2=i;
if (cnt>2){
puts("Impossible");
return 0;
}
}
swap(a[m],a[t1]);
swap(a[1],a[t2]);
if (m==1&&a[1]==1) {puts("1\n1\n1");return 0;}
for (int i=1;i<=m;i++) printf("%d ",a[i]);
if (m==1) {printf("\n2\n%d 1\n",a[1]-1);return 0;}
printf ("\n%d\n%d ",a[m]>1?m:m-1,a[1]+1);
for (int i=2;i<m;i++) printf("%d ",a[i]);
if (a[m]>1) printf("%d\n",a[m]-1);
return 0;
}
Problem E BBQ Hard
简要题意:有 \(n\) 个数对 \((A_i,B_i)\) ,求出 \(\sum_{i=1}^{n}\sum_{j=i+1}^n{A_i+B_i+A_j+B_j \choose A_i+A_j}\) 答案对 \(10^9+7\) 取模 。\(n\le 2\times 10^5,\ A_i,B_i\le 1000\)
tag:组合意义,计数,dp
题解:神仙题,毫无思路 可能因为我太菜了。
考虑这个东西的组合意义,我们知道 \(\binom{x+y}{x}\) 可以表示成坐标轴上 \((0,0)\) 走到 \((x,y)\) ,每次只能向右或上走的方案数,所以问题变成了从 \((0,0)\) 走到 \((A_i+A_j,B_i+B_j)\) 的方案数。
我们平移一下这两个点,变成了从 \((-A_i,-B_i)\) 走到 \((A_j,B_j)\) 的方案数,那么我们换一个思维,把所有的 \((-A_i,-B_i)\) 作为起点,求出所有的 \((A_j,B_j)\) 到它的路径条数。
那么我们考虑递推,对于每一个 \(i\) ,给 \((-A_i,-B_i)\) 的值 \(+1\),然后 \(dp[i][j]=dp[i-1][j]+dp[i][j-1]\)
那么答案就是 \(\frac{\sum_{i=1}^ndp[A_i][B_i]-\binom{2A_i+2B_i}{2A_i}}{2}\),后面那个东西是 \((-A_i,-B_i)\) 到 \((A_i,B_i)\) 的方案数,多算了减掉
时间复杂度 \(O(n+A\times B)\)
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N=2e5+5,M=2005,Mod=1e9+7;
int a[N],b[N];
int dp[M<<1][M<<1],fac[M<<2],inv[M<<2];
#define C(n,m) (1ll*fac[n]*inv[m]%Mod*inv[n-m]%Mod)
#define dp(i,j) dp[i+M][j+M]
inline int qpow(int a,int b){
int ans=1;while (b){if (b&1) ans=1ll*ans*a%Mod;b>>=1,a=1ll*a*a%Mod;}
return ans;
}
inline int mo(int x){return x>=Mod?x-Mod:x;}
int main (){
int n;scanf ("%d",&n);
for (int i=1;i<=n;i++)
scanf ("%d%d",&a[i],&b[i]);
fac[0]=1;for (int i=1;i<=8000;i++) fac[i]=1ll*fac[i-1]*i%Mod;
inv[8000]=qpow(fac[8000],Mod-2);for (int i=7999;i>=0;i--) inv[i]=1ll*inv[i+1]*(i+1)%Mod;
for (int i=1;i<=n;i++) dp(-a[i],-b[i])++;
for (int i=-2000;i<=2000;i++)
for (int j=-2000;j<=2000;j++)
dp(i,j)=mo(dp(i,j)+mo(dp(i-1,j)+dp(i,j-1)));
int ans=0;
for (int i=1;i<=n;i++) ans=((ans+dp(a[i],b[i])-C(2*(a[i]+b[i]),2*a[i]))%Mod+Mod)%Mod;
printf ("%d",1ll*ans*qpow(2,Mod-2)%Mod);
return 0;
}
update on 2019.04.25
如果仅仅满足 \(\sum_{i=1}^n(x_i+y_i)\le 2\times 10^7\) ,也是可以做的
我们观察到第一象限的任何一个点到第三象限必定经过 \(y=-x\) 这条直线,那么我们考虑枚举经过的是哪一个点
时间复杂度 \(O(\sum x_i+y_i)\)
Problem F Wide Swap
简要题意:给定一个元素集合 \(\{1,2....N\}\) 的排列 \(P\) ,当有 \(i,j\) 满足 \(j-i\ge K\) 且 \(|P_i-P_j|=1\) 可以交换 \(P_i,P_j\)
求可能的字典序中最小的排列。\(N\le 5\times 10^5\)
tag:拓扑排序,线段树,贪心,思维
题解:依然毫无思路
首先考虑调换权值与下标的位置,那么就可以把题目转换成:相邻元素且权值差 \(\ge k\) 的可以换顺序,让前面的权值尽量小的序列。
从位置 \(i\) 向后面的 \(j\) 比较,如果满足条件 \(abs(a[i]-a[j])<k\) ,那么 \(i,j\) 的相对位置关系就确定了,可以连边,这样问题就变成了一个明显的拓扑排序。
不过这样连边数是 \(N^2\) 级别的,需要优化。
因为要求前面的权值尽可能小,所以连向的是最小的边,所以从 \(a[i]\) 向 \((a[i]+1,a[i]+k-1)\) 中下标最小的连边就可以了,反过来,也要向 \((a[i]-k+1,a[i]-1)\) 中下标最大的连边,这样可以包含所有情况,因为它们的相对位置一定也靠连边确定了。
这样,我们把边数优化到了 \(O(n)\) 级别,算法时间复杂度 \(O(nlogn)\)
#include <queue>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
priority_queue <int , vector <int >,greater <int > > Q;
const int N=500005;
#define mid ((l+r)>>1)
int a[N],val[N<<2];
inline int query(int root,int l,int r,int L,int R){
if (r<L||l>R) return 0;
if (L<=l&&r<=R) return val[root];
return max(query(root<<1,l,mid,L,R),query((root<<1)|1,mid+1,r,L,R));
}
inline void update(int root,int l,int r,int x,int y){
if (l==r) {val[root]=y;return;}
if (x<=mid) update(root<<1,l,mid,x,y);
else update((root<<1)|1,mid+1,r,x,y);
val[root]=max(val[root<<1],val[(root<<1)|1]);
}
int Head[N],Next[N<<1],Adj[N<<1],tot=0,d[N],ans[N];
inline void addedge(int u,int v){Next[++tot]=Head[u],Head[u]=tot,Adj[tot]=v,d[v]++;}
int main (){
int n,k;scanf ("%d%d",&n,&k);
for (int i=1,x;i<=n;i++) scanf ("%d",&x),a[x]=i;
for (int i=1;i<=n;i++){
int t=query(1,1,n,max(1,a[i]-k+1),a[i]);
if (t) addedge(a[t],a[i]);
t=query(1,1,n,a[i],min(n,a[i]+k-1));
if (t) addedge(a[t],a[i]);
update(1,1,n,a[i],i);
}
for (int i=1;i<=n;i++) if (!d[i]) Q.push(i);
int Time=0;
while (!Q.empty()){
int x=Q.top();ans[x]=++Time;Q.pop();
for (int e=Head[x];e;e=Next[e]){
d[Adj[e]]--;
if (!d[Adj[e]]) Q.push(Adj[e]);
}
}
for (int i=1;i<=n;i++) printf ("%d\n",ans[i]);
return 0;
}