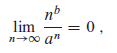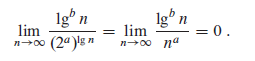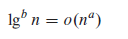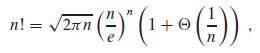笔记参考链接:http://www.cnblogs.com/wuwenyan/p/4982713.html
习题参考链接1:http://www.cnblogs.com/Jiajun/archive/2013/05/06/3063574.html
习题参考链接2:https://ita.skanev.com/
当算法的输入
n
n
n
我们需要关心的是输入规模无限增加,在极限中,运行时间是如何随着输入规模增大而增加的,通常来说,在极限情况下渐进地更优的算法在除很小的输入外的所有情况下将是最好的选择。
前提假设:本章定义的所有用在渐近记号中的函数均渐近非负(包括f(n),g(n))。
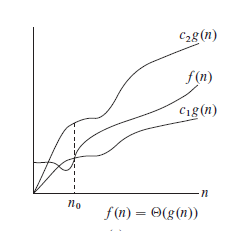
Θ
\Theta
Θ 定义:对于一个给定的函数
g
(
n
)
g(n)
g ( n )
Θ
(
g
(
n
)
)
\Theta(g(n))
Θ ( g ( n ) ) 函数的集合 :
:
存
在
正
常
量
、
和
,
使
得
对
所
有
有
Θ
(
g
(
n
)
)
=
{
f
(
n
)
:
存
在
正
常
量
c
1
、
c
2
和
n
0
,
使
得
对
所
有
n
≥
n
0
,
有
0
≤
c
1
g
(
n
)
≤
f
(
n
)
≤
c
2
g
(
n
)
}
:存在正常量、和,使得对所有有\Theta(g(n))=\{f(n):存在正常量c_1、c_2和n_0,使得对所有n\geq n_0,有0\leq c_1g(n)\leq f(n)\leq c_2g(n)\}
: 存 在 正 常 量 、 和 , 使 得 对 所 有 有 Θ ( g ( n ) ) = { f ( n ) : 存 在 正 常 量 c 1 、 c 2 和 n 0 , 使 得 对 所 有 n ≥ n 0 , 有 0 ≤ c 1 g ( n ) ≤ f ( n ) ≤ c 2 g ( n ) }
含义是:若存在常数
c
1
c_1
c 1
c
2
c_2
c 2
n
n
n
f
(
n
)
f(n)
f ( n )
c
1
g
(
n
)
c_1g(n)
c 1 g ( n )
c
2
g
(
n
)
c2g(n)
c 2 g ( n )
f
(
n
)
f(n)
f ( n )
Θ
(
g
(
n
)
)
\Theta(g(n))
Θ ( g ( n ) )
g
(
n
)
g(n)
g ( n )
f
(
n
)
f(n)
f ( n )
扫描二维码关注公众号,回复:
6152687 查看本文章
注意:
Θ
(
g
(
n
)
)
\Theta(g(n))
Θ ( g ( n ) ) 集合 ,所以如果要表示
f
(
n
)
f(n)
f ( n )
Θ
(
g
(
n
)
)
\Theta(g(n))
Θ ( g ( n ) )
f
(
n
)
∈
Θ
(
g
(
n
)
)
f(n)\in \Theta(g(n))
f ( n ) ∈ Θ ( g ( n ) )
f
(
n
)
=
Θ
(
g
(
n
)
)
f(n)=\Theta(g(n))
f ( n ) = Θ ( g ( n ) )
下图形象地表示了渐近紧确界的形式:
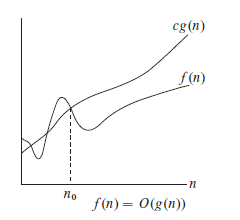
O
O
O 定义:对于一个给定的函数
g
(
n
)
g(n)
g ( n )
O
(
g
(
n
)
)
O(g(n))
O ( g ( n ) ) 函数的集合 :
:
存
在
正
常
量
和
,
使
得
对
所
有
有
O
(
g
(
n
)
)
=
{
f
(
n
)
:
存
在
正
常
量
c
和
n
0
,
使
得
对
所
有
n
≥
n
0
,
有
0
≤
f
(
n
)
≤
c
g
(
n
)
}
:存在正常量和,使得对所有有O(g(n))=\{f(n):存在正常量c和n_0,使得对所有n\geq n_0,有0\leq f(n)\leq cg(n)\}
: 存 在 正 常 量 和 , 使 得 对 所 有 有 O ( g ( n ) ) = { f ( n ) : 存 在 正 常 量 c 和 n 0 , 使 得 对 所 有 n ≥ n 0 , 有 0 ≤ f ( n ) ≤ c g ( n ) }
含义是:对于足够大的
n
n
n
f
(
n
)
f(n)
f ( n )
c
g
(
n
)
cg(n)
c g ( n )
g
(
n
)
g(n)
g ( n )
f
(
n
)
f(n)
f ( n )
注意:在很多教材中,会发现用
O
(
g
(
n
)
)
O(g(n))
O ( g ( n ) )
Θ
(
g
(
n
)
)
\Theta(g(n))
Θ ( g ( n ) )
下图形象地表示了渐近上界的形式:
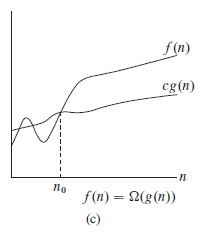
Ω
\Omega
Ω 定义:对于一个给定的函数
g
(
n
)
g(n)
g ( n )
Ω
(
g
(
n
)
)
\Omega(g(n))
Ω ( g ( n ) ) 函数的集合 :
:
存
在
正
常
量
和
,
使
得
对
所
有
有
Ω
(
g
(
n
)
)
=
{
f
(
n
)
:
存
在
正
常
量
c
和
n
0
,
使
得
对
所
有
n
≥
n
0
,
有
0
≤
c
g
(
n
)
≤
f
(
n
)
}
:存在正常量和,使得对所有有\Omega(g(n))=\{f(n):存在正常量c和n_0,使得对所有n\geq n_0,有0\leq cg(n)\leq f(n)\}
: 存 在 正 常 量 和 , 使 得 对 所 有 有 Ω ( g ( n ) ) = { f ( n ) : 存 在 正 常 量 c 和 n 0 , 使 得 对 所 有 n ≥ n 0 , 有 0 ≤ c g ( n ) ≤ f ( n ) }
含义是:对于足够大的
n
n
n
f
(
n
)
f(n)
f ( n )
c
g
(
n
)
cg(n)
c g ( n )
g
(
n
)
g(n)
g ( n )
f
(
n
)
f(n)
f ( n )
下图形象地表示了渐近下界的形式:
o
o
o
ω
\omega
ω 定义:对于一个给定的函数
g
(
n
)
g(n)
g ( n )
o
(
g
(
n
)
)
o(g(n))
o ( g ( n ) ) 函数的集合 :
:
对
任
何
正
常
量
,
存
在
常
量
,
使
得
对
所
有
有
o
(
g
(
n
)
)
=
{
f
(
n
)
:
对
任
何
正
常
量
c
>
0
,
存
在
常
量
n
0
>
0
,
使
得
对
所
有
n
≥
n
0
,
有
0
≤
f
(
n
)
≤
c
g
(
n
)
}
:对任何正常量,存在常量,使得对所有有o(g(n))=\{f(n):对任何正常量c>0,存在常量n_0>0,使得对所有n\geq n_0,有0\leq f(n)\leq cg(n)\}
: 对 任 何 正 常 量 , 存 在 常 量 , 使 得 对 所 有 有 o ( g ( n ) ) = { f ( n ) : 对 任 何 正 常 量 c > 0 , 存 在 常 量 n 0 > 0 , 使 得 对 所 有 n ≥ n 0 , 有 0 ≤ f ( n ) ≤ c g ( n ) }
含义可类比于
O
(
g
(
n
)
)
O(g(n))
O ( g ( n ) )
f
(
n
)
f(n)
f ( n )
g
(
n
)
g(n)
g ( n ) 低一级幂次 。如
2
n
2n
2 n
3
n
2
3n^2
3 n 2
定义:对于一个给定的函数
g
(
n
)
g(n)
g ( n )
ω
(
g
(
n
)
)
\omega(g(n))
ω ( g ( n ) ) 函数的集合 :
:
对
任
何
正
常
量
,
存
在
常
量
,
使
得
对
所
有
有
ω
(
g
(
n
)
)
=
{
f
(
n
)
:
对
任
何
正
常
量
c
>
0
,
存
在
常
量
n
0
>
0
,
使
得
对
所
有
n
≥
n
0
,
有
0
≤
c
g
(
n
)
≤
f
(
n
)
}
:对任何正常量,存在常量,使得对所有有\omega(g(n))=\{f(n):对任何正常量c>0,存在常量n_0>0,使得对所有n\geq n_0,有0\leq cg(n)\leq f(n)\}
: 对 任 何 正 常 量 , 存 在 常 量 , 使 得 对 所 有 有 ω ( g ( n ) ) = { f ( n ) : 对 任 何 正 常 量 c > 0 , 存 在 常 量 n 0 > 0 , 使 得 对 所 有 n ≥ n 0 , 有 0 ≤ c g ( n ) ≤ f ( n ) }
含义可类比于
Ω
(
g
(
n
)
)
\Omega(g(n))
Ω ( g ( n ) )
f
(
n
)
f(n)
f ( n )
g
(
n
)
g(n)
g ( n ) 高一级幂次 。如
2
n
3
2n^3
2 n 3
3
n
2
3n^2
3 n 2
(1)对任意整数n,存在以下性质:
(2)对于某个常量k,如果存在
f
(
n
)
f(n)
f ( n )
(3)多项式与指数的增长率可以通过以下事实相关联。对于所有使得
a
>
1
a>1
a > 1
据此可知
因此,任意底大于1的指数函数增长都比多项式函数快。
(4)在(3)的第一个等式中,用
l
g
n
lgn
l g n
n
n
n
2
a
2^a
2 a
a
a
a
可以得到,对于任意常量
a
>
0
a>0
a > 0
因此,任意正的多项式函数都比任意多对数函数增长快。
(5)阶乘函数的弱上界为
n
!
<
=
n
n
n!<=n^n
n ! < = n n
n
n
n
n
n
n
n
n
n
假设
f
(
n
)
f(n)
f ( n )
g
(
n
)
g(n)
g ( n )
Θ
\Theta
Θ
m
a
x
(
f
(
n
)
,
g
(
n
)
)
=
Θ
(
f
(
n
)
+
g
(
n
)
)
max(f(n),g(n))=\Theta(f(n)+g(n))
m a x ( f ( n ) , g ( n ) ) = Θ ( f ( n ) + g ( n ) )
存在
c
1
=
1
/
2
c_1=1/2
c 1 = 1 / 2
,
m
a
x
(
f
(
n
)
,
g
(
n
)
≥
1
/
2
(
f
(
n
)
+
g
(
n
)
,max(f(n),g(n)\geq 1/2(f(n)+g(n)
, m a x ( f ( n ) , g ( n ) ≥ 1 / 2 ( f ( n ) + g ( n )
存在
c
2
=
1
c_2 = 1
c 2 = 1
,
m
a
x
(
f
(
n
)
,
g
(
n
)
≤
(
f
(
n
)
+
g
(
n
)
,max(f(n),g(n)\leq (f(n)+g(n)
, m a x ( f ( n ) , g ( n ) ≤ ( f ( n ) + g ( n )
所以根据
Θ
\Theta
Θ
,
m
a
x
(
f
(
n
)
,
g
(
n
)
=
Θ
(
f
(
n
)
+
g
(
n
)
,max(f(n),g(n)=\Theta (f(n)+g(n)
, m a x ( f ( n ) , g ( n ) = Θ ( f ( n ) + g ( n )
证明:对任意实常数
a
a
a
b
b
b
b
>
0
b>0
b > 0
(
n
+
a
)
b
=
Θ
(
n
b
)
(n+a)^b=\Theta(n^b)
( n + a ) b = Θ ( n b )
(
n
+
a
)
b
=
n
b
+
c
1
n
b
−
1
+
c
2
n
b
−
2
+
⋯
+
a
b
=
n
b
+
Θ
(
n
b
−
1
)
=
Θ
(
n
b
)
(n+a)^b = n^b + c_1 n^{b-1} + c_2 n^{b-2} + \cdots + a^b=n^b+\Theta(n^{b-1})=\Theta (n^b)
( n + a ) b = n b + c 1 n b − 1 + c 2 n b − 2 + ⋯ + a b = n b + Θ ( n b − 1 ) = Θ ( n b )
解释为什么 “算法A的运行时间至少是
O
(
n
2
)
O(n^2)
O ( n 2 )
记号
O
(
)
O()
O ( )
O
(
)
O()
O ( )
O
(
n
)
O(n)
O ( n )
2
(
n
+
1
)
=
O
(
2
n
)
2^{(n+1)}=O(2^n)
2 ( n + 1 ) = O ( 2 n )
2
(
2
n
)
=
O
(
2
n
)
2^{(2n)}=O(2^n)
2 ( 2 n ) = O ( 2 n )
1)证明:存在
c
=
2
,
n
0
>
0
c=2, n_0>0
c = 2 , n 0 > 0
对
于
所
有
0
≤
2
n
+
1
≤
c
2
n
对
于
所
有
n
≥
n
0
对于所有0 \le 2^{n+1} \le c2^n 对于所有n \ge n_0
对 于 所 有 0 ≤ 2 n + 1 ≤ c 2 n 对 于 所 有 n ≥ n 0
2
2
n
=
O
(
2
n
)
2^{2n} = O(2^n)
2 2 n = O ( 2 n )
2)要使其成立,则
c
=
2
2
n
2
n
=
2
n
c=\frac{2^{2n}}{2^n}=2^n
c = 2 n 2 2 n = 2 n
证明定理3.1
对
任
意
两
个
函
数
和
,
我
们
有
,
当
且
仅
当
且
对
任
意
两
个
函
数
f
(
n
)
和
g
(
n
)
,
我
们
有
f
(
n
)
=
Θ
(
g
(
n
)
)
,
当
且
仅
当
f
(
n
)
=
O
(
g
(
n
)
)
且
f
(
n
)
=
Ω
(
g
(
n
)
)
对任意两个函数和,我们有,当且仅当且对任意两个函数f(n)和g(n),我们有f(n)=\Theta(g(n)),当且仅当f(n)=O(g(n))且f(n)=\Omega(g(n))
对 任 意 两 个 函 数 和 , 我 们 有 , 当 且 仅 当 且 对 任 意 两 个 函 数 f ( n ) 和 g ( n ) , 我 们 有 f ( n ) = Θ ( g ( n ) ) , 当 且 仅 当 f ( n ) = O ( g ( n ) ) 且 f ( n ) = Ω ( g ( n ) )
由
f
(
n
)
=
O
(
g
(
n
)
)
f(n)=O(g(n))
f ( n ) = O ( g ( n ) )
n
≥
n
1
n\geq n_1
n ≥ n 1
0
≤
f
(
n
)
≤
c
1
g
(
n
)
0\leq f(n)\leq c_1g(n)
0 ≤ f ( n ) ≤ c 1 g ( n )
由
f
(
n
)
=
Ω
(
g
(
n
)
)
f(n)=\Omega(g(n))
f ( n ) = Ω ( g ( n ) )
n
≥
n
2
n\geq n_2
n ≥ n 2
0
≤
c
2
g
(
n
)
≤
f
(
n
)
0\leq c_2g(n)\leq f(n)
0 ≤ c 2 g ( n ) ≤ f ( n )
所以,当
n
>
=
m
a
x
(
n
1
,
n
2
)
n>=max(n_1,n_2)
n > = m a x ( n 1 , n 2 )
0
≤
c
2
g
(
n
)
<
=
f
(
n
)
<
=
c
1
g
(
n
)
0\leq c_2g(n)<=f(n)<=c_1g(n)
0 ≤ c 2 g ( n ) < = f ( n ) < = c 1 g ( n )
证明:一个算法的运行时间是
Θ
(
g
(
n
)
)
\Theta(g(n))
Θ ( g ( n ) )
O
(
g
(
n
)
)
O(g(n))
O ( g ( n ) )
Ω
(
g
(
n
)
)
\Omega(g(n))
Ω ( g ( n ) )
最坏情况下复杂度为
O
(
g
(
n
)
)
O(g(n))
O ( g ( n ) )
O
(
g
(
n
)
)
O(g(n))
O ( g ( n ) )
Θ
(
g
(
n
)
)
\Theta(g(n))
Θ ( g ( n ) )
Ω
(
g
(
n
)
)
\Omega(g(n))
Ω ( g ( n ) )
Θ
(
g
(
n
)
)
\Theta (g(n))
Θ ( g ( n ) )
证明
o
(
g
(
n
)
)
∩
ω
(
g
(
n
)
)
o(g(n))\cap \omega(g(n))
o ( g ( n ) ) ∩ ω ( g ( n ) )
f
(
n
)
=
o
(
g
(
n
)
)
f(n)=o(g(n))
f ( n ) = o ( g ( n ) )
c
,
n
0
c,n_0
c , n 0
n
≥
n
0
n \ge n_0
n ≥ n 0
对
于
所
有
0
≤
f
(
n
)
<
c
g
(
n
)
对
于
所
有
n
≥
n
0
对于所有0 \le f(n) < cg(n) 对于所有n \ge n_0
对 于 所 有 0 ≤ f ( n ) < c g ( n ) 对 于 所 有 n ≥ n 0
f
(
n
)
=
ω
(
g
(
n
)
)
f(n)=\omega (g(n))
f ( n ) = ω ( g ( n ) )
c
,
n
0
c,n_0
c , n 0
n
≥
n
0
n \ge n_0
n ≥ n 0
0
≤
c
g
(
n
)
<
f
(
n
)
0 \le cg(n) < f(n)
0 ≤ c g ( n ) < f ( n )
o
(
g
(
n
)
)
∩
ω
(
g
(
n
)
)
=
∅
o(g(n)) \cap \omega (g(n)) =\varnothing
o ( g ( n ) ) ∩ ω ( g ( n ) ) = ∅
可以将我们的表示法扩展到有两个参数n和m的情形,其中
n
n
n
m
m
m
,
g
(
n
,
m
)
,
O
(
g
(
n
,
m
)
)
,g(n,m),O(g(n,m))
, g ( n , m ) , O ( g ( n , m ) )
存
在
正
整
数
和
,
使
对
所
有
或
,
有
O
(
g
(
n
,
m
)
)
=
{
f
(
n
,
m
)
:
存
在
正
整
数
c
,
n
0
和
m
0
,
使
对
所
有
n
≥
n
0
或
m
≥
m
0
,
有
0
≤
f
(
n
,
m
)
≤
c
g
(
n
,
m
)
}
存在正整数和,使对所有或,有O(g(n,m))=\{f(n,m): 存在正整数c,n_0和m_0,使对所有n\geq n_0或m\geq m_0,有0\leq f(n,m)\leq cg(n,m)\}
存 在 正 整 数 和 , 使 对 所 有 或 , 有 O ( g ( n , m ) ) = { f ( n , m ) : 存 在 正 整 数 c , n 0 和 m 0 , 使 对 所 有 n ≥ n 0 或 m ≥ m 0 , 有 0 ≤ f ( n , m ) ≤ c g ( n , m ) }
给出对应的
Ω
(
g
(
n
,
m
)
)
\Omega(g(n,m))
Ω ( g ( n , m ) )
Θ
(
g
(
n
,
m
)
)
\Theta(g(n,m))
Θ ( g ( n , m ) )
存
在
正
整
数
和
,
使
对
所
有
或
,
有
Ω
(
g
(
n
,
m
)
)
=
{
f
(
n
,
m
)
:
存
在
正
整
数
c
,
n
0
和
m
0
,
使
对
所
有
n
≥
n
0
或
m
≥
m
0
,
有
0
≤
c
g
(
n
,
m
)
≤
f
(
n
,
m
)
}
存在正整数和,使对所有或,有\Omega(g(n,m))=\{f(n,m): 存在正整数c,n_0和m_0,使对所有n\geq n_0或m\geq m_0,有0\leq cg(n,m)\leq f(n,m)\}
存 在 正 整 数 和 , 使 对 所 有 或 , 有 Ω ( g ( n , m ) ) = { f ( n , m ) : 存 在 正 整 数 c , n 0 和 m 0 , 使 对 所 有 n ≥ n 0 或 m ≥ m 0 , 有 0 ≤ c g ( n , m ) ≤ f ( n , m ) }
2)
存
在
正
整
数
和
,
使
对
所
有
或
有
Θ
(
g
(
n
,
m
)
)
=
{
f
(
n
,
m
)
:
存
在
正
整
数
c
1
,
c
2
,
n
0
和
m
0
,
使
对
所
有
n
≥
n
0
或
m
≥
m
0
,
有
c
1
g
(
n
,
m
)
≤
f
(
n
,
m
)
≤
c
2
g
(
n
,
m
)
}
存在正整数和,使对所有或有\Theta(g(n,m))=\{f(n,m): 存在正整数c_1,c_2,n_0和m_0,使对所有n\geq n_0或m\geq m_0, 有c_1g(n,m)\leq f(n,m)\leq c_2g(n,m)\}
存 在 正 整 数 和 , 使 对 所 有 或 有 Θ ( g ( n , m ) ) = { f ( n , m ) : 存 在 正 整 数 c 1 , c 2 , n 0 和 m 0 , 使 对 所 有 n ≥ n 0 或 m ≥ m 0 , 有 c 1 g ( n , m ) ≤ f ( n , m ) ≤ c 2 g ( n , m ) }
证明:若
f
(
n
)
f(n)
f ( n )
g
(
n
)
g(n)
g ( n )
f
(
n
)
+
g
(
n
)
f(n)+g(n)
f ( n ) + g ( n )
f
(
g
(
n
)
)
f(g(n))
f ( g ( n ) )
f
(
n
)
f(n)
f ( n )
g
(
n
)
g(n)
g ( n )
f
(
n
)
⋅
g
(
n
)
f(n)\cdot g(n)
f ( n ) ⋅ g ( n )
由于
f
(
n
)
f(n)
f ( n )
g
(
n
)
g(n)
g ( n )
x
1
<
x
2
x_1 < x_2
x 1 < x 2
f
(
x
1
)
<
f
(
x
2
)
f(x_1) < f(x_2)
f ( x 1 ) < f ( x 2 )
g
(
x
1
)
<
g
(
x
2
)
g(x_1) < g(x_2)
g ( x 1 ) < g ( x 2 )
f
(
x
1
)
+
g
(
x
1
)
<
f
(
x
2
)
+
g
(
x
2
)
f(x_1)+g(x_1) < f(x_2)+g(x_2)
f ( x 1 ) + g ( x 1 ) < f ( x 2 ) + g ( x 2 )
f
(
g
(
x
1
)
)
<
f
(
g
(
x
2
)
)
f(g(x_1)) < f(g(x_2))
f ( g ( x 1 ) ) < f ( g ( x 2 ) )
f
(
x
1
)
∗
g
(
x
1
)
<
f
(
x
2
)
∗
g
(
x
2
)
f(x_1)*g(x_1) < f(x_2)*g(x_2)
f ( x 1 ) ∗ g ( x 1 ) < f ( x 2 ) ∗ g ( x 2 )
证明等式3.16
a
log
b
c
=
c
log
b
a
\LARGE{a^{\log_bc} = c^{\log_ba}}
a log b c = c log b a
lg
a
log
b
c
=
log
b
c
lg
a
=
lg
a
lg
c
lg
b
\lg {a^{\log_bc}}=\log_bc \lg a=\frac {\lg a \lg c} {\lg b}
lg a log b c = log b c lg a = lg b lg a lg c
lg
c
log
b
a
=
log
b
a
lg
c
=
lg
a
lg
c
lg
b
\lg {c^{\log_ba}}=\log_ba \lg c=\frac {\lg a \lg c} {\lg b}
lg c log b a = log b a lg c = lg b lg a lg c
⇒
a
log
b
c
=
c
log
b
a
\Rightarrow a^{\log_bc} = c^{\log_ba}
⇒ a log b c = c log b a
证明等式3.19
l
g
(
n
!
)
=
Θ
(
n
l
g
n
)
lg(n!)=\Theta(nlgn)
l g ( n ! ) = Θ ( n l g n )
n
!
=
ω
(
2
n
)
n!=\omega (2^n)
n ! = ω ( 2 n )
n
!
=
o
(
n
n
)
n!=o(n^n)
n ! = o ( n n )
证明
lg
(
n
!
)
=
Θ
(
n
lg
n
)
\lg {(n!)} = \Theta (n \lg n)
lg ( n ! ) = Θ ( n lg n )
lg
n
!
=
∑
i
=
1
n
lg
i
<
∑
i
=
1
n
lg
n
=
n
lg
n
\lg {n!} = \sum_{i=1}^n{\lg i} < \sum_{i=1}^n{\lg n} = n \lg n
lg n ! = i = 1 ∑ n lg i < i = 1 ∑ n lg n = n lg n
∑
i
=
1
n
lg
i
=
∑
i
=
1
n
/
2
[
lg
i
+
lg
(
n
−
i
)
]
=
∑
i
=
1
n
/
2
[
lg
i
(
n
−
i
)
]
>
∑
i
=
1
n
/
2
lg
n
2
4
=
n
lg
n
−
n
>
1
2
n
lg
n
\sum_{i=1}^n{\lg i} = \sum_{i=1}^{n/2} {[\lg i + \lg {(n-i)}]} = \sum_{i=1}^{n/2} {[\lg {i (n-i)}]} > \sum_{i=1}^{n/2} {\lg {\frac {n^2}{4}}} = n \lg n - n > \frac 12 n \lg n
i = 1 ∑ n lg i = i = 1 ∑ n / 2 [ lg i + lg ( n − i ) ] = i = 1 ∑ n / 2 [ lg i ( n − i ) ] > i = 1 ∑ n / 2 lg 4 n 2 = n lg n − n > 2 1 n lg n
⇒
lg
(
n
!
)
=
Θ
(
n
lg
n
)
\Rightarrow \lg {(n!)} = \Theta (n \lg n)
⇒ lg ( n ! ) = Θ ( n lg n )
证明
n
!
=
ω
(
2
n
)
n! = \omega (2^n)
n ! = ω ( 2 n )
当
时
,
∵
当
n
>
4
时
,
i
(
n
−
i
)
>
2
2
当时,\because 当n > 4时,i (n-i) > 2^2
当 时 , ∵ 当 n > 4 时 , i ( n − i ) > 2 2
∴
n
!
=
∏
i
=
1
n
/
2
i
(
n
−
i
)
>
∏
i
=
1
n
/
2
2
2
=
2
n
\therefore n! = \prod_{i=1}^{n/2} {i (n-i)} > \prod_{i=1}^{n/2} {2^2} = 2^n
∴ n ! = i = 1 ∏ n / 2 i ( n − i ) > i = 1 ∏ n / 2 2 2 = 2 n
∴
n
!
=
ω
(
2
n
)
\therefore n! = \omega (2^n)
∴ n ! = ω ( 2 n )
证明
n
!
=
o
(
n
n
)
n! = o (n^n)
n ! = o ( n n )
当
时
,
∵
当
n
>
1
时
,
n
!
=
∏
i
=
1
n
i
<
∏
i
=
1
n
n
=
n
n
当时,\because 当n > 1时,n! = \prod_{i=1}^n i < \prod_{i=1}^n n = n^n
当 时 , ∵ 当 n > 1 时 , n ! = i = 1 ∏ n i < i = 1 ∏ n n = n n
∴
n
!
=
o
(
n
n
)
\therefore n! = o (n^n)
∴ n ! = o ( n n )
函数
⌈
lg
n
⌉
!
\lceil \lg n \rceil!
⌈ lg n ⌉ !
证明
f
(
n
)
f(n)
f ( n )
lg
f
(
n
)
=
O
(
lg
n
)
\lg {f(n)} = O (\lg n)
lg f ( n ) = O ( lg n )
f
(
n
)
f(n)
f ( n )
c
,
k
,
n
0
c,k,n_0
c , k , n 0
n
>
n
0
n > n_0
n > n 0
f
(
n
)
<
c
n
k
f(n) < c n^k
f ( n ) < c n k
lg
f
(
n
)
<
k
c
lg
n
\lg {f(n)} < k c \lg n
lg f ( n ) < k c lg n
lg
f
(
n
)
=
O
(
lg
n
)
\lg {f(n)} = O (\lg n)
lg f ( n ) = O ( lg n )
⌈
lg
n
⌉
!
\lceil \lg n \rceil !
⌈ lg n ⌉ !
lg
(
⌈
lg
n
⌉
!
)
=
Θ
(
⌈
lg
n
⌉
lg
⌈
lg
n
⌉
)
≥
Θ
(
lg
n
lg
lg
n
)
=
ω
(
lg
n
)
\lg {(\lceil \lg n \rceil !)} = \Theta (\lceil \lg n \rceil \lg {\lceil \lg n \rceil}) \geq \Theta (\lg n \lg {\lg n}) = \omega (\lg n)
lg ( ⌈ lg n ⌉ ! ) = Θ ( ⌈ lg n ⌉ lg ⌈ lg n ⌉ ) ≥ Θ ( lg n lg lg n ) = ω ( lg n )
⌈
lg
n
⌉
!
\lceil \lg n \rceil !
⌈ lg n ⌉ !
对于 $ \lceil \lg {\lg n} \rceil ! $ 我们有 KaTeX parse error: Expected 'EOF', got '\eqalign' at position 1: \̲e̲q̲a̲l̲i̲g̲n̲ ̲{ & \lg {(\lcei… 。 $ \lceil \lg {\lg n} \rceil ! $ 多项式有界
如下两个函数中,哪一个渐近更大些:
lg
(
lg
∗
n
)
\lg(\lg^* n)
lg ( lg ∗ n )
lg
∗
(
lg
n
)
\lg^*(\lg n)
lg ∗ ( lg n )
将
lg
∗
(
n
)
\lg^*(n)
lg ∗ ( n ) (\lg(n))$ 就是先对
n
n
n (lg(n)) = lg^*(n) - 1$。
故:
当
时
lg
∗
lg
n
=
lg
∗
n
−
1
>
lg
lg
∗
n
,
当
lg
∗
n
>
2
时
当时\lg^* {\lg n} = \lg^* n - 1 > \lg {\lg^* n},当\lg^* n > 2时
当 时 lg ∗ lg n = lg ∗ n − 1 > lg lg ∗ n , 当 lg ∗ n > 2 时
证明:黄金分割率
ϕ
\phi
ϕ
ϕ
^
\hat \phi
ϕ ^
x
2
=
x
+
1
x^2=x+1
x 2 = x + 1
ϕ
2
=
(
1
+
5
2
)
2
=
3
+
5
2
=
ϕ
+
1
\phi ^2 = (\frac {1+\sqrt 5} {2})^2 = \frac {3 + \sqrt5} {2} = \phi + 1
ϕ 2 = ( 2 1 + 5
) 2 = 2 3 + 5
= ϕ + 1
ϕ
^
2
=
(
1
−
5
2
)
2
=
3
−
5
2
=
ϕ
^
+
1
\hat {\phi} ^2 = (\frac {1-\sqrt 5} {2})^2 = \frac {3 - \sqrt5} {2} = \hat {\phi} + 1
ϕ ^ 2 = ( 2 1 − 5
) 2 = 2 3 − 5
= ϕ ^ + 1
用归纳法证明:第
i
i
i
F
i
=
ϕ
i
−
ϕ
^
i
5
\LARGE F_i=\frac {\phi ^i -\hat\phi^i}{\sqrt5}
F i = 5
ϕ i − ϕ ^ i
ϕ
\phi
ϕ
ϕ
^
\hat\phi
ϕ ^
证明:
ϕ
0
−
ϕ
^
0
5
=
0
=
F
0
\frac {\phi ^0 - \hat {\phi}^0}{\sqrt 5} = 0 = F_0
5
ϕ 0 − ϕ ^ 0 = 0 = F 0
ϕ
1
−
ϕ
^
1
5
=
1
=
F
1
\frac {\phi ^1 - \hat {\phi}^1}{\sqrt 5} = 1 = F_1
5
ϕ 1 − ϕ ^ 1 = 1 = F 1
假设当i = k-1和i = k时都满足公式,则当i = k+1,
F
k
+
1
=
F
k
+
F
k
−
1
=
(
ϕ
k
+
ϕ
k
−
1
)
−
(
ϕ
^
k
+
ϕ
^
k
−
1
)
5
=
ϕ
k
−
1
(
ϕ
+
1
)
−
ϕ
^
k
−
1
(
ϕ
^
+
1
)
5
F_{k+1}=F_k + F_{k-1} = \frac {(\phi ^k + \phi ^{k-1}) - (\hat {\phi}^k+\hat {\phi}^{k-1})}{\sqrt 5}=\frac {\phi^{k-1}(\phi + 1)-\hat {\phi}^{k-1}(\hat {\phi} + 1)}{\sqrt 5}
F k + 1 = F k + F k − 1 = 5
( ϕ k + ϕ k − 1 ) − ( ϕ ^ k + ϕ ^ k − 1 ) = 5
ϕ k − 1 ( ϕ + 1 ) − ϕ ^ k − 1 ( ϕ ^ + 1 )
(
ϕ
+
1
)
=
ϕ
2
(\phi+1)=\phi^2
( ϕ + 1 ) = ϕ 2
(
ϕ
^
+
1
)
=
ϕ
^
2
(\hat\phi+1)=\hat\phi^2
( ϕ ^ + 1 ) = ϕ ^ 2
得
ϕ
k
−
1
(
ϕ
+
1
)
−
ϕ
^
k
−
1
(
ϕ
^
+
1
)
5
=
ϕ
k
+
1
−
ϕ
^
k
+
1
5
\frac {\phi^{k-1}(\phi + 1)-\hat {\phi}^{k-1}(\hat {\phi} + 1)}{\sqrt 5}=\frac {\phi ^{k+1} - \hat {\phi}^{k+1}}{\sqrt 5}
5
ϕ k − 1 ( ϕ + 1 ) − ϕ ^ k − 1 ( ϕ ^ + 1 ) = 5
ϕ k + 1 − ϕ ^ k + 1
证明:
k
ln
k
=
Θ
(
n
)
k\ln k=\Theta(n)
k ln k = Θ ( n )
k
=
Θ
(
n
/
ln
n
)
k=\Theta(n/\ln n)
k = Θ ( n / ln n )
这题要用到性质
g
(
n
)
=
Θ
(
f
(
n
)
)
⇔
f
(
n
)
=
Θ
(
g
(
n
)
)
g(n) = \Theta (f(n)) \Leftrightarrow f(n) = \Theta (g(n))
g ( n ) = Θ ( f ( n ) ) ⇔ f ( n ) = Θ ( g ( n ) )
k
ln
k
=
Θ
(
n
)
⇔
n
=
Θ
(
k
ln
k
)
k \ln k = \Theta (n) \Leftrightarrow n = \Theta (k \ln k)
k ln k = Θ ( n ) ⇔ n = Θ ( k ln k )
k
=
Θ
(
n
/
ln
n
)
k = \Theta (n / \ln n)
k = Θ ( n / ln n )
n
/
ln
n
=
Θ
(
k
)
n / \ln n = \Theta (k)
n / ln n = Θ ( k )
n
ln
n
=
Θ
(
k
ln
k
ln
(
k
ln
k
)
)
=
Θ
(
k
ln
k
ln
k
)
=
Θ
(
k
)
\frac {n}{\ln n} = \Theta (\frac {k \ln k} {\ln {(k \ln k})}) = \Theta (\frac {k \ln k} {\ln k}) = \Theta (k)
ln n n = Θ ( ln ( k ln k ) k ln k ) = Θ ( ln k k ln k ) = Θ ( k )
假设
p
(
n
)
=
∑
i
=
0
d
a
i
n
i
p(n)=\sum^d_{i=0}a_in^i
p ( n ) = ∑ i = 0 d a i n i
n
n
n
d
d
d
a
d
>
0
a_d>0
a d > 0
k
k
k
a. 若
k
≥
d
k\ge d
k ≥ d
p
(
n
)
=
O
(
n
k
)
p(n)=O(n^k)
p ( n ) = O ( n k )
b. 若
k
≤
d
k\le d
k ≤ d
p
(
n
)
=
Ω
(
n
k
)
p(n)=\Omega(n^k)
p ( n ) = Ω ( n k )
c. 若
k
=
d
k=d
k = d
p
(
n
)
=
Θ
(
n
k
)
p(n)=\Theta(n^k)
p ( n ) = Θ ( n k )
d. 若
k
>
d
k> d
k > d
p
(
n
)
=
o
(
n
k
)
p(n)=o(n^k)
p ( n ) = o ( n k )
e. 若
k
<
d
k< d
k < d
p
(
n
)
=
ω
(
n
k
)
p(n)=\omega(n^k)
p ( n ) = ω ( n k )
a.
P
(
n
)
=
∑
i
=
0
d
a
i
n
i
=
n
d
∑
i
=
0
d
a
i
n
i
−
d
≤
n
d
∑
i
=
0
d
a
i
≤
c
n
d
≤
c
n
k
P(n) = \sum_{i=0}^d {a_i n^i} = n^d \sum_{i=0}^d {a_i n^{i-d}} \le n^d \sum_{i=0}^d {a_i} \le cn^d\le cn^k
P ( n ) = i = 0 ∑ d a i n i = n d i = 0 ∑ d a i n i − d ≤ n d i = 0 ∑ d a i ≤ c n d ≤ c n k
b.
P
(
n
)
=
∑
i
=
0
d
a
i
n
i
≥
n
d
≥
c
n
d
≥
c
n
k
P(n) = \sum_{i=0}^d {a_i n^i} \ge n^d \ge cn^d\ge cn_k
P ( n ) = i = 0 ∑ d a i n i ≥ n d ≥ c n d ≥ c n k
c. 由前两问可证。
d.
P
(
n
)
=
∑
i
=
0
d
a
i
n
i
=
n
d
∑
i
=
0
d
a
i
n
i
−
d
<
n
d
∑
i
=
0
d
a
i
<
c
n
d
≤
c
n
k
P(n) = \sum_{i=0}^d {a_i n^i} = n^d \sum_{i=0}^d {a_i n^{i-d}}< n^d \sum_{i=0}^d {a_i} <cn^d\le cn^k
P ( n ) = i = 0 ∑ d a i n i = n d i = 0 ∑ d a i n i − d < n d i = 0 ∑ d a i < c n d ≤ c n k
e.
P
(
n
)
=
∑
i
=
0
d
a
i
n
i
>
n
d
>
c
n
d
>
c
n
k
P(n) = \sum_{i=0}^d {a_i n^i} >n^d > cn^d> cn_k
P ( n ) = i = 0 ∑ d a i n i > n d > c n d > c n k
为下标中的每对表达式(A,B)指出A是否是B的
、
、
、
或
O
、
o
、
Ω
、
ω
或
Θ
、、、或O、o、\Omega、\omega或\Theta
、 、 、 或 O 、 o 、 Ω 、 ω 或 Θ
、
且
k
≥
1
、
ϵ
>
0
且
c
>
1
、且k\ge1、\epsilon>0且c>1
、 且 k ≥ 1 、 ϵ > 0 且 c > 1
A
B
O
O
O
o
o
o
Ω
\Omega
Ω
ω
\omega
ω
Θ
\Theta
Θ
lg
k
n
\lg^k n
lg k n
n
ϵ
n^{\epsilon}
n ϵ 否
否
是
是
否
n
k
n^k
n k
c
n
c^n
c n 否
否
是
是
否
n
\sqrt n
n
n
sin
n
n^{\sin n}
n sin n 否
否
否
否
否
2
n
2^n
2 n
2
n
/
2
2^{n/2}
2 n / 2 是
是
否
否
否
n
lg
c
n^{\lg c}
n lg c
c
lg
n
c^{\lg n}
c lg n 是
否
是
否
是
lg
(
n
!
)
\lg {(n!)}
lg ( n ! )
lg
(
n
n
)
\lg {(n^n)}
lg ( n n ) 是
否
是
否
是
a.根据增长的阶来排序下面的函数,即求出满足
g
1
=
Ω
(
g
2
)
g_1=\Omega(g_2)
g 1 = Ω ( g 2 )
,
g
2
=
Ω
(
g
3
)
,
⋯
,g_2=\Omega(g_3),\cdots
, g 2 = Ω ( g 3 ) , ⋯
g
29
=
Ω
(
g
30
)
g_{29}=\Omega(g_{30})
g 2 9 = Ω ( g 3 0 )
g
1
,
g
2
,
⋯
 
,
g
30
g_1,g_2,\cdots,g_{30}
g 1 , g 2 , ⋯ , g 3 0
f
(
n
)
f(n)
f ( n )
g
(
n
)
g(n)
g ( n )
f
(
n
)
=
Θ
(
g
(
n
)
)
f(n)=\Theta(g(n))
f ( n ) = Θ ( g ( n ) )
lg
(
lg
∗
n
)
\lg(\lg^*n)
lg ( lg ∗ n )
2
lg
n
2^{\lg^n}
2 lg n
(
2
)
lg
n
(\sqrt{2})^{\lg{n}}
( 2
) lg n
n
2
n^2
n 2
n
!
n!
n !
(
lg
n
)
!
(\lg{n})!
( lg n ) !
(
3
2
)
n
(\frac{3}{2})^n
( 2 3 ) n
n
3
n^3
n 3
lg
2
n
\lg^2{n}
lg 2 n
lg
(
n
!
)
\lg(n!)
lg ( n ! )
2
2
n
2^{2^n}
2 2 n
n
1
/
lg
n
n^{1/\lg{n}}
n 1 / lg n
ln
ln
n
\ln{\ln{n}}
ln ln n
lg
n
\lg^n
lg n
n
⋅
2
n
n \cdot 2^n
n ⋅ 2 n
n
lg
lg
n
n^{\lg\lg{n}}
n lg lg n
ln
n
\ln{n}
ln n
1
1
1
2
lg
n
2^{\lg{n}}
2 lg n
(
lg
n
)
lg
n
(\lg{n})^{\lg{n}}
( lg n ) lg n
e
n
e^n
e n
4
lg
n
4^{\lg{n}}
4 lg n
(
n
+
1
)
!
(n + 1)!
( n + 1 ) !
lg
n
\sqrt{\lg{n}}
lg n
lg
∗
(
lg
n
)
\lg^*(\lg{n})
lg ∗ ( lg n )
2
2
lg
n
2^{\sqrt{2\lg{n}}}
2 2 lg n
n
n
n
2
n
2^n
2 n
n
lg
n
n\lg{n}
n lg n
2
2
n
+
1
2^{2^{n + 1}}
2 2 n + 1
2
2
n
+
1
>
2
2
n
>
(
n
+
1
)
!
>
n
!
>
e
n
>
n
2
n
>
2
n
>
(
3
/
2
)
n
>
(
lg
n
)
lg
n
=
n
lg
lg
n
>
(
lg
n
)
!
2^{2^{n+1}} > 2^{2^n} > (n+1)! > n! > e^n > n 2^n > 2^n > (3/2)^n > (\lg n)^{\lg n} = n^{\lg {\lg n}} > (\lg n)!
2 2 n + 1 > 2 2 n > ( n + 1 ) ! > n ! > e n > n 2 n > 2 n > ( 3 / 2 ) n > ( lg n ) lg n = n lg lg n > ( lg n ) !
>
n
3
>
n
2
=
4
lg
n
>
n
lg
n
=
lg
(
n
!
)
>
n
=
2
lg
n
>
(
2
)
lg
n
=
n
>
2
2
lg
n
>
lg
2
n
>
ln
n
> n^3 > n^2 = 4^{\lg n} > n \lg n= \lg {(n!)} > n = 2^{\lg n} > (\sqrt 2)^{\lg n} = \sqrt n > 2^{\sqrt {2\lg n}} > \lg^2 n > \ln n
> n 3 > n 2 = 4 lg n > n lg n = lg ( n ! ) > n = 2 lg n > ( 2
) lg n = n
> 2 2 lg n
> lg 2 n > ln n
>
lg
n
>
ln
ln
n
>
2
lg
∗
n
>
lg
∗
n
=
lg
∗
(
lg
n
)
>
lg
(
lg
∗
n
)
>
n
1
/
lg
n
=
1
> \sqrt {\lg n} > \ln {\ln n} > 2^{\lg^* n} > \lg^* n = \lg^*{(\lg n)} > \lg {(\lg^* n)} > n^{1/ \lg n} =1
> lg n
> ln ln n > 2 lg ∗ n > lg ∗ n = lg ∗ ( lg n ) > lg ( lg ∗ n ) > n 1 / lg n = 1
b.给出非负函数
f
(
n
)
f(n)
f ( n )
(
a
)
(a)
( a )
,
g
i
(
n
)
,
f
(
n
)
,g_i(n),f(n)
, g i ( n ) , f ( n )
O
(
g
i
(
n
)
)
O(g_i(n))
O ( g i ( n ) )
Ω
(
g
i
(
n
)
)
\Omega(g_i(n))
Ω ( g i ( n ) )
b. 非连续性函数或者震荡函数就能满足要求,比如 KaTeX parse error: Expected 'EOF', got '\cases' at position 6: f(n)=\̲c̲a̲s̲e̲s̲ ̲{ n, & $-1^n > … 或
(
2
2
2
n
+
1
)
s
i
n
x
\LARGE(2^{2^{2n+1}})^{sinx}
( 2 2 2 n + 1 ) s i n x
假设
f
(
n
)
f(n)
f ( n )
g
(
n
)
g(n)
g ( n )
a.
f
(
n
)
=
O
(
g
(
n
)
)
f(n)=O(g(n))
f ( n ) = O ( g ( n ) )
g
(
n
)
=
O
(
f
(
n
)
)
g(n)=O(f(n))
g ( n ) = O ( f ( n ) )
错误。反例:
n
=
O
(
n
2
)
n=O(n^2)
n = O ( n 2 )
n
2
≠
O
(
n
)
n^2 \ne O(n)
n 2 ̸ = O ( n )
b.
f
(
n
)
+
g
(
n
)
=
Θ
(
min
(
f
(
n
)
,
g
(
n
)
)
)
f(n)+g(n)=\Theta(\min(f(n),g(n)))
f ( n ) + g ( n ) = Θ ( min ( f ( n ) , g ( n ) ) )
错误。反例:
n
+
n
2
≠
Θ
(
min
(
n
,
n
2
)
)
=
Θ
(
n
)
n+n^2\ne \Theta(\min (n, n^2)) =\Theta(n)
n + n 2 ̸ = Θ ( min ( n , n 2 ) ) = Θ ( n )
c.
f
(
n
)
=
O
(
g
(
n
)
)
f(n)=O(g(n))
f ( n ) = O ( g ( n ) )
lg
(
f
(
n
)
)
=
O
(
lg
(
f
(
n
)
)
)
\lg(f(n))=O(\lg(f(n)))
lg ( f ( n ) ) = O ( lg ( f ( n ) ) )
n
n
n
lg
(
g
(
n
)
)
≥
1
\lg(g(n))\ge 1
lg ( g ( n ) ) ≥ 1
f
(
n
)
≥
1
f(n)\ge1
f ( n ) ≥ 1
正确。
f
(
n
)
≥
1
f(n)\ge1
f ( n ) ≥ 1
f
(
n
)
=
O
(
g
(
n
)
)
f(n)=O(g(n))
f ( n ) = O ( g ( n ) )
c
,
n
0
>
0
c,n_0>0
c , n 0 > 0
n
>
n
0
n>n_0
n > n 0
0
≤
f
(
n
)
≤
c
g
(
n
)
⇒
0
≤
lg
f
(
n
)
≤
lg
(
c
g
(
n
)
)
=
lg
c
+
lg
g
(
n
)
0 \leq f(n) \leq cg(n) \Rightarrow 0 \leq \lg{f(n)} \leq \lg(cg(n)) = \lg{c} + \lg{g(n)}
0 ≤ f ( n ) ≤ c g ( n ) ⇒ 0 ≤ lg f ( n ) ≤ lg ( c g ( n ) ) = lg c + lg g ( n )
因为
lg
(
g
(
n
)
)
≥
1
\lg(g(n))\ge1
lg ( g ( n ) ) ≥ 1
c
′
=
lg
c
+
1
c'=\lg{c} +1
c ′ = lg c + 1
n
0
′
n_0'
n 0 ′ KaTeX parse error: No such environment: align at position 7: \begin{̲a̲l̲i̲g̲n̲}̲ \lg{f(n)} &\le…
即有
lg
(
f
(
n
)
)
=
O
(
l
g
(
g
(
n
)
)
)
\lg(f(n)) = O(lg(g(n)))
lg ( f ( n ) ) = O ( l g ( g ( n ) ) )
d.
f
(
n
)
=
O
(
g
(
n
)
)
f(n)=O(g(n))
f ( n ) = O ( g ( n ) )
2
f
(
n
)
=
O
(
2
g
(
n
)
)
2^{f(n)}=O(2^{g(n)})
2 f ( n ) = O ( 2 g ( n ) )
错误。反例:
2
n
=
O
(
n
)
2n = O(n)
2 n = O ( n )
2
2
n
=
4
n
≠
O
(
2
n
)
2^{2n} = 4^n \neq O(2^n)
2 2 n = 4 n ̸ = O ( 2 n )
e.
f
(
n
)
=
O
(
(
f
(
n
)
)
2
)
f(n)=O((f(n))^2)
f ( n ) = O ( ( f ( n ) ) 2 )
,
n
>
n
0
,
f
(
n
)
≥
1
,n>n_0,f(n)\ge 1
, n > n 0 , f ( n ) ≥ 1
f
(
n
)
≤
c
f
(
n
)
≤
c
(
f
(
n
)
)
2
f(n)\le cf(n)\le c(f(n))^2
f ( n ) ≤ c f ( n ) ≤ c ( f ( n ) ) 2
f.
f
(
n
)
=
O
(
g
(
n
)
)
f(n)=O(g(n))
f ( n ) = O ( g ( n ) )
g
(
n
)
=
Ω
(
f
(
n
)
)
g(n)=\Omega(f(n))
g ( n ) = Ω ( f ( n ) )
正确。
0
≤
f
(
n
)
≤
c
g
(
n
)
⇒
c
g
(
n
)
≥
f
(
n
)
≥
0
⇒
g
(
n
)
≥
(
1
/
c
)
f
(
n
)
≥
0
0\le f(n)\le cg(n)\Rightarrow cg(n)\ge f(n)\ge 0\Rightarrow g(n)\ge (1/c)f(n)\ge 0
0 ≤ f ( n ) ≤ c g ( n ) ⇒ c g ( n ) ≥ f ( n ) ≥ 0 ⇒ g ( n ) ≥ ( 1 / c ) f ( n ) ≥ 0
g.
f
(
n
)
=
Θ
(
f
(
n
/
2
)
)
f(n)=\Theta(f(n/2))
f ( n ) = Θ ( f ( n / 2 ) )
错误。反例:
2
n
=
Θ
(
2
n
)
=
ω
(
2
n
/
2
)
2^n = \Theta(2^n) = \omega(2^{n/2})
2 n = Θ ( 2 n ) = ω ( 2 n / 2 )
h.
f
(
n
)
+
o
(
f
(
n
)
)
=
Θ
(
f
(
n
)
)
f(n)+o(f(n))=\Theta(f(n))
f ( n ) + o ( f ( n ) ) = Θ ( f ( n ) )
正确,
g
(
n
)
=
o
(
f
(
n
)
)
g(n)=o(f(n))
g ( n ) = o ( f ( n ) )
n
0
n_0
n 0
c
c
c
n
≥
n
0
n \ge n_0
n ≥ n 0
g
(
n
)
<
f
(
n
)
g(n) < f(n)
g ( n ) < f ( n )
n
≥
n
0
n \ge n_0
n ≥ n 0
f
(
n
)
+
o
(
f
(
n
)
)
)
<
f
(
n
)
+
f
(
n
)
=
2
f
(
n
)
f(n)+o(f(n))) < f(n) + f(n) = 2f(n)
f ( n ) + o ( f ( n ) ) ) < f ( n ) + f ( n ) = 2 f ( n )
O
O
O
Ω
\Omega
Ω
某些作者用一种与我们稍微不同的方式来定义
Ω
\Omega
Ω
Ω
∞
\overset{\infty}{\Omega}
Ω ∞
Ω
\Omega
Ω
c
c
c
n
n
n
f
(
n
)
≥
c
g
(
n
)
≥
0
f(n)\ge cg(n)\ge 0
f ( n ) ≥ c g ( n ) ≥ 0
f
(
n
)
=
Ω
∞
(
g
(
n
)
)
f(n) =\overset{\infty}{\Omega}(g(n))
f ( n ) = Ω ∞ ( g ( n ) )
a.证明:对渐近非负的任意两个函数
f
(
n
)
f(n)
f ( n )
g
(
n
)
g(n)
g ( n )
f
(
n
)
=
O
(
g
(
n
)
)
f(n)=O(g(n))
f ( n ) = O ( g ( n ) )
f
(
n
)
=
Ω
∞
(
g
(
n
)
)
f(n)=\overset{\infty}{\Omega}(g(n))
f ( n ) = Ω ∞ ( g ( n ) )
Ω
\Omega
Ω
Ω
∞
\overset{\infty}{\Omega}
Ω ∞
反例:
n
=
Ω
∞
(
n
sin
n
)
n = \overset{\infty}{\Omega}(n^{\sin{n}})
n = Ω ∞ ( n sin n )
n
≠
Ω
(
n
sin
n
)
n \neq \Omega(n^{\sin{n}})
n ̸ = Ω ( n sin n )
Ω
∞
\overset{\infty}{\Omega}
Ω ∞
b.描述用
Ω
∞
\overset{\infty}{\Omega}
Ω ∞
Ω
\Omega
Ω
优点:
Ω
∞
\overset{\infty}{\Omega}
Ω ∞
某些作者也用一种稍微不同的方式来定义
O
O
O
O
′
O'
O ′
f
(
n
)
=
O
′
(
g
(
n
)
)
f(n)=O'(g(n))
f ( n ) = O ′ ( g ( n ) )
∣
f
(
n
)
∣
=
O
(
g
(
n
)
)
|f(n)|=O(g(n))
∣ f ( n ) ∣ = O ( g ( n ) )
c.如果使用
O
′
O'
O ′
O
O
O
Ω
\Omega
Ω
O
′
O'
O ′
f
(
n
)
≥
c
g
(
n
)
f(n)\ge cg(n)
f ( n ) ≥ c g ( n )
∣
f
(
n
)
∣
≥
c
g
(
n
)
|f(n)|\ge cg(n)
∣ f ( n ) ∣ ≥ c g ( n )
∣
f
(
n
)
∣
≥
c
g
(
n
)
|f(n)|\ge cg(n)
∣ f ( n ) ∣ ≥ c g ( n )
f
(
n
)
≥
c
g
(
n
)
f(n)\ge cg(n)
f ( n ) ≥ c g ( n )
有些作者定义KaTeX parse error: Expected group after '\tilde' at position 7: \tilde\̲O̲ (读作“软O”)来意指忽略对数因子的
O
O
O
KaTeX parse error: Expected '}', got '\O' at position 21: …和,使得对所有有\tilde{\̲O̲}(g(n))=\{f(n):…
d.用一种类似的方式定义
Ω
~
\tilde{\Omega}
Ω ~
Θ
~
\tilde{\Theta}
Θ ~
KaTeX parse error: Expected 'EOF', got '\eqalign' at position 3: 对有\̲e̲q̲a̲l̲i̲g̲n̲ ̲{ \tilde \Omega… KaTeX parse error: Expected 'EOF', got '\eqalign' at position 3: 对有\̲e̲q̲a̲l̲i̲g̲n̲ ̲{ \tilde \Theta… 定理3.1由定义可知。
我们可以把用于
lg
∗
\lg^*
lg ∗
∗
*
∗
f
(
n
)
f(n)
f ( n )
c
∈
R
c\in \mathbb{R}
c ∈ R
f
c
∗
f_c^*
f c ∗
f
c
∗
(
n
)
=
min
{
i
≥
0
:
f
(
i
)
(
n
)
≤
c
}
f_c^*(n)=\min\{i\ge0:f^{(i)}(n)\le c\}
f c ∗ ( n ) = min { i ≥ 0 : f ( i ) ( n ) ≤ c }
f
c
∗
(
n
)
f_c^*(n)
f c ∗ ( n )
c
c
c
f
f
f
f
(
n
)
f(n)
f ( n )
c
c
c
f
c
∗
(
n
)
f_c^*(n)
f c ∗ ( n )
f
(
n
)
f(n)
f ( n )
c
c
c
f
c
∗
(
n
)
f^∗_c(n)
f c ∗ ( n )
n
−
1
n−1
n − 1
0
0
0
Θ
(
n
)
\Theta(n)
Θ ( n )
lg
n
\lg n
lg n
1
1
1
Θ
(
lg
∗
n
)
\Theta(\lg^∗n)
Θ ( lg ∗ n )
n
/
2
n/2
n / 2
1
1
1
Θ
(
lg
n
)
\Theta(\lg n)
Θ ( lg n )
n
/
2
n/2
n / 2
2
2
2
Θ
(
lg
n
)
\Theta(\lg n)
Θ ( lg n )
n
\sqrt n
n
2
2
2
Θ
(
lg
lg
n
)
\Theta(\lg \lg n)
Θ ( lg lg n )
n
\sqrt n
n
1
1
1 无法收敛
n
1
/
3
n^{1/3}
n 1 / 3
2
2
2
Θ
(
log
3
lg
n
)
\Theta(\log_3\lg n)
Θ ( log 3 lg n )
n
/
lg
n
n/\lg n
n / lg n
2
2
2
ω
(
l
g
l
g
n
)
,
o
(
l
g
n
)
\omega(lglgn),o(lgn)
ω ( l g l g n ) , o ( l g n )
f
(
n
)
=
n
f(n)=\sqrt n
f ( n ) = n
KaTeX parse error: No such environment: align at position 7: \begin{̲a̲l̲i̲g̲n̲}̲ {{{n^{\frac{1}…
f
(
n
)
=
n
/
lg
n
f(n)=n/\lg{n}
f ( n ) = n / lg n
n
n
n
n
/
n
<
n
/
lg
n
<
n
/
2
n / \sqrt{n} < n/\lg{n} < n/2
n / n
< n / lg n < n / 2

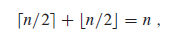
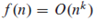 ,则称函数
为多项式有界的。
,则称函数
为多项式有界的。