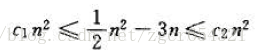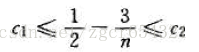Θ记号:
该记号圆圈中是个M。Θ记号渐近地给出一个函数的上界和下界。
对于一个给定的函数g(n),我们用Θ(g(n))来表示以下函数的集合:
Θ(g(n))={f(n):存在正常量c1、c2和n0,使得对于所有n⩾n0,有0⩽c1g(n)⩽f(n)⩽c2g(n)}。
即若存在正常量c1和c2,使得对于足够大的n,f(n)能够夹入c1g(n)和c2g(n)之间,则f(n)属于集合Θ(g(n))。对在n0及其右边的所有值,函数f(n)在一个常量因子内等于g(n),我们称g(n)是f(n)的一个渐近紧确界(asymptotically tight bound)。
Θ(g(n))的定义要求每个成员f(n)属于Θ(g(n))集合均渐近非负,即当n足够大时,f(n)非负,即要求f(n)为渐近正函数。
引进非正式的Θ记号,其效果相当于舍弃了低阶项和忽略了最高阶项的系数。
如:
使用定义证明: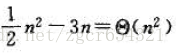
首先要确定正常量c1、c2和n0,使得对于所有n⩾n0,有下式成立:
用n2除上式得:
选择任何常量c1⩽1/14,可以使左边的不等式对任何的n⩾7的值成立。同样的,通过选择任何常量c2⩾1/2,可以使右边的不等式对任何n⩾1都成立。
这样,通过选择c1=1/14,c2=1/2,n0=7,可以证明12n2−3n=Θ(n2)。
O记号:
O记号给出一个函数的渐近上界。
对于给定的函数g(n),用O(g(n))来表示以下函数的集合:
O(g(n))={f(n):存在正常量c和n0,使得对所有n⩾n0,有0⩽f(n)⩽cg(n)}。
O记号为函数给出一个在常量因子内的上界,如果存在正常量c和n0,使得在n0及其右边,f(n)的值总小于或等于cg(n),那么记f(n)=O(g(n))。
Ω记号:
Ω记号给出一个函数的渐近下界。
对于给定的函数g(n),用Ω(g(n))来表示以下函数的集合:
Ω(g(n))={f(n):存在正常量c和n0,使得对所有n⩾n0,有0⩽cg(n)⩽f(n)}。
Ω记号为函数给出一个在常量因子内的下界,如果存在正常量c和n0,使得在n0及其右边,f(n)的值总大于或等于cg(n),那么记f(n)=Ω(g(n))。
定理3.1:
对于任意的两个函数f(n)和g(n),我们有f(n)=Θ(g(n)),当且仅当f(n)=O(g(n))且f(n)=Ω(g(n))。
等式和不等式中的渐近记号:
一般来说,当渐近记号出现在某个公式中,我们将其解释为代表某个我们不关注名称的匿名函数。
如:
公式2n2+3n+1=2n2+Θ(n)指2n2+3n+1=2n2+f(n),其中f(n)是集合Θ(n)中的某个函数。一个表达式中匿名函数的数目可以理解为等于渐近记号出现的次数。
渐近记号的这种用法有助于略去一个等式中无关紧要的细节。
如:
合并排序的最坏情况运行时间递归式为:
如果仅对T(n) 的渐近行为感兴趣,则没有必要写出所有低阶项,它们都被包含在由Θ(n) 表示的匿名函数中了。
o记号:
我们使用o记号来表示一个非渐近紧确的上界。
形式化地定义o(g(n))为以下集合:o(g(n))={f(n):对任意正常量c>0,存在常量n0>0,使得对所有n⩾n0,有0⩽f(n)<cg(n)}。
O记号与o记号主要的区别是在f(n)=O(g(n))中,界0⩽f(n)⩽cg(n)对某个常量c>0成立,但在f(n)=o(g(n))中,界0⩽f(n)<cg(n)对所有常量c>0成立。直观上,在o记号中,当n趋于无穷时,函数f(n)相对于g(n)来说变得微不足道了。
ω记号:
我们使用ω记号来表示一个非渐近紧确的下界。
ω记号的定义为:f(n)∈ω(g(n))当且仅当g(n)∈o(f(n))。
形式化定义ω(g(n))为以下集合:ω(g(n))={f(n):对任意正常量c>0,存在常量n0>0,使得对所有n⩾n0,有0⩽cg(n)<f(n)}。
直观上,当n趋于无穷时,f(n)相对于g(n)来说变得任意大了。
渐近记号的性质:
传递性:
f(n)=Θ(g(n))且g(n)=Θ(h(n)) 蕴涵f(n)=Θ(h(n))
f(n)=O(g(n))且g(n)=O(h(n)) 蕴涵f(n)=O(h(n))
f(n)=Ω(g(n))且g(n)=Ω(h(n)) 蕴涵f(n)=Ω(h(n))
f(n)=o(g(n))且g(n)=o(h(n)) 蕴涵f(n)=o(h(n))
f(n)=ω(g(n))且g(n)=ω(h(n)) 蕴涵f(n)=ω(h(n))
自反性 :
f(n)=Θ(f(n))
f(n)=O(f(n))
f(n)=Ω(f(n))
对称性:
f(n)=Θ(g(n))当且仅当g(n)=Θ(f(n))
转置对称性:
f(n)=O(g(n))当且仅当g(n)=Ω(f(n))
f(n)=o(g(n))当且仅当g(n)=ω(f(n))
f(n)=O(g(n)类似于a⩽b
f(n)=Ω(g(n)类似于a⩾b
f(n)=Θ(g(n)类似于a=b
f(n)=o(g(n))类似于a<b
f(n)=ω(g(n))类似于a>b
若f(n)=o(g(n)),则称f(n)渐近小于g(n);若f(n)=ω(g(n)),则称f(n)渐近大于g(n)。
对于任意两个实数a和b,必然存在a<b、a>b、a=ba<b、a>b、a=b三者之一成立,称为实数的三分性;而对于渐近符号,则不存在三分性。
习题:
3.1-1:
设f(n)与g(n)都是渐近非负函数。利用记号的基本定义来证明
题目即要证明存在正常数c1,c2,n0;使对于所有n>=n0,有0 <= c1(f(n)+g(n)) <= max(f(n),g(n))<=c2(f(n)+g(n))
因为f(n)+g(n) <= 2max(f(n),g(n))
所以1/2(f(n)+g(n)) <= max(f(n),g(n))
又因为f(n)和g(n)都均非负,
所以max(f(n),g(n)) <= (f(n)+g(n))
所以1/2(f(n)+g(n)) <= max() <= f(n)+g(n)
所以存在正常数c1=1/2,c2=1, n0=0对所有n>0都有有c1(f(n)+g(n)) <= max(f(n),g(n))<=c2(f(n)+g(n)),得证。
3.1-2:
证明对任意实常数a和b,其中b>0,有
因为n+a <= n+|a|
所以当|a| <= n时,n+a <= 2n
因为n+a >= n-|a|
所以当|a| <= n/2时, n-|a| >= n/2
所以n+a >= n/2
综上可得当n >= 2|a|时,0 < n/2 <= n+a <= 2n
又因为b>0,所以当底数x为正实数时,为单调增函数。故得证。