算法导论 第一部分 第三章-函数的增长

算法导论 第三章-函数的增长

当输入规模大到使只有运行时间的增长量级有关时，就是在研究算法的渐近效率。
我们关心输入规模的无限增长时，在极限中，算法的运行时间如何随着输入规模的变大而增加。
对不是很小的输入规模来说，渐近的更有效的算法是最好的选择。

渐近记号实际上应用于函数，通常刻画算法的运行时间，也可以刻画算法的其他方面，比如算法的空间数量。

数学知识补充

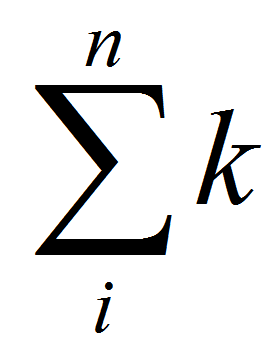
其中i表示下界，n表示上界， k从i开始取数，一直取到n，全部加起来

Θ 记号

对于一个给定函数g(n)，用Θ(g(n))来表示函数集合

Θ(g(n)) = {
    
    
  f(n) 存在正常数c1 c2 n0 ，使对所有n >= n0， 有 0 <= c1*g(n) <= f(n)  <= c2*g(n)  
}

对于任意一个函数f(n)，存在正常数c1 c2，当n充分大时，f(n)能夹在 c1g(n) 和 c2g(n) 之间，
f(n) 属于集合 Θ(g(n))。
f(n) ∈ Θ(g(n))，通常认为 f(n) 就是 Θ(g(n))
对于所有在n0右边的n，f(n)的值总是在c1g(n) 和 c2g(n) 之间。
换句话说，对所有的n>=n0，f(n)在一个常因子范围内与g(n)相等。
我们说 g(n)是f(n)的一个 *** 渐近确界(渐近紧确界) ***

以后，都假设Θ记号中的函数，都是 渐近非负。

证明1

使用形式化定义证明 n2/2 - 3n = Θ(n2)
因此我们要确定常量c1、c2、n0
使得对所有 n>= n0
使得 c1*n2 <= n2/2 -3n <= c2*n2
由上，除以 n2
得到 c1 <= 1/2 - 3/n <= 3n c2
由此可得到任意 c2 >= 1/2 可以让右边成立
c1 <= 1/14 可以让 n>= 7 成立
最后，选择 c1 = 1/14 c2 = 1/2 n0=7 可以成立

使用反证法可以证明 6*n3 !== Θ(n2)

Ο 记号

Ο 读作 奥米克容
我们使用O记号给出函数在一个常量因子内的 渐近上界

Ο(g(n)) = {
    
    
  f(n) 存在正常数c、n0 ，使对所有n >= n0， 有 0 <= f(n) <= c*g(n)
}

那么记做 f(n)=Ο(g(n)) 指 f(n)是集合 Ο(g(n)) 的成员。

注意 f(n) = Θ(g(n)) 包含着 f(n) =Ο(g(n))
Θ记号是比 Ο更强的概念，
对于一个函数，对Θ(n2)的证明，也证明了Ο(n2)
在书中，f(n) = Ο(g(n))，我们仅仅要求g(n)的某个常量倍数是f(n)的渐近上界，但在算法文献中，
要区分渐近上界和渐近确界
使用Ο符号，可以通过检查算法的总体结构来描述算法的运行时间。
例如插入排序双重嵌套循环结构最坏情况运行时间，会产生一个Ο(n2)的上界。

当我们说运行时间是Ο(n2)，指存在一个Ο(n2)的函数f(n)， 对于n的任意值，运行时间的上界都是f(n)，
也就是说最坏情况运行时间是Ο(n2)

Ω记号

Ω记号提供了 渐近下界
对于给定的函数g(n)，用Ω(g(n))表示以下函数的集合。

Ω(g(n)) = {
    
    
  f(n) 存在正常数c、n0 ，使对所有n >= n0， 有 0  <= c*g(n) <= f(n)   
}

那么记做 f(n)= Ω(g(n))

定理

对于任意两个函数f(n)和g(n)， 我们有f(n) = Θ(g(n))，并且仅当 f(n) = Ο(g(n))且f(n) = Ω(g(n))

我们用该定理，是从渐近确界来获得渐近上界和下界，而不是相反。

当称一个算法的运行时间是Ω(g(n))时，我们是指对任意的输入n，
只要n足够大，对那个输入的运行时间至少是g(n)的常量倍。
例如插入排序的最好情况是Ω(n)，所以插入排序的运行时间是Ω(n)到 Ο(n2)。

等式和不等式中的渐近记号

2n2+3n+1 = 2n2+Θ(n)

n=Θ(n2) 等号是指集合的成员关系 n ∈ Θ(n2)

一般，渐近记号出现在公式中，代表不关注名称的匿名函数。
2n2+3n+1 = 2n2+Θ(n)是指2n2+3n+1 = 2n2+f(n)
其中f(n)是集合Θ(n)的某个函数。

*** 无论怎么选择左边的匿名函数，总有一种方法来选择等号右边的匿名函数使等式成立。***
比如

2n2+Θ(n)= Θ(n2)

我们指，对任何函数f(n) ∈ Θ(n)，存在某个函数 g(n) ∈ Θ(n2)，使得对所有的n，有2n2+f(n) = g(n)
换句话说，等式右边的比左边的提供的细节更模糊。

2n2+3n+1 = 2n2+Θ(n)= Θ(n2)

第一个等式，表明存在某个函数 f(n) ∈ Θ(n)，使得对所有的n，有2n2+3n+1 = 2n2+f(n)
第二个等式，表明存在某个函数 g(n) ∈ Θ(n)，存在某个函数 h(n) ∈ Θ(n2)，使得对所有的n，有2n2+g(n)=h(n)

ο记号

ο 来表示一个非渐近紧确的上界。

ο(g(n)) = {
    
    
  f(n) 对任意正常量 n > 0, 存在常量 n0 > 0, 使得对所有的 n>=n0,有 0 <= f(n) < cg(n) 
}

ο 和 Ο 的区别是，f(n) = ο(g(n)) 中， 界0 <= f(n) < cg(n) 对所有的c都成立。

ω

ω 来表示一个非渐近紧确的下界、

ω(g(n)) = {
    
    
  f(n) 对任意正常量 c > 0, 存在常量 n0 > 0, 使得对所有的 n>=n0,有 0 <= cg(n) < f(n) 
}

例如 n2 = ω(n)，关系f(n) = ω(g(n)) 蕴含着

lim 	f(n)
n→∞	 ----  = ∞
      g(n)

函数的比较

假定 f(n)和 g(n) 渐近为正

传递性

f(n)=Θ(g(n))且g(n) = Θ(h(n)),蕴含f(n) = Θ(h(n));
f(n)=Ο(g(n))且g(n) = Ο(h(n)),蕴含f(n) = Ο(h(n));
f(n)=Ω(g(n))且g(n) = Ω(h(n)),蕴含f(n) = Ω(h(n));
f(n)=ο(g(n))且g(n) = ο(h(n)),蕴含f(n) = ο(h(n));
f(n)=ω(g(n))且g(n) = ω(h(n)),蕴含f(n) = ω(h(n));

自反性

f(n)=Θ(f(n))
f(n)=Ο(f(n))
f(n)=Ω(f(n))

对称性

f(n)=Θ(g(n)) 并且仅当 g(n)=Θ(f(n))

转置对称性

f(n)=Ο(g(n)) 并且仅当 g(n)=Ω(f(n))
f(n)=ο(g(n)) 并且仅当 g(n)=ω(f(n))

因为这些性质对渐近记号成立，所以可以在函数f和g的渐近比较和两个实数a和b之间做一个比较。
f(n)=Θ(g(n)) 类似 a = b
f(n)=Ο(g(n)) 类似 a<= b
f(n)=Ο(g(n)) 类似 a>= b
f(n)=ο(g(n)) 类似 a < b
f(n)=ω(g(n)) 类似 a > b
如果 f(n)=ο(g(n))，那么f(n)渐近小于g(n)

三分性

任意两个实数a和b，三种情况之一必成立，a > b , a = b, a < b ;
虽然两个实数可以比较，但并不是所有的函数可以渐近比较。

习题1

如果f(n) 和 g(n) 都是渐近非负函数
证明 max(f(n), g(n)) = Θ(f(n) + g(n))

定义 
f(n) = Θ(g(n))
存在正实数 c1,c2,n0, 使得对所有 n>= n0, 有 c1*g(n) <= f(n) <= c1*g(n) 


假定存在n1 和 n2使得，对所有的n > n1, f(n) >=0, 对所有的n > n2, g(n) >=0,
假定 n0 = max(n1, n2),对于 n > n0 

f(n) <= max(f(n),g(n)) 
g(n) <= max(f(n),g(n)) 

上述相加，得到 
(f(n)+ g(n))/2 <= max(f(n),g(n));
同时 
max(f(n),g(n)) < f(n)+ g(n)
综上,所有对 n > n0 
0 <= (f(n)+ g(n))/2 < max(f(n),g(n)) < f(n)+ g(n) 就是定义 c1 = 1/2 c2 = 1 

标准记号和常用函数

单调性

m <= n, f(m) <= f(n) 单调递增
m <= n, f(m) >= f(n) 单调递减
m < n, f(m) < f(n) 严格递增
m < n, f(m) > f(n) 严格递减

向上取整和向下取整

⌊x⌋ 是小于等于x的最大整数
x - 1 < 　⌊x⌋ <= x <= ⌈x⌉ < x +1

模运算

任意正整数a和n，a mod n 就是a除以n的余数。
a mod n = a - n * ⌊a/n⌋
结果 0 <= a mod n < n
如果a和b除以n有相同的余数，那么 a===b(mod n)

多项式

对一个非负整数d，n的d次多项式，为以下函数

		d
p(n) =  Σ a(i)* n^i
		i
其中ai是常数，对于一个d次渐近多项式p(n) = Θ(n^d)

如果对某个常量k，f(n) = Ο(n^k), 则称函数f(n)是多项式有界的。

指数

a ⁰ = 1
a ^a = a
a ^-1 = 1/a
(a ^m)ⁿ = a ^mn
a ^ma ⁿ = a ^m+n

// a > 1的实常量a和b

lim   n^b
n→∞	 ----  = 0
      a^n

得到 n^b = ο（aⁿ）
指数函数比多项式函数，增长的快

e表示自然对数函数的底2.7…
e^x = 1 + x + x² / 2! …
得到 e^x >= 1 + x

对数

lgn = log₂n
lnn = log_en
lg^kn=(lgn)^k

a = b ^logba
log_c(ab) = log_ca + log_cb
log_baⁿ = nlog_ba
log_ba = log_ca/log_cb
log_b1/a = -log_ba
log_ba * log_ab = 1

对数的底从一个常量变成另外一个常量仅使对数的值改变的一个常量因子。
我们不关系这些常量因子，比如Ο记号，使用lgn，
因为科学家发现2是对数最自然的底，因为很多算法和数据结构都把一个问题分为两个。

对某个常量k，f(n) = Ο(lg^kn),则称函数f(n)是多对数有界的。

对任意常量a > 0 ,
lg_bn = o(n_a)
因为，任意正的多项式函数，都比任意多对数函数增长的快。

阶乘

n! = n * n -1 …1
lgn! = Θ(nlgn)

多重函数

使用记号f⁽ⁱ⁾(n)表示函数f(n)重复i次执行于一个初始值n上，对于非负整数i
f⁽ⁱ⁾(n) = {
n // if i = 0
f(f^(i-1)(n)) // if i > 0
}

比如，如果f(n) = 2n，f⁽ⁱ⁾(n) = 2⁽ⁱ⁾n

多重对数函数

lgn 表示多重对数。
假定lg⁽ⁱ⁾n 定义如上，且f(n) = lg(n)
于是lgn = min{i>=0:lg⁽ⁱ⁾n <=1}
简单的说，使得lg⁽ⁱ⁾ n ≦ 1 的最小i值
多重对数是一个增长非常慢的函数

lg2 = 1
lg4 = 2
lg16 = 3
lg(2¹⁶) = 4
所以很少有 lg^*n > 5 的情况。

斐波那契数

每个斐波那契数都是前两个数之和
它和黄金分割率a和其共轭数b有关
它们是x² = x + 1的两个解。

F_i = (aⁱ - bⁱ)除以 根号5
F_i = ⌊ 1/2 + aⁱ/ 根号5 ⌋

习题

证明 a ^log_bc = c ^log_ba

log_bc = log_ac / log_ab

所以 (a^log_ac )^1/log_ab = c ^log_ba