概念:
泰勒公式是将一个在x=x0处具有n阶导数的函数f(x)利用关于(x-x0)的n次多项式来逼近函数的方法。
若函数f(x)在包含x0的某个闭区间[a,b]上具有n阶导数,且在开区间(a,b)上具有(n+1)阶导数,则对闭区间[a,b]上任意一点x,成立下式:
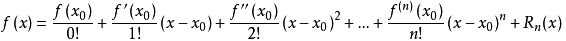
其中,f(n)(x)表示f(x)的n阶导数,等号后的多项式称为函数f(x)在x0处的泰勒展开式,剩余的Rn(x)是泰勒公式的余项,是(x-x0)n的高阶无穷小。
麦克劳林展开
函数的麦克劳林展开指上面泰勒公式中x0取0的情况,即是泰勒公式的特殊形式,若f(x)在x=0处n阶连续可导,则下式成立:
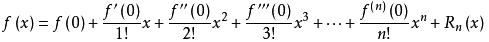
其中f(n)(x)表示f(x)的n阶导数。
泰勒展开的物理意义:
说白了就是一介导数看斜率的变化,二阶导数看趋势是凹形状,还是凸形状,三阶导数趋势的凹凸性变化。。。。。。四阶和五阶等等其实都是看整个函数是否逼近原函数的一个变化情况。
典型的列子:
例1、展开三角函数y=sinx和y=cosx。
解:根据导数表得:
显然y=sinx在x=0处具有任意阶导数,并且
 。
。
根据麦克劳林公式:
类似地,可以展开y=cosx。
例2、当
 时,证明
时,证明
 。
。
证明 :函数
 在
在
 点处的二阶泰勒公式为
点处的二阶泰勒公式为

在
 时,显然成立
时,显然成立
 ,即
,即
 。
。
例3、求极限
 。
。

解: 利用
(1)
 ;
;
(2)
 ;
;
(3)
 ;
;
(4)
 ;
;
可得
 。
。

例4、计算近似值
 ,并估计误差。
,并估计误差。
解:对指数函数
 运用
麦克劳林展开式并舍弃余项:
运用
麦克劳林展开式并舍弃余项:
当x=1时:
取n=10,即可算出近似值e≈2.7182818。
误差为

(其中
 ,即一个
虚数单位)
,即一个
虚数单位)
证明:
由于在实数范围以内,

将该式子扩展到复数系内以定义指数函数,得到
特别地,当上式z=ib时,有
把上面的b换成x,就得到了欧拉公式。
由欧拉公式,对任意一个复数z=a+ib,有
即复数z的指数函数依然是一个复数,这个复数的模r=e
a,幅角θ=b。
若b=0,则e
z=e
a(cos0+isin0)=e
a(1+0)=e
a,与实变函数f(x)=e
x在x=a时的函数值相同
能干什么:
-
幂级数的求导和积分可以逐项进行,因此求和函数相对比较容易。
一个解析函数可被延伸为一个定义在复平面上的一个开片上的解析函数,并使得复分析这种手法可行。
泰勒级数可以用来近似计算函数的值,并估计误差。
证明不等式。
求待定式的极限。
泰勒公式的理解:
地址:https://blog.csdn.net/dog250/article/details/76360262