注：本文针对常用的连续分布：正态分布、均匀分布、指数分布、伽马分布、卡方分布与贝塔分布作了大致的介绍，需要记住它们的参数、数学期望与方差、以及密度函数，一个分布就是一个概率模型。

常用连续分布

1 正态分布 $N\left ( \mu ,\sigma^{2} \right )$

密度函数、分布函数、背景、参数 $\mu$ 、参数 $\sigma$

标准正态分布、标准化变换、由正态分布计算概率值、正态分布的3 $\sigma$ 原则

2 均匀分布 $U\left ( a,b \right )$

背景、密度函数、分布函数、均匀分布的密度函数与分布函数图

期望与方差、标准均匀分布

3 指数分布 $Exp(\lambda)$

背景、密度函数、指数分布密度函数图、分布函数

数学期望与方差、指数分布的无记忆性

4 伽马分布 $Ga\left ( \alpha ,\lambda \right )$

伽马函数、背景、密度函数、数学期望与方差、与指数分布的关系

5 卡方分布 $\chi ^{2}\left ( n \right )$

与伽马分布的关系、密度函数、期望与方差

6 贝塔分布 $Be\left ( \alpha,\beta \right )$

背景、贝塔函数、密度函数、数学期望与方差、与均匀分布的关系

7 常用连续分布表

对数正态分布 $Ln\left ( \mu ,\sigma ^{2} \right )$ 、柯西分布、韦布尔分布

常用连续分布

各种分布之间的关系

伽马分布与指数分布： $Ga\left ( 1,\lambda \right )=Exp\left ( \lambda \right )$
负二项分布与几何分布【离散分布】： $Nb\left ( 1,p \right )= Ge\left ( p \right )$
伽马分布与卡方分布： $Ga\left ( \frac{n}{2} ,\frac{1}{2}\right )=\chi ^{2}(n)$
正态分布与卡方分布：若 $X_{1}, X_{2},...,X_{n}\: \: \textup{i.i.d}\sim N\left ( 0,1 \right )$ ，则 $X= \sum_{i=1}^{n}X_{i}\sim \chi ^{2}\left ( n \right )$
贝塔分布与均匀分布： $Be\left ( 1,1 \right )=U\left ( 0,1 \right )$

1 正态分布 $N\left ( \mu ,\sigma^{2} \right )$

密度函数

$p\left ( x \right )=\frac{1}{\sqrt{2\pi }\sigma }e^{-\frac{\left ( x-\mu \right )^{2}}{2\sigma ^{2}}} \: ;\: -\infty < x< +\infty$

正态分布的密度函数曲线又称“钟形曲线”

分布函数

$F\left ( x \right )=P\left ( X< x \right )=\frac{1}{\sqrt{2\pi }\sigma }\int_{-\infty }^{x}e^{-\frac{\left ( x-\mu \right )^{2}}{2\sigma ^{2}}}\mathrm{d}t\: ,\: -\infty < x< +\infty$

或写成用分号隔开参数和随机变量的形式

$F(x;\mu,\sigma) = \frac{1}{\sigma\sqrt{2\pi}} \int_{-\infty}^x \exp \left( -\frac{(t - \mu)^2}{2\sigma^2} \ \right)\, dt.$

其中参数 $-\infty < \mu < +\infty$ ， $\sigma > 0$

背景:

测量误差常被认为服从正态分布/【高斯分布】，因为它是由大量微小的、独立的随机因素叠加的结果。

参数 $\mu$

$\mu$ 是正态分布的数学期望，即 $E\left ( X \right )=\mu$ ,称 $\mu$ 为正态分布的位置参数/对称中心，以 $x=\mu$ 为对称轴，正态分布左右两边的密度函数曲线 $p\left ( x \right )$ 与x 轴所围的面积各为0.5 ， $\mu$ 也是正态分布的中位数。
标准差 $\sigma$ 相同，而 $\mu$ 不同时，相当于把密度函数曲线 $p\left ( x \right )$ 沿着x轴作水平位移，如下图所示

（图的右上角备注了不同颜色的曲线对应的参数）

若 $X\sim N\left ( \mu ,\sigma ^{2} \right )$ ,则 X在离 $\mu$ 越近取值的可能性越大；离 $\mu$ 越远取值的可能性越小。

参数 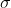$\sigma$

$\sigma ^{2}$ 是正态分布的方差，即 $Var\left ( X \right )=\sigma ^{2}$ ,
$\sigma$ 是正态分布的标准差， $\sigma$ 越小，正态分布越集中，密度曲线越“高瘦”， $\sigma$ 越大，正态分布越分散，密度曲线越“矮胖”， $\sigma$ 又称为正态分布的尺度参数。
若 $X\sim N\left ( \mu ,\sigma ^{2} \right )$ ,则其密度函数 $p\left ( x \right )$ 在 $\mu \pm \sigma$ 处有两个拐点。
设 $X\sim N\left ( 0,\sigma ^{2} \right )$ ,则 $E\left | X \right |=\sigma \sqrt{\frac{2}{\pi }}$

标准正态分布

称 $\mu =0,\sigma =1$ 的正态分布 $N\left ( 0,1 \right )$ 为标准正态分布，记U为标准正态变量，标准正态分布的密度函数 $\varphi \left ( u \right )$ 和分布函数 $\Phi \left ( u \right )$ 满足如下关系：

$\varphi \left ( u \right )=\varphi \left ( -u \right )$
$\Phi \left ( -u \right ) =1-\Phi \left ( u \right )$ ；对于 $u> 0,\Phi \left ( u \right )$ 的值可直接查正态分布表。

标准化变换

正态分布的性质：正态变量的线性变换仍为正态变量，即

若 $X \sim N\left ( \mu ,\sigma ^{2} \right )$ ，则当 $a\not\equiv 0$ 时，有 $Y= aX+b\sim N\left ( a\mu +b\: ,\: a^{2}\sigma^{2} \right )$ .

若 $X\sim N\left ( \mu ,\sigma ^{2} \right )$ ,则 $U=\frac{\left ( X-\mu \right )}{\sigma }\sim N\left ( 0,1 \right )$ ,其中 $U=\frac{\left ( X-\mu \right )}{\sigma }$ 称为 X的标准化变换。

由正态分布计算概率值

涉及正态分布的概率计算，一般是先转化为标准正态，再查标准正态的分布函数表 $\Phi \left ( u \right )$ ，即可求得概率值。

若 $X\sim N\left ( \mu ,\sigma ^{2} \right )$ ,则对任意的实数a 与b,有

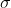$P\left ( X \leqslant b \right )=\Phi \left ( \frac{b-\mu }{\sigma } \right )$
$P\left ( a< X \right )=1- \Phi \left ( \frac{a-\mu }{\sigma } \right )$
$P\left ( a< X \leqslant b \right )=\Phi \left ( \frac{b-\mu }{\sigma } \right ) - \Phi \left ( \frac{a-\mu }{\sigma } \right )$
$\Phi \left ( \frac{1}{2} \right )=0.6915;\Phi \left ( 1 \right )=0.8413;\: \Phi \left ( 2 \right )=0.9972;\: u_{0.95}=1.645;\:$

正态分布的3 $\sigma$ 原则

设 $X\sim N\left ( \mu ,\sigma ^{2} \right )$ ，则

$P\left ( \left | X-\mu \right |< k\sigma \right ) =\Phi (k)-\Phi (-k)=\begin{Bmatrix} 0.6826 \: ,\: k=1 \\ 0.9545\: ,\: k=2 \\ 0.9973\: ,\: k=3 \end{matrix}$

管理学中的六西格玛原则就是与均值 $\mu$ 的标准偏差不小于 6 $\sigma$ ，也就是这种差异的绝对值不小于3 $\sigma$ ，表示当产品质量控制在这个范围内时，此时的产品无缺陷的概率高达99.73%，这个原则可用来降低产品与服务的缺陷次数。参考：六西格玛

后期再讲中心极限定理时，还会再次用到正态分布，它可以说是最基础最重要的连续分布了。

参考正态分布（高斯分布） - hhaowang的博客

2 均匀分布 $U\left ( a,b \right )$

背景

向区间 $\left ( a,b \right )$ 内随机投点，使点落在任意相等长度的小区间内的可能性相等，则落点坐标服从均匀分布 $U\left ( a,b \right )$ .

密度函数

$p( x )= \begin{Bmatrix} 1/\left ( b-a \right )\: ,\: a< x< b \\ 0\: ,\: otherwise \end{matrix}$

分布函数

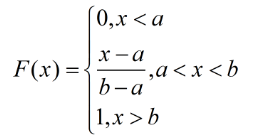
均匀分布的密度函数与分布函数图

期望与方差

$E\left ( X \right )=\frac{a+b}{2}$ ; $Var\left ( X \right ) =\frac{\left ( b-a \right )^{2}}{12}$

标准均匀分布

称区间（0，1）上的均匀分布为标准均匀分布，它是导出其它均匀分布随机数的桥梁。

3 指数分布 $Exp(\lambda)$

背景

很多产品的寿命 可认为（近似）服从指数分布；
一个元器件/设备/系统遇到外来冲击即告失效，则首次冲击来到的时间X(寿命)服从指数分布

密度函数

指数分布密度函数图

分布函数

数学期望与方差

$E\left ( X \right )=\frac{1}{\lambda } \: ;\: Var\left ( X \right ) =\frac{1}{\lambda ^{2}}$

指数分布的无记忆性

若 $X\sim Exp\left ( \lambda \right )$ ，则对任意的 $s> 0,\: t > 0$ ，有 $P\left (X> s+t \: |\: X > s\right ) =P\left ( X> t \right )$

4 伽马分布 $Ga\left ( \alpha ,\lambda \right )$

伽马函数 $\Gamma \left ( \alpha \right )$

称 $\Gamma \left ( \alpha \right ) =\int_{0}^{+\infty }x^{\alpha -1}e^{-x}\mathrm{d}x$ 为伽马函数，其中参数 $\alpha > 0$ ，伽马函数具有如下性质：

$\Gamma \left ( 1 \right )=1$
$\Gamma \left ( \frac{1}{2} \right )=\sqrt{\pi }$
$\Gamma \left ( \alpha +1 \right )=\alpha \Gamma \left ( \alpha \right )$
$\Gamma \left ( n+1 \right )=n \Gamma \left ( n \right )=n! \: ;$ ,n为自然数；或写作 $\Gamma \left ( n \right )=\left ( n-1 \right )!$

余元公式：对于 $x\in \left ( 0,1 \right )$ ,有 $\Gamma \left ( 1-x \right ) \Gamma \left ( x \right )=\frac{\pi }{sin\, \pi x}$

与贝塔函数 $B\left ( m,n \right )$ 的关系 : $B\left ( m,n \right ) =\frac{\Gamma \left ( m \right )\Gamma \left ( n \right )}{\Gamma \left ( m+n \right )}$
对于 $x> 0$ ;伽马函数是严格凹函数。
x足够大时，可以用Stirling 公式来计算Gamma 函数值: $\Gamma \left ( x\right )\sim \sqrt{2\pi }e^{-x}x^{x-\frac{1}{2}}$

背景：

若一个元器件能抵挡一些外来冲击，但遇到第k次冲击即告失效，则第k 次冲击来到的时间X(寿命)服从形状参数为k的伽马分布 $Ga\left ( k,\lambda \right )$ .

密度函数:

$\alpha> 0$ 为形状参数 ， $\lambda > 0$ 为尺度参数 ；

密度函数图如下所示，

数学期望与方差

$E(X)=\frac{\alpha }{\lambda}; Var(X)=\frac{\alpha }{\lambda^{2}}$

与指数分布 $Exp\left ( \lambda \right )$ 的关系

若形状参数为整数k,则伽马变量可以表示成k个独立同分布的指数变量之和。即，

若 $X\sim Ga\left ( k,\lambda \right )$ ,则 $X= X_{1}+X_{2}+\cdots +X_{k}$ ,其中 $X_{i}\sim Exp\left ( \lambda \right ),\: i=1,2,...,k$ 【独立同分布】

5 卡方分布 $\chi ^{2}\left ( n \right )$

与伽马分布的关系

称 $\alpha =\frac{n}{2};\: \lambda =\frac{1}{2}$ 的伽马分布为自由度为n的卡方分布，即 $Ga\left ( \frac{n}{2} ,\frac{1}{2}\right )=\chi ^{2}(n)$

密度函数

期望与方差

$E\left ( X \right )=n;\: Var\left ( X \right )=2n$

注：后期再讲数理统计中的t分布与F分布时，再重新细讲卡方分布。参考重要抽样分布：卡方分布（χ2分布）、t分布和F分布

6 贝塔分布 $Be\left ( \alpha,\beta \right )$

背景

很多比率，比如，产品的不合格率、机器的维修率、某商品的市场占有率、射击的命中率....都是在区间（0，1）上取值的随机变量，可用beta分布来描述这些随机变量

贝塔函数 $B\left ( a,b \right )$

称 $B\left ( a,b \right ) =\int_{0}^{1}x^{a-1}\left ( 1-x \right )^{b-1}\mathrm{d}x$ 为贝塔函数，其中参数 $a> 0,\: b> 0$ 。贝塔函数的性质：

$B\left ( a,b \right )=B\left ( b,a \right )$
$B\left ( a,b \right ) =\frac{\Gamma \left ( a \right )\Gamma \left ( b \right )}{\Gamma \left ( a+b \right )}$

密度函数

当 $0< x< 1$ 时，为f(x);否则为0.

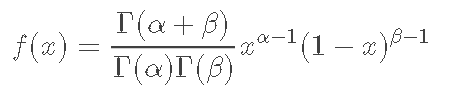
其中 $\alpha > 0 ,\: \beta > 0$ 都是形状参数。【下图中 a就是 $\alpha$ ，b就是 $\beta$ 】

贝塔分布是定义在（0，1）区间上的连续概率分布，是伯努利分布和二项式分布的共轭先验分布。

数学期望与方差

$E\left ( X \right )=\frac{a}{a+b};\: Var\left ( X \right )=\frac{ab}{\left ( a+b \right )^{2}\left ( a+b+1 \right )}$

与均匀分布的关系

当 $a=b=1$ 时的贝塔分布就是区间（0，1）上的均匀分布，即 $Be\left ( 1,1 \right )=U\left ( 0,1 \right )$ .

对数正态分布 $Ln\left ( \mu ,\sigma ^{2} \right )$

若X的密度函数为如下 $f\left ( x;\mu ,\sigma \right )$ ，

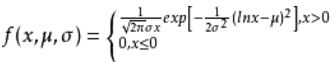
则称X服从对数正态分布，记为 $X\sim Ln\left ( \mu ,\sigma ^{2} \right )$ .其中 $-\infty < \mu < +\infty\: , \: \sigma > 0$ .

对数正态分布的密度函数图

对数正态分布的期望与方差

若 $X\sim Ln\left ( \mu ,\sigma ^{2} \right )$ ，则 $E\left ( X \right )=e^{\mu +\sigma ^{2}/2}\: ,\: Var\left ( X \right )=\left ( e^{\sigma^{2}}-1 \right )e^{2\mu +\sigma ^{2}}$ .

与正态分布的关系：

若 $X\sim Ln\left ( \mu ,\sigma ^{2} \right )$ ，则 $Y=\textup{Ln} \left (X \right )\sim N\left ( \mu ,\sigma ^{2} \right )$

柯西分布、

韦布尔分布

这里写图片描述

7 常用连续分布表

概率论与数理统计教程-茆诗松-第二版；习题与解答

贝塔、伽马分布 - CSDN博客

概率论与数理统计基础（三）:常用连续分布

常用连续分布

各种分布之间的关系

1 正态分布

密度函数

分布函数

背景:

参数

参数

标准正态分布

标准化变换

由正态分布计算概率值

正态分布的3原则

2 均匀分布

背景

密度函数

分布函数

均匀分布的密度函数与分布函数图

期望与方差

;

标准均匀分布

3 指数分布

背景

密度函数

指数分布密度函数图

分布函数

数学期望与方差

指数分布的无记忆性

4 伽马分布

伽马函数

背景：

密度函数:

数学期望与方差

与指数分布 的关系

5 卡方分布

与伽马分布的关系

密度函数

期望与方差

6 贝塔分布

背景

贝塔函数

密度函数

数学期望与方差

与均匀分布的关系

对数正态分布

柯西分布、

韦布尔分布

7 常用连续分布表

猜你喜欢

1 正态分布 $N\left ( \mu ,\sigma^{2} \right )$

参数 $\mu$

参数 $\sigma$

正态分布的3 $\sigma$ 原则

2 均匀分布 $U\left ( a,b \right )$

$E\left ( X \right )=\frac{a+b}{2}$ ; $Var\left ( X \right ) =\frac{\left ( b-a \right )^{2}}{12}$

3 指数分布 $Exp(\lambda)$

4 伽马分布 $Ga\left ( \alpha ,\lambda \right )$

伽马函数 $\Gamma \left ( \alpha \right )$

与指数分布 $Exp\left ( \lambda \right )$ 的关系

5 卡方分布 $\chi ^{2}\left ( n \right )$

6 贝塔分布 $Be\left ( \alpha,\beta \right )$

贝塔函数 $B\left ( a,b \right )$

对数正态分布 $Ln\left ( \mu ,\sigma ^{2} \right )$