逆元， 组合数取模，费马小定理

费马小定理(Fermat’s little theorem)

是数论中的一个重要定理，若p是一个质数，而整数a不是p的倍数有a^（p-1）≡1（mod p）, 理解为若a和p互素且p为质数， 满足a^（p-1）≡1（mod p）。

定理先放这， 现在目标是求

一般的可以做如下转换

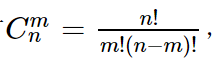
但是取模对除法不适用故

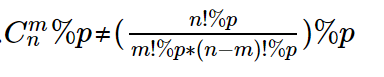
逆元：对于a和p（a和p互素），若a*b%p≡1，则称b为a%p的逆元。

应用:t / a 对 p取模， 由于b是a%p的逆元， t / a 对p取模可以转换为t * b %p 转换为乘法了， 乘法对求模是适用的，接下来用这个来求解组合数。

求逆元：a^（p-1）≡1（mod p）即a^（p-2）* a≡1（mod p）, 有a%p的逆元为a^（p-2）

求组合数

对p取模， 即n! 与 m！% p的逆元，（n-m）！%p的逆元的乘积。用f（x） 表示x！，有表达式为f（n）* f（m）^(p-2) * f(n - m) ^ (p -2)对p取模。其中次方可以用快速幂求，而f（x）可以一开始用一个数组保存小于max_num的阶乘， 注意是对p取模的阶乘，加上取模完整的表达式为

((f（n）* f（m）^(p-2)) % p * f(n - m) ^ (p -2))%p

代码实现如下， solve（a，b）实现的是求得从a个中取b个的组合数对mod取模。

#include<iostream>
#include<algorithm>
#include<cstdlib>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<queue>
#include<set>
#include<map>
#include<string>
#include<vector>
#include<stack>
using namespace std;
typedef long long ll;
const int maxn = 100000, mod = 1e9 + 7;
int fac[maxn * 2];

int pow_mod(int a, int b)
{
	int base = a, res = 1;
	while(b)
	{
		if(b & 1) res = (ll) res * base % mod;
		
			base = (ll) base * base % mod;
		b >>= 1;
	}

	return res;
}

int solve(int a, int b)    				//solve()函数求得从a个中取b个的组合数， 对mod取模
{
	int temp = (ll) fac[b] * fac[a - b] % mod;
	int re = (ll)fac[a] * pow_mod(temp, mod - 2) % mod;
	return re;
}

int main()
{
	ios::sync_with_stdio(false);
	int t;
	cin >> t;
	fac[0] = 1;
	for(int i = 1; i <= 200000; i++) fac[i] = (ll)i * fac[i - 1] % mod;
	while(t--)
	{
		int m, n;
		cin >> m >> n;
		cout << (solve(m + n - 1, m) - solve(m + n -1, m - 1) + mod) % mod << endl;
	}
}