深入浅出强化学习笔记（1）

第一讲笔记

• 深度学习如图像识别和语音识别解决的是感知的问题，强化学习解决的是决策的问题
  强化学习基本框架-马尔科夫决策过程（MDP）
  马尔科夫性：系统的下一状态只与当前状态有关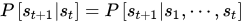
  马尔科夫过程：马尔科夫过程是一个二元组\left(S,P\right)，且满足：S是有限状态集合， P是状态转移概率。状态转移概率矩阵为：
  
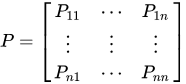
  马尔科夫决策过程：马尔科夫过程中不存在动作和奖励。将动作（策略）和回报考虑在内的马尔科夫过程称为马尔科夫决策过程。

马尔科夫决策过程由元组 $(S,A,P,R,\gamma)$描述，其中：S为有限的状态集, A 为有限的动作集, P 为状态转移概率, R为回报函数, $\gamma$为折扣因子，用来计算累积回报。注意，跟马尔科夫过程不同的是，马尔科夫决策过程的状态转移概率是包含动作的即： $P_{ss'}^{a}=P\left[S_{t+1}=s'|S_t=s,A_t=a\right]$

强化学习的目标：
是给定一个马尔科夫决策过程，寻找最优策略。所谓策略是指状态到动作的映射，策略常用符号\pi 表示，它是指给定状态s 时，动作集上的一个分布，即

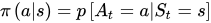
由于策略 $\pi$是随机的，因此累积回报也是随机的。为了评价状态s_1的价值，我们需要定义一个确定量来描述状态 $s_1$的价值，很自然的想法是利用累积回报来衡量状态 $s_1$的价值。然而，累积回报 $G_1$是个随机变量，不是一个确定值，因此无法进行描述。但其期望是个确定值，可以作为状态值函数的定义。

状态值函数：

当智能体采用策略 $\pi$时，累积回报服从一个分布，累积回报在状态s处的期望值定义为状态-值函数：

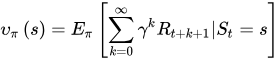
相应地，状态-行为值函数为：

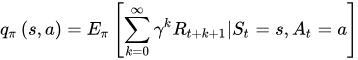
状态值函数与状态-行为值函数的贝尔曼方程

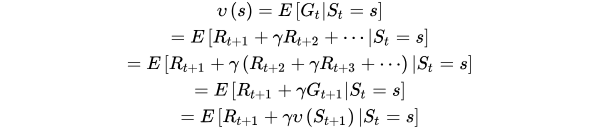
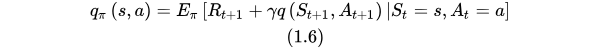
计算过程：a->s->a`(有行动了之后才有 $R_s^a$)

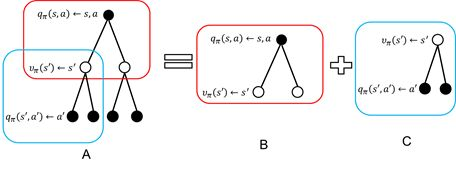
根据策略最优定理知道，当值函数最优时采取的策略也是最优的。反过来，策略最优时值函数也最优。我们就是要max(值函数)

强化学习算法分类：

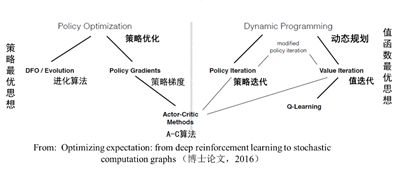
另外：
强化学习算法：
根据策略是否是随机的，分为确定性策略强化学习和随机性策略强化学习。
根据转移概率是否已知可以分为基于模型的强化学习算法和无模型的强化学习算法。
根据回报函数是否已知，可以分为强化学习和逆向强化学习。逆向强化学习是根据专家实例将回报函数学出来。

第二讲笔记：

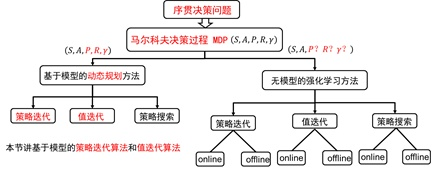
• 利用动态规划可以解决的问题需要满足两个条件：（1）整个优化问题可以分解为多个子优化问题，子优化问题的解可以被存储和重复利用。
• 状态值函数的计算：
  
  状态s处的值函数 ${\upsilon _\pi }\left( s \right)$，可以利用后继状态的值函数 ${\upsilon _\pi }\left( {s'} \right)$来表示。可是有人会说，后继状态的值函数 ${\upsilon _\pi }\left( {s'} \right)$也是不知道的，那怎么计算当前状态的值函数？这不是自己抬起自己吗？如图2.4所示。没错，这正是bootstrapping算法(自举算法)。
  策略评估：
  使用高斯赛德尔进行迭代
  策略改善：
  使用贪婪政策，每步选择值函数最大的那个
  
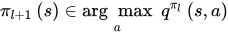
  选择完动作时候，根据动作之后状态的分布，到新的状态
  
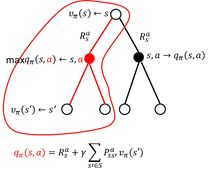
  在这里我们不再强调动作值函数的概念。它是一个过渡。
  策略迭代=策略评估到值函数收敛+策略改善
  值函数迭代=（值函数迭代一次+策略改善一次）x n

第三讲笔记

无模型之蒙特卡罗
无模型强化学习中，模型 $P_{ss'}^{a}$是未知的。
蒙特卡罗方法是利用经验平均代替随机变量的期望。

• 探索策略：

当要评估智能体的当前策略时，我们可以利用策略产生很多次试验，每次试验都是从任意的初始状态开始直到终止状态，比如一次试验(an
episode)为: $S_1,A_1,R_2,\cdots ,S_T$,计算一次试验中状态s处的折扣回报返回值为： $G_t\left(s\right)=R_{t+1}+\gamma R_{t+2}+\cdots +\gamma^{T-1}R_T$

在动态规划方法中，为了保证值函数的收敛性，算法会对状态空间中的状态进行逐个扫描。无模型的方法充分评估策略值函数的前提是每个状态都能被访问到。因此，在蒙特卡洛方法中必须采用一定的方法保证每个状态都能被访问到。其中一种方法是探索性初始化。
在探索性初始化中，迭代每一幕（一个完整过程）时，初始状态是随机分配的，这样可以保证迭代过程中每个状态行为对都能被选中。它蕴含着一个假设，即：假设所有的动作都被无限频繁选中。对于这个假设，有时很难成立，或无法完全保证。
我们会问，如何保证初始状态不变的同时，又能保证报个状态行为对可以被访问到？精心地设计你的探索策略，以保证每个状态都能被访问到。

• 评估策略：
  需要改进并且作为最终结果的策略

根据探索策略（行动策略）和评估的策略是否是同一个策略，蒙特卡罗方法又分为on-policy和off-policy.
On-policy: 同策略是指产生数据的策略与评估和要改善的策略是同一个策略（策略类型）。比如，要产生数据的策略和评估及要改进的策略都是 $\varepsilon -soft$策略。

异策略是指产生数据的策略与评估和改善的策略不是同一个策略。我们用 $\pi$表示用来评估和改进的策略，用 $\mu$表示产生样本数据的策略。
同策略的过程：

异策略可以保证充分的探索性。例如用来评估和改进的策略 $\pi$是贪婪策略，用于产生数据的探索性策略 $\mu$为探索性策略，如 $\varepsilon -soft$策略。

用于异策略的目标策略 $\pi$和行动策略 $\mu$并非任意选择的，而是必须满足一定的条件。这个条件是覆盖性条件即：行动策略 $\mu$产生的行为覆盖或包含目标策略 $\pi$产生的行为。利用式子表示即为：满足 $\pi\left(a|s\right)>0$的任何(s,a) 均满足 $\mu\left(a|s\right)>0$。

利用行为策略产生的数据评估目标策略需要利用重要性采样方法。
重采样
当随机变量z的分布非常复杂时，无法利用解析的方法产生用于逼近期望的样本，这时，我们可以选用一个概率分布很简单，产生样本很容易的概率分布q(z) ，比如正态分布。

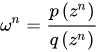
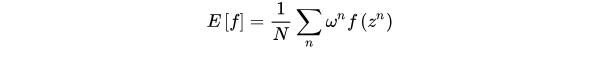
但是被积函数的概率分布往往很难求得，导致采样概率分布和原概率分布的期望一致但是方差较大。
->加权重要性采样

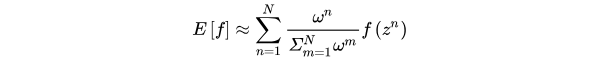
在异策略方法中，行动策略 $\mu$即用来产生样本的策略，所产生的轨迹概率分布相当于重要性采样中的q[z]，用来评估和改进的策略 $\pi$所对应的轨迹概率分布为p[z]，因此利用行动策略 $\mu$所产生的累积函数返回值来评估策略 $\pi$时，需要在累积函数返回值前面乘以重要性权重。
在目标策略 $\pi$下，一次试验的概率为：

$\Pr\left(A_t,S_{t+1},\cdots ,S_T\right)=\prod_{k=t}^{T-1}{\pi\left(A_k|S_k\right)p\left(S_{k+1}|S_k,A_k\right)}$
在行动策略 $\mu$下，相应的试验的概率为：

$Pr\left(A_t,S_{t+1},\cdots ,S_T\right)=\prod_{k=t}^{T-1}{\mu\left(A_k|S_k\right)p\left(S_{k+1}|S_k,A_k\right)}$

因此重要性权重为：

$\rho_{t}^{T}=\frac{\prod_{k=t}^{T-1}{\pi\left(A_k|S_k\right)p\left(S_{k+1}|S_k,A_k\right)}}{\prod_{k=t}^{T-1}{\mu\left(A_k|S_k\right)p\left(S_{k+1}|S_k,A_k\right)}}=\prod_{k=t}^{T-1}{\frac{\pi\left(A_k|S_k\right)}{\mu\left(A_k|S_k\right)}}\\\\\left(3.10\right)$

普通重要性采样，值函数估计为如图3.7所示：

$V\left(s\right)=\frac{\varSigma_{t\in\mathcal{T}\left(s\right)}\rho_{t}^{T\left(t\right)}G_t}{\left|\mathcal{T}\left(s\right)\right|}\\\\\left(3.11\right)$