深入浅出强化学习（4）-IRL

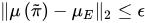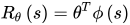
what：
逆向强化学习的提出者Ng是这么想的：专家在完成某项任务时，其决策往往是最优的或接近最优的，那么可以这样假设，当所有的策略所产生的累积回报期望都不比专家策略所产生的累积回报期望大时，强化学习所对应的回报函数就是根据示例学到的回报函数。
定义为从专家示例中学到回报函数。
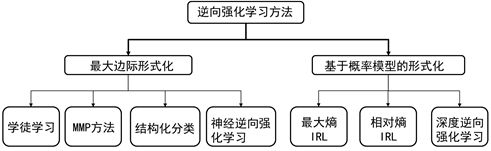
分类：
基于最大边际的逆向强化学习
基于最大熵的方法
具体讲解：
1）
在行为克隆中，人的示例轨迹被记录下来，下次执行时恢复该轨迹。行为克隆的方法只能模仿轨迹，无法进行泛化。而逆向强化学习是从专家（人为）示例中学到背后的回报函数，能泛化到其他情况，因此属于模仿到了精髓。

学徒学习：
找到一个策略，使得该策略的表现与专家策略相近。我们可以利用特征期望来表示一个策略的好坏，找到一个策略，使其表现与专家策略相近，其实就是找到一个策略 $\tilde{\pi}$的特征期望与专家策略的特征期望相近，即使如下不等式成立：

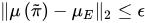
未知的回报函数R(s)一般都是状态的函数，因为它是未知的，所以我们可以利用函数逼近的方法对其进行参数逼近，其逼近形式可设为： $R\left(s\right)=w\cdot\phi\left(s\right)$，其中 $\phi(s)$为基函数，可以为多项式基底，也可以为傅里叶基底。逆向强化学习求的是回报函数中的系数w。
策略 $\pi$的值函数为：

$E_{s_0 ~ D}\left[V^{\pi}\left(s_0\right)\right] \\=E\left[\Sigma_{t=0}^{\infty}\gamma^tR\left(s_t\right)|\pi\right] \\=E\left[\Sigma_{t=0}^{\infty}\gamma^tw\cdot\phi\left(s_t\right)|\pi\right]\\=w\cdot E\left[\Sigma_{t=0}^{\infty}\gamma^t\phi\left(s_t\right)|\pi\right]$
定义特征期望为： $\mu\left(\pi\right)=E\left[\Sigma_{t=0}^{\infty}\gamma^t\phi\left(s_t\right)|\pi\right]$
则，值函数可以写为： $E_{s_0~D}\left[V^{\pi}\left(s_0\right)\right]=w\cdot\mu\left(\pi\right)$
当给定m条专家轨迹后，根据定义我们可以估计专家策略的特征期望为：
$\hat{\mu}_E=\frac{1}{m}\Sigma_{i=1}^{m}\Sigma_{t=0}^{\infty}\gamma^t\phi\left(s_{t}^{\left(i\right)}\right)$
具体计算展开就是：
当该不等式成立时，对于任意的权重\lVert w\rVert_1\le 1，值函数满足如下不等式：

$\left| E\left[\Sigma_{t=0}^{\infty}\gamma^tR\left(s_t\right)|\pi_E\right]-E\left[\Sigma_{t=0}^{\infty}\gamma^tR\left(s_t\right)|\tilde{\pi}\right]\right| \\=\left| w^T\mu\left(\tilde{\pi}\right)-w^T\mu_E\right| \\ \le\lVert w\rVert_2\lVert\mu\left(\tilde{\pi}\right)-\mu_E\rVert_2 \\ \le 1\cdot\epsilon =\epsilon$
写成标准的优化形式为：

[ \max_{t,w} t \s.t.\ w^T\mu_E\geqslant w^T\mu{\left(j\right)}+t,\ j=0,\cdots ,i-1 \\\lVert w\rVert_2\le 1 ]

注意，在进行第二行求解时， $\mu^{\left(j\right)}中的j\in\left\{0,1,\cdots ,i-1\right\}$是前i-1次迭代得到的最优策略。也就是说第i次求解参数时，i-1次迭代的策略是已知的。这时候的最优函数值t相当于专家策略 $\mu_E$与i-1个迭代策略之间的最大边际。

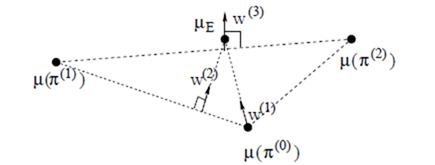
图10.3 最大边际方法的直观理解

如图10.3为最大边际方法的直观理解。我们可以从支持向量机的角度去理解。专家策略为一类，其他策略为另一类，参数的求解其实就是找一条超曲面将专家策略和其他策略区分开来。这个超平面使得两类之间的边际最大。

第四行是在第二行求出参数后，便有了回报函数 $R=\left(w^{\left(i\right)}\right)^T\phi$，利用该回报函数进行强化学习，从而得到该回报函数下的最优策略 $\pi^{\left(i\right)}$。
神经逆向强化学习：
之前，在回报函数的学习过程中，人为引入了基底。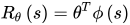
但是人为指定基底，回报函数的表示能力不足，泛化效果不好。
解决：
->使用神经网络作为基底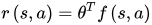
其中f为神经网络.过程使用最大边际法。

2）
背景：
最大熵原理：在学习概率模型时，在所有满足约束的概率模型（分布）中，熵最大的模型是最好的模型。这是因为，通过熵最大所选取的模型，没有对未知（即除了约束已知外）做任何主观假设。
存在一个要潜在的概率分布，在该概率分布下，产生了专家轨迹。这是典型的已知数据，求模型的问题。
也就是说，知道专家轨迹，求解产生该轨迹分布的概率模型。此时，已知条件为：
建模过程：
用 $f$表示特征期望， $\tilde{f}$表示专家特征期望.

该优化问题可形式化为：

$\max-p\log p \\ s.t.\sum_{Path\zeta_i}{P\left(\zeta_i\right)f_{\zeta_i}=\tilde{f}} \\ \varSigma P=1$
利用拉格朗日乘子法，该优化问题可转化为：

$\min\textrm{\ }L=\sum_{\zeta_i}{p\log p-\sum_{j=1}^n{\lambda_j\left(pf_j-\tilde{f}_j\right)}-\lambda_0\left(\varSigma p-1\right)}$

无模型时，使用上诉方法不可。
新方法：
设Q为利用均匀分布策略产生的轨迹分布，要求解的概率分布为P(\tau)，问题可形式化为：

$\min_P\sum_{\tau\in\mathcal{T}}{P\left(\tau\right)\ln\frac{P\left(\tau\right)}{Q\left(\tau\right)}} \\ s.t.for~ all~~ i\in\left\{1,\cdots ,k\right\}\textrm{：} \\ \left|\sum_{\tau\in\mathcal{T}}{P\left(\tau\right)f_{i}^{\tau}-\hat{f}_i}\right|\le\epsilon_i \\ \sum_{\tau\in\mathcal{T}}{P\left(\tau\right)=1} \forall\tau\in\mathcal{T}\ :\ P\left(\tau\right)\geqslant 0$